Raisons trigonométriques Exemples, exercices et applications

Le raisons trigonométriques Ce sont les quotients ou les raisons qui peuvent être faites avec la valeur des côtés d'un triangle droit. Ces côtés sont: deux catégories qui se forment à 90 ° entre elles et l'hypoténuse, qui forme l'angle aigu θ avec l'une des catégories.

6 quotients peuvent être formés. Leurs noms et leurs abréviations respectives sont:

• BRAISE (SEN)
• Coseno (cos)
• tangente (tg ou tan)
• Cotangente (CTG ou Cotan)
• Secante (sec) et
• Harvester (harmonie)

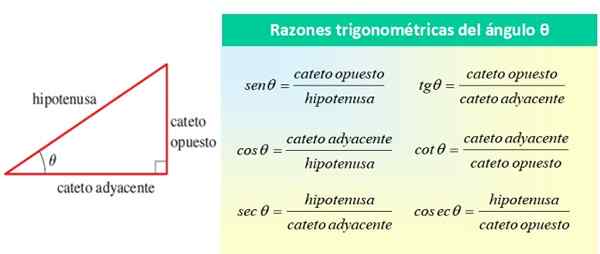
Tous ont fait référence à l'angle θ, comme le montre la figure suivante:

Figure 1. Les raisons trigonométriques de l'angle aigu θ. Source: F. Zapata.

Les raisons trigonométriques de base de l'angle θ sont sin θ, cos θ et tan θ, tandis que les raisons restantes peuvent être exprimées en termes de ces trois. Sur l'image précédente, vous pouvez voir cela:

• Sec θ = 1 / cos θ
• dommage θ = 1 / sin θ
• cot θ = 1 / tg θ

La taille des côtés du triangle n'influence pas la valeur des raisons, car deux triangles dont les angles mesurent les mêmes sont des triangles similaires et les quotients respectifs entre les côtés ont la même valeur.

[TOC]

Exemple

Par exemple, calculons les raisons trigonométriques de l'angle θ dans les triangles suivants:

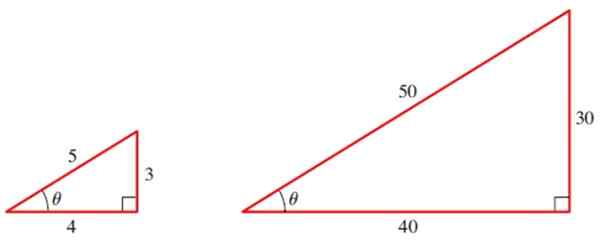Figure 2. Deux triangles similaires ont les mêmes raisons trigonométriques de leurs angles. Source: Stewart, J.Précaulement: mathématiques pour le calcul.

Pour le petit triangle, nous avons les trois raisons de base de l'angle θ:

sin θ = 3/5

cos θ = 4/5

tg θ = ¾

Et maintenant, calculons les trois raisons de base de θ avec le grand triangle:

sin θ = 30/50 = 3/5

cos θ = 40/50 = 4/5

Tg θ = 30/40 = ¾

Un détail important à considérer est le suivant: Sin θ et cos θ sont inférieurs à 1, car les catégories mesurent toujours moins que l'hypoténuse. En effet:

sin θ = 3/5 = 0.6

cos θ = 4/5 = 0.8

Exercices résolus

Dans les exercices suivants, il est invité à résoudre le triangle droit, ce qui signifie trouver la longueur de ses trois côtés et la mesure de ses angles internes, dont l'un mesure toujours 90º.

Peut vous servir: Équations de première dedexes: formule, comment les résoudre, exemple, exercices

Le théorème de Pythagore s'applique aux triangles rectangulaires et est très utile lorsque deux des côtés sont connus et que les manquants doivent être déterminés. Le théorème dit:

Hypoténuse² = Cateto opposé² + cateto adjacent²

Nous pouvons vérifier le théorème de Pythagore avec le petit triangle de la figure 2, dont les jambes sont 3 et 4. L'ordre dans lequel les catégories sont prises n'ont pas d'importance. Appliquer le théorème que nous avons:

Hypoténuse² = 3² + 4² = 9 + 16 = 25

Par conséquent, l'hypoténuse est:

Hypoténuse = √25 = 5

- Exercice 1

Calculez les raisons trigonométriques des angles indiqués dans les triangles suivants:

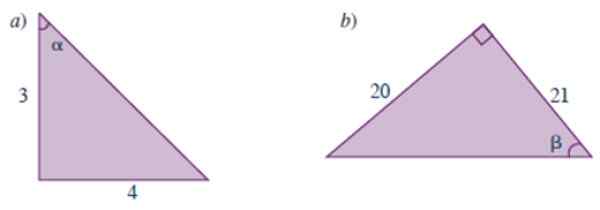figure 3.- Les triangles de l'année résolus 1. Source: Carena, M. 2019. Manuel des mathématiques de préunité.

Solution à

Ce triangle est le même sur la figure 3, mais ils nous demandent les raisons trigonométriques de l'autre angle aigu, indiqué α. La déclaration n'offre pas la valeur de l'hypotenusa, cependant, par application du théorème de Pythagore, nous savons qu'il vaut 5.

Les raisons peuvent être calculées directement à partir de la définition, en faisant attention lors de la sélection de la jambe qui est l'opposé de l'angle α pour calculer Sen α. Voyons:

• sin α = 4/5
• cos α = 3/5
• Tg α = 4/3
• cot α = ¾
• Sec α = 1 / (3/5) = 5/3
• dommage α = 1 / (4/5) = 5/4

Et comme nous pouvons le voir, les valeurs des raisons trigonométriques ont été échangées. En effet, α et θ sont des angles complémentaires, ce qui signifie qu'ils ajoutent 90º. Dans ce cas, il est accompli que Sen α = cos θ et ainsi de suite pour les autres raisons.

Solution B

Calcularons l'hypoténuse du triangle à travers le théorème de Pythagore:

Hypoténuse² = 20² + vingt-et-un² = 841

√841 = 29

Ensuite, les 6 raisons trigonométriques de l'angle β sont:

• Sen β = 20/29
• cos β = 21/29
• TG β = 20/21
• Cot β = 21/20
• Sec β = 1 / (21/29) = 29/21
• dommage β = 1 / (20/29) = 20/29

Peut vous servir: opérations combinées

- Exercice 2

a) Trouvez la valeur de x sur la figure.

b) Calculez le périmètre des 3 triangles indiqués.

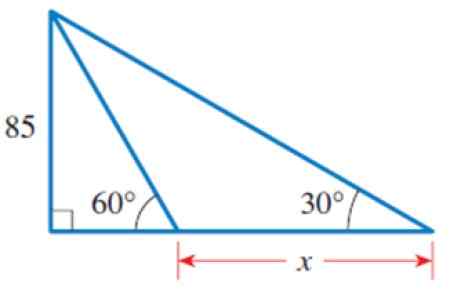Figure 4. Les triangles de l'année résolus 2. Source: Stewart, J. Précaulement: mathématiques pour le calcul.

Solution à

Dans la figure, nous pouvons identifier plusieurs triangles, en particulier le triangle rectangle de la gauche, qui a une catégorie égale à 85 et l'angle aigu 60º.

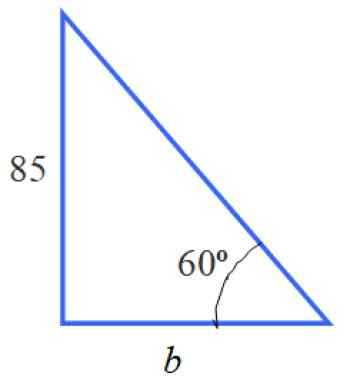Figure 5. Le triangle à gauche.

Avec les informations de ce triangle, nous pouvons calculer le côté B. Ce n'est pas la mesure que la déclaration demande, mais connaître sa valeur est une étape précédente.

Pour déterminer la raison appropriée est Tg 60 º = 85 / B, car B est la jambe adjacente à 60 ° et 85 est l'opposé de ce angle. Donc:

B = 85 / tg 60º = 85 / √3

Une fois connu B, nous utiliserons le triangle rectangle grand et extérieur, qui a un côté commun avec le triangle précédent: celui qui mesure 85. C'est le cateto opposé à l'angle de 30º.

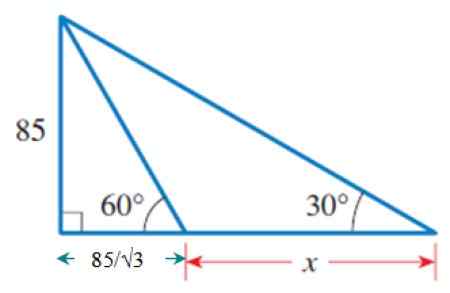Figure 6. Le triangle extérieur, dont une partie de la base est déjà connue.

De là:

Cateto adjacent à 30º = (85 / √3) + x

Maintenant, nous pouvons soulever ce qui suit:

85 / [(85 / √3) + x] = tg 30º

Ce qui est à carré-crochets multipliez le tg à 30 ° T:

85 = [(85 / √3) + x]. Tg 30º

Application de la propriété distributive de la multiplication:

85 = Tg 30º. (85 / √3) + x. Tg 30º

Donc:

X.Tg 30º = 85 - Tg 30º. (85 / √3) = 85 [1 - tg 30º . (1 / √3)] = 85 . (2/3) = 170/3

Remplacement de la valeur TG 30º = √3 / 3:

x = (170/3) ÷ (√3 / 3) = 98.quinze

Solution B

Périmètre du petit triangle

Être h₁ L'hypoténuse de ce triangle, qui peut être calculée par le théorème de Pythagore ou par une raison trigonométrique, par exemple COS 60º:

cos 60 º = 85 / √3 / h₁→ H₁ = (85 / √3) ÷ cos 60º = 98.1

Pour trouver P, le périmètre de ce triangle, nous ajoutons simplement les 3 côtés:

Peut vous servir: statistiques descriptives: historique, caractéristiques, exemples, concepts

P = 85 + (85 / √3) + 98.1 = 232.2

Périmètre du triangle externe

Être h₂ à l'hypoténuse du triangle externe:

Sen 30º = 85 ÷ h₂  

H₂ = 85 ÷ sin 30º = 170

Pour ce triangle, le périmètre est:

P = 85 + [(85 / √3) + 98.15] + 170 = 402.22

Périmètre du triangle non rectangulaire

De ce triangle, nous connaissons déjà tous ses côtés:

P = x + h₁ + H₂ = 98.15 + 98.15 + 170 = 366.3

Applications des raisons trigonométriques

Les raisons trigonométriques ont de nombreuses applications pratiques, par exemple les hauteurs peuvent être calculées.

Supposons qu'un château d'eau soit à 325 pieds d'un bâtiment. Un observateur situé dans une fenêtre note que l'angle d'élévation de l'extrémité supérieure de la tour est de 39 º, tandis que l'angle de dépression avec lequel la base de la tour est vue est de 25º. Merveilles:

a) Quelle est la hauteur de la tour?

b) Combien coûte la fenêtre?

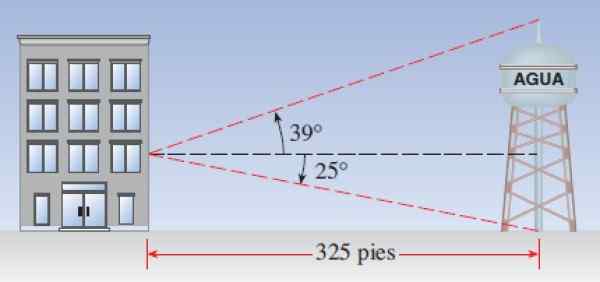Figure 7. Schéma de calcul de la hauteur du Vista Torre d'un bâtiment. Source: Stewart, J. Précaulement: mathématiques pour le calcul.

Solution à

Du cateto en face à 39 du triangle supérieur, nous obtenons une partie de la réponse:

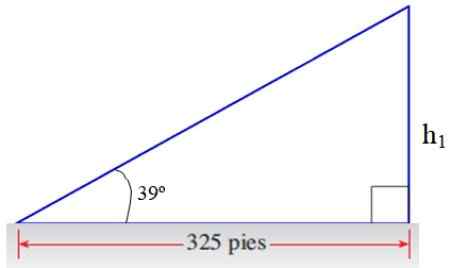Figure 8. Triangle pour l'exercice d'application. Source: F. Zapata.

H₁/ 325 = Tg 39º → H₁ = 325 . Tg 39º pieds = 263.Deux pieds

D'une manière similaire, nous obtenons le reste de la hauteur de la tour, appelée h₂ Du triangle inférieur:

H₂/ 325 = Tg 25º → H₂ = 325 . Tg 25º pieds = 151.6 pieds

La hauteur totale de la tour est h₁ + H₂ = 263.2 + 151.6 pieds = 414.7 pieds.

Solution B

La fenêtre est précisément à une hauteur h₂ du sol:

H₂ = 151.6 pieds.

Les références

1. Carena, m. 2019. Manuel des mathématiques de préunité. Université nationale de la côte.
2. Hoffman, J. Sélection de problèmes de mathématiques. Volume 3.
3. Jiménez, R. 2008. Algèbre. Prentice Hall.
4. Stewart, J. 2006. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
5. Zill, D. 1984. Algèbre et trigonométrie. McGraw Hill.