Qu'est-ce que la vitesse linéaire? (Avec des exercices résolus)

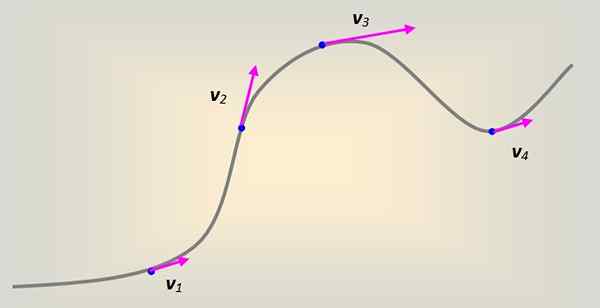
La Vitesse linéaire Il est défini comme celui qui est toujours tangentiel à la trajectoire suivie de la particule, peu importe. Si la particule se déplace toujours dans une trajectoire rectiligne, il n'y a aucun problème à imaginer comment le vecteur de vitesse accompagne cette ligne droite.

Cependant, en général, le mouvement est effectué sur une courbe arbitraire. Chaque partie de la courbe peut être modélisée comme si elle faisait partie d'un cercle radio pour, qui à chaque point est tangent au chemin suivi.

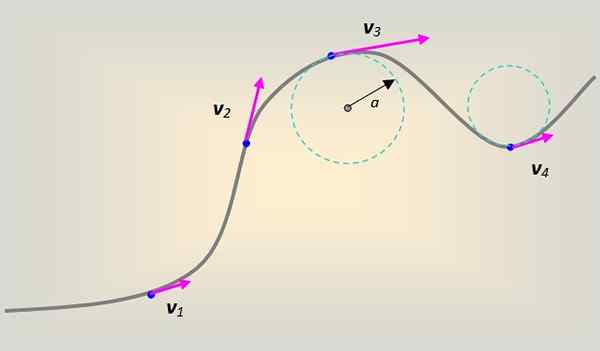Figure 1. Vitesse linéaire sur un mobile qui décrit une trajectoire curviligne. Source: auto-faite.

Dans ce cas, la vitesse linéaire s'accompagne de tangentiellement et à tout moment à la courbe à chaque point de celui-ci.

La vitesse linéaire instantanée mathématique est la dérivée de la position par rapport au temps. Être r le vecteur de position de la particule en un instant t, Ensuite, la vitesse linéaire est donnée par l'expression:

V = r'(T) = Dr / dt

Cela signifie que la vitesse linéaire ou la vitesse tangentielle, comme on l'appelle également, n'est rien d'autre que le changement de position par rapport au temps.

[TOC]

Vitesse linéaire dans le mouvement circulaire

Lorsque le mouvement est sur une circonférence, nous pouvons aller à côté de la particule à chaque point et voir ce qui se passe dans deux directions très spéciales: l'une d'entre elles est celle qui pointe toujours le centre. Ceci est l'adresse radial.

L'autre direction importante est celle qui se déroule sur la circonférence, c'est l'adresse tangentiel Et la vitesse linéaire l'a toujours.

Peut vous servir: pression manométrique: explication, formules, équations, exemples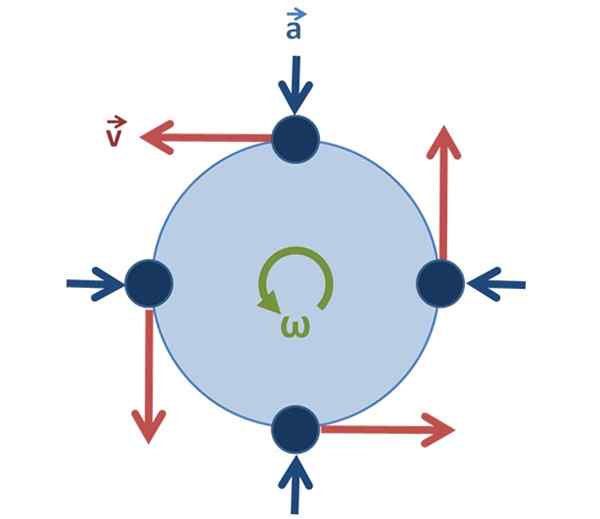Figure 2. Mouvement circulaire uniforme: le vecteur de vitesse change la direction et la direction lorsque la particule tourne, mais sa magnitude est la même. Source: Original par utilisateur: Brews_ohare, svged by utilisateur: sjlegg [cc by-sa 3.0 (https: // CreativeCommons.Org / licences / by-sa / 3.0)].

Dans le cas du mouvement circulaire uniforme, il est important oui il reste inchangé.

Pour ce mouvement, la position en fonction du temps est donnée par ST), où s c'est lui Arc tourné et t C'est le moment. Dans ce cas, la vitesse instantanée est donnée par l'expression V = ds / dt Et c'est constant.

Si l'ampleur de la vitesse varie également (nous savons déjà que la direction le fait toujours, sinon le mobile ne pourrait pas tourner), nous sommes confrontés à un mouvement circulaire varié, pendant lequel le mobile en plus de rotation, il peut s'arrêter ou accélérer.

Vitesse linéaire, vitesse angulaire et accélération centripète

Le mouvement des particules peut également être vu du point de vue du angle de balayage, Au lieu de le faire à partir du but parcouru. Dans ce cas, on parle de la vitesse angulaire. Pour un mouvement sur un cercle radio R, Il existe une relation entre l'arc (en radians) et l'angle:

S = r θ

Dérivant par rapport aux deux côtés:

ds / dt = r (dθ/ dt)

Appeler la dérivée de θ par rapport à t comme vitesse angulaire Et le dénotant avec la lettre grecque ω "Omega", vous avez cette relation:

v = ΩR

Accélération centripète

Chaque mouvement circulaire a accélération centripète, qui est toujours dirigé vers le centre de la circonférence. Elle prend soin que la vitesse change pour se déplacer avec la particule lorsqu'elle tourne.

Il peut vous servir: Courbe d'étalonnage: à quoi sert-il, comment le faire, des exemples

Accélération centripète pour_c soit pour_R Il pointe toujours vers le centre (voir figure 2) et est lié à la vitesse linéaire de cette manière:

pour_c = V² / R

Et avec la vitesse angulaire comme:

pour_c = (ΩR)² / R = Ω²R

Pour un mouvement circulaire uniforme, la position ST) C'est de la forme:

S (t) = SO + VT

De plus, le mouvement circulaire varié doit avoir une composante de l'accélération appelée Accélération tangentielle pour_T, Cela traite de la modification de l'ampleur de la vitesse linéaire. Ouais pour_T  C'est constant, La position est:

S (t) = s_soit + V_soitT + ½ A_Tt²

Avec V_soit Comme la vitesse initiale.

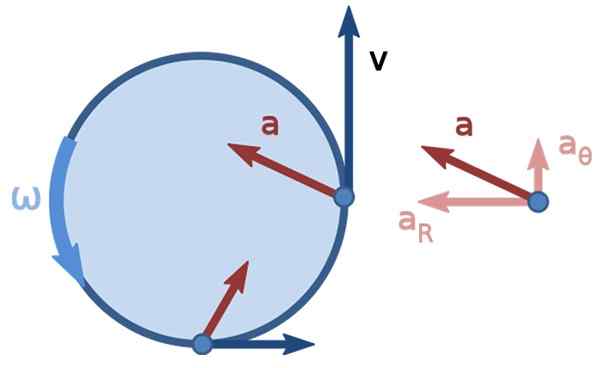figure 3. Mouvement circulaire non uniforme. Source: non uniforme_circular_motion.PNG: Brews Oharedorivative Work: Kooning Jons [CC By-Sa 3.0 (https: // CreativeCommons.Org / licences / by-sa / 3.0)].

Exercices de vitesse linéaire résolus

Les exercices résolus contribuent à clarifier la bonne utilisation des concepts et des équations données.

-Exercice résolu 1 

Un insecte se déplace sur un demi-cercle de rayon r = 2 m, à partir du repos au point un temps augmentant sa vitesse linéaire, à un taux de p m / s². Trouver: a) Après quelle heure il atteint le point B, b) le vecteur de vitesse linéaire à ce moment, c) l'accélération du vecteur à ce moment.

Figure 4. Un insecte part de A et atteint B sur une trajectoire semi-circulaire. Il a une vitesse linéaire. Source: auto-faite.

Solution

a) L'énoncé indique que l'accélération tangentielle est constante et vaut π m / s², Ensuite, il est valable d'utiliser l'équation pour un mouvement uniformément varié:

S (t) = s_soit + V_soitT + ½ A_T.t²

Avec s_soit = 0 et V_soit = 0:

S (t) = ½ a_T.t²

S = πR (La moitié de la longueur de circonférence)

T = (2. πR / /pour_T) ^½ S = (2π.2 / π)^½S = 2 S

b) v (t) = v_soit + pour_T. T = 2π SP

Au point B, le vecteur de vitesse linéaire pointe dans la direction verticale dans la direction (-et):

Peut vous servir: quelle est la constante diélectrique?

V (t) = 2π SP(-et)

c) L'accélération tangentielle est déjà faite, l'accélération centripète est manquante pour avoir le vecteur de vitesse pour:

pour_c = V² / R = (2π)² / 2 m / s² = 2π² SP²

pour = A_c (-X) + a_T (-et) = 2π²(-X) + π (-et) SP²

-Exercice résolu 2

Une particule tourne dans un cercle radio 2.90 m. Dans un moment particulier, son accélération vaut 1.05 m / s² dans une direction telle qui forme 32 avec sa direction de mouvement. Trouvez votre vitesse linéaire à: a) ce moment, b) 2 secondes plus tard, en supposant que l'accélération tangentielle est constante.

Solution

a) La direction du mouvement est précisément l'adresse tangentielle:

pour_T = 1.05 m / s² . cos 32º = 0.89 m / s² ; pour_C = 1.05 m / s² . Sen 32º = 0.56 m / s²

La vitesse efface de pour_c = V² / R comme:

v = (r.pour_c)^1/2  = 1.27 m / s

b) L'équation du mouvement uniformément varié est valide comme suit: V = V_soit + pour_TT = 1.27 + 0.89 .2² m / s = 4.83 m / s

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill. 84-88.
2. Figueroa, D. Série physique pour la science et l'ingénierie. Volume 3. Édition. Cinématique. 199-232.
3. Giancoli, D.  2006. Physique: principes avec applications. 6^e… Ed Prentice Hall. 62-64.
4. Mouvement relatif. Récupéré de: cours.Lumenarning.com
5. Wilson, J. 2011. Physique 10. Pearson Education. 166-168.