Qu'est-ce que l'impédance acoustique? Applications et exercices

La impédance acoustique o L'impédance acoustique spécifique est la résistance des moyens matériels pour le passage des ondes sonores. Il est constant pour un certain milieu, qui va d'une couche rocheuse à l'intérieur de la terre vers le tissu biologique.

Dénotant une impédance acoustique z, de manière mathématique, il doit:

Z = ρ.V

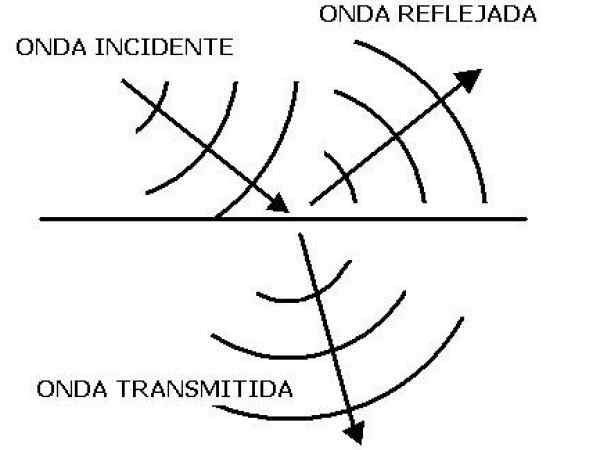
Figure 1. Lorsqu'une onde sonore affecte la bordure de deux moyens différents, une partie est reflétée et une autre est transmise. Source: Wikimedia Commons. Cristobal aeorum / cc by-sa (https: // CreativeCommons.Org / licences / by-sa / 4.0)

Où ρ est densité et v la vitesse du son du milieu. Cette expression est valable pour une onde plate en se déplaçant dans un fluide.

Dans les unités du système international, la densité est disponible en kg / m³ Et la vitesse en m / s. Par conséquent, les unités d'impédance acoustique sont kg / m².s.

De même, l'impédance acoustique est définie comme le quotient entre la pression P et la vitesse:

Z = p / v

Exprimé de cette manière, Z est analogue à la résistance électrique r = v / i, où la pression représente le papier de tension et de vitesse celui du courant. Autres unités Z s'ils seraient PA.s / m o n.VOUS³, complètement équivalent à ceux précédemment donnés.

[TOC]

Transmission et reflet de l'onde sonore

Lorsque vous avez deux moyens différents d'impédances z₁ et Z₂, Une partie d'une onde sonore qui affecte l'interface des deux peut être transmise et une autre partie peut être reflétée. Cette vague reflétée ou écho est celle qui contient des informations importantes sur le deuxième milieu.

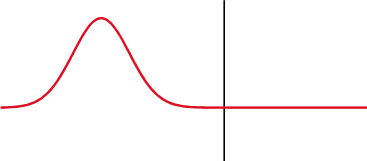Figure 2. Impulsion incident, impulsion transmise et impulsion réfléchie. Source: Wikimedia Commons.

La façon dont l'énergie transportée par l'onde est distribuée dépend des coefficients de réflexion R et T transmission, deux quantités très utiles pour étudier la propagation de l'onde sonore. Pour le coefficient de réflexion est le quotient:

R = i_r / Yo_soit

Où je_soit C'est l'intensité de l'onde incidente_r C'est l'intensité de l'onde réfléchie. De même, vous avez le coefficient de transmission:

T = i_t / Yo_soit

Maintenant, il peut être démontré que l'intensité d'une vague plate est proportionnelle à sa largeur:

Il peut vous servir: Duromètre: à quoi sert-il, comment fonctionne, les pièces, les types

I = (1/2) z.Ω² .POUR²

Où z est l'impédance acoustique du milieu et ω est la fréquence de l'onde. En revanche, le rapport entre l'amplitude transmise et l'amplitude incidente est:

POUR_t/POUR_soit = 2Z₁/ (Z₁ +Z₂)

Qui permet le quotient et_t / Yo_soit  Il s'exprime en termes d'amplitudes des ondes incidents et transmise comme:

Toi_t / Yo_soit = Z₂POUR_t² / Z₁POUR_soit²

À travers ces expressions, R et T sont obtenus en termes d'impédance acoustique z.

Coefficients de transmission et de réflexion

Le quotient antérieur est précisément le coefficient de transmission:

T = (z₂/ Z₁) [2.Z₁/ (Z₁ +Z₂)]² = 4Z₁Z₂ / (Z₁ +Z₂)²

Étant donné que les pertes ne sont pas envisagées, il est réalisé que l'intensité de l'incident soit la somme de l'intensité transmise et de l'intensité réfléchie:

Toi_soit = I_r + Toi_t → (je_r / Yo_soit) + (I_t / Yo_soit) = 1

Cela nous permet de trouver une expression pour le coefficient de réflexion en termes d'impédances des deux supports:

R + t = 1 → r = 1 - t

Effectuer une certaine algèbre pour réorganiser les termes, le coefficient de réflexion est:

R = 1 - 4Z₁Z₂ / (Z₁ +Z₂)² = (Z₁ - Z₂)²/ (Z₁ +Z₂)²

Et comme dans l'impulsion réfléchie est les informations liées au deuxième milieu, le coefficient de réflexion est d'un grand intérêt.

Ainsi, lorsque les deux médias ont une grande différence d'impédance, le numérateur de l'expression précédente devient plus élevé. Alors l'intensité de l'onde réfléchie est élevée et contient de bonnes informations sur le milieu.

Quant à la partie de la vague transmise à ce deuxième milieu, il est progressivement atténué et l'énergie est dissipée sous forme de chaleur.

Applications et exercices

Les phénomènes de transmission et de réflexion donnent naissance à diverses applications très importantes, par exemple le sonar développé pendant la Seconde Guerre mondiale et qui sert à détecter des objets. Soit dit en passant, certains mammifères tels que les chauves-souris et les dauphins ont un système de sonar construit.

Ces propriétés sont également largement utilisées pour étudier l'intérieur de la Terre dans les méthodes de prospection sismique, pour obtenir des images médicales par échographie, la mesure de la densité osseuse et la capture d'images de différentes structures à la recherche de défaillances et de défauts.

Peut vous servir: Modèle atomique Thomson: caractéristiques, postulats, particules subatomiques

L'impédance acoustique est également un paramètre important lors de l'évaluation de la réponse solide d'un instrument de musique.

- Exercice résolu 1

La technique d'échographie pour obtenir des images de tissus biologiques utilise des impulsions sonores à haute fréquence. Les échos contiennent des informations sur les organes et les tissus qui traversent, ce logiciel est responsable de la traduire dans une image.

Une impulsion à ultrasons est influencée à l'interface gras-musculus. Avec les données fournies, trouvez:

a) l'impédance acoustique de chaque tissu.

b) Le pourcentage d'échographie reflété dans l'interface entre la graisse et le muscle.

Graisse

• Densité: 952 kg / m³
• VITESSE SAISE: 1450 m / s

Muscle

• Densité: 1075 kg / m³
• Vieds sonore: 1590 m / s

Solution à

L'impédance acoustique de chaque tissu remplace dans la formule:

Z = ρ.V

De cette manière:

Z_graisse = 952 kg / m³ x 1450 m / s = 1.38 x 10⁶ kg / m².s

Z_muscle = 1075 kg / m³ x 1590 m / s = 1.71 x 10⁶  kg / m².s

Solution B

Pour trouver le pourcentage d'intensité reflété dans l'interface des deux tissus, le coefficient de réflexion donné par:

R = (z₁ - Z₂)²/ (Z₁ +Z₂)²

Ici z_graisse = Z₁ et Z_muscle = Z_2. Le coefficient de réflexion est un montant positif, qui est garanti par les carrés de l'équation.

Remplacement et évaluation:

R = (1.38 x 10⁶ - 1.71 x 10⁶ )²  / (1.38 x 10⁶ + 1.71 x 10⁶ )² = 0.0114.

En multipliant par 100, nous aurons le pourcentage réfléchi: 1.14% de l'intensité de l'incident.

- Exercice résolu 2

Une onde sonore a un niveau d'intensité 100 décibels et affecte normalement la surface de l'eau. Déterminez le niveau d'intensité de l'onde transmise et celle de l'onde réfléchie.

Peut vous servir: frottement visqueux (force): coefficient et exemples

Données:

Eau

• Densité: 1000 kg / m³
• VITESSE SAISE: 1430 m / s

Air

• Densité: 1.3 kg / m³
• VITESSE SON-SON: 330 m / s

Solution

Le niveau d'intensité des décibels d'une onde sonore est indiqué comme L, est sans dimension et est donné par la formule:

L = 10 log (i / 10^-12)

Raisage à 10 des deux côtés:

dix ^{L / 10} = I / 10^-12

Comme l = 100, se traduit:

I / 10^-12 = 10^dix

Les unités d'intensité sont données en termes de puissance par unité de surface. Dans le système international, ils sont watt / m². Par conséquent, l'intensité de l'onde incidente est:

Toi_soit = 10^dix . dix^-12 = 0.01 W / M².

Pour trouver l'intensité de l'onde transmise, le coefficient de transmission est calculé, puis multiplié par l'intensité incidente.

Les impédances respectives sont:

Z_eau = 1000 kg / m³ x 1430 m / s = 1.43 x 10⁶ kg / m².s

Z_air = 1.3 kg / m³ x 330 m / s = 429 kg / m².s

Remplacement et évaluation dans:

T = 4Z₁Z₂ / (Z₁ +Z₂)² = 4 × 1.43 x 10⁶ X 429 / (1.43 x 10⁶ + 429)² = 1.12 x 10^-3

Ainsi, l'intensité de l'onde transmise est:

Toi_t = 1.12 x 10^-3 x 0.01 W / M² = 1.12 x 10^-5 W / m²

Son niveau d'intensité décibels est calculé par:

L_t = 10 log (i_t /dix^-12) = 10 log (1.12 x 10^-5 / dix^-12) = 70.3 dB

Pour sa part, le coefficient de réflexion est:

R = 1 - t = 0.99888

Avec cela, l'intensité de l'onde réfléchie est:

Toi_r = 0.99888 x 0.01 W / M² = 9.99 x 10^-3 W / m²

Et son niveau d'intensité est:

L_t = 10 log (i_r /dix^-12) = 10 log (9.99 x 10^-3 / dix^-12) = 100 dB

Les références

1. Andriessen, M. 2003. Cours de physique HSC. Jacaranda.
2. Baranek, L. 1969. Acoustique. Deuxième édition. Éditorial hispanique américain.
3. Kinsler, L. 2000. Fondamentaux de l'acoustique. Wiley et fils.
4. Lowrie, W. 2007. Géophysique fondamentale. 2e. Édition. la presse de l'Universite de Cambridge.
5. Wikipédia. IMPÉDANCE ACOUSTIQUE. Récupéré de: dans.Wikipédia.org.