Quel est le module de coupe, de rigidité ou de cisaillement? (Exercices résolus)

Il Module de coupe Décrire la réponse d'un matériel à l'application d'un effort de cisaillement qui le déforme. Les autres dénominations d'utilisation fréquente pour le module de coupe sont le cisaillement, les cisaillements, l'élasticité transversale ou le module d'élasticité tangentiel.

Lorsque les efforts sont faibles, les déformations sont proportionnelles à eux, selon la loi de Hooke, la constante de coupe étant la constante de proportionnalité étant. Donc:

Couper le module = effort de coupe / déformation

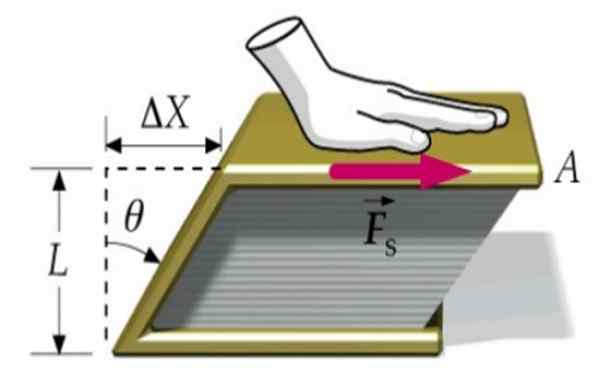
Figure 1. Un livre est déformé grâce à la force tangentielle FS. Source: F. Zapata.

Supposons qu'une force est appliquée sur le couvercle d'un livre, étant l'autre fixée à la surface de la table. De cette façon, le livre dans son ensemble ne bouge pas, mais se déforme lorsque le couvercle supérieur se déplace par rapport à celui inférieur dans la quantité Δx.

Le livre passe d'une section transversale rectangulaire à une section sous forme de parallélogramme, comme nous le voyons dans l'image supérieure.

Être:

τ = f / a

L'effort ou la tension de coupe, étant F l'ampleur de la force appliquée et POUR La zone sur laquelle il agit.

La déformation causée est donnée par le quotient:

Δ = Δx / L

Par conséquent, le module de coupe, que nous désignerons G, est:

De cette façon, le module de coupe est responsable de la mesure de la résistance des plans intérieurs de l'objet parallèle à l'effort appliqué.

Et comme Δx / l manque de dimensions, les unités de g sont les mêmes que celles de l'effort de coupe, qui est la raison entre la force et la zone.

Dans le système international d'unités, ces unités sont Newton / Square Metro ou Pascal, abrégé PA. Et dans les unités anglo-saxons, c'est une livre / pouce carré, abrégé psi.

[TOC]

Peut vous servir: mouvement rectiligne uniforme: caractéristiques, formules, exercices

Coupez le module pour divers matériaux

Sous l'action des forces de coupe comme celles décrites, les objets offrent une résistance similaire à celle du livre, dans laquelle les couches intérieures glissent. Ce type de déformation ne peut se produire que dans des corps solides, qui ont une rigidité suffisante pour s'opposer à la déformation.

D'un autre côté, les liquides n'offrent pas ce type de résistance, mais ils peuvent ressentir des déformations de volume.

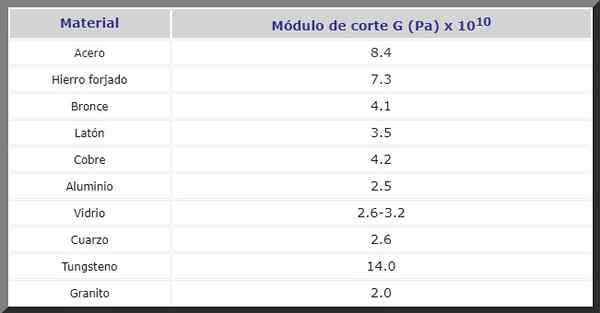
Figure 2. Les boulons dans les structures sont soumis à des efforts de coupe. Source: pixnio.

Ensuite, vous avez le module de coupe G en P pour divers matériaux fréquemment utilisés en construction et dans la fabrication de machines et de pièces de rechange de toutes sortes:

Mesure expérimentale du module de coupe

Pour trouver la valeur du module de coupe, vous devez tester des échantillons de chaque matériau et examiner votre réponse à l'application d'un effort de coupe.

L'échantillon est une tige faite avec le matériau, avec radio R et longueur L connu, qui est fixé à une extrémité, tandis que l'autre se connecte à l'axe d'une poulie libre.

La poulie a une corde attachée, à la fin duquel une pesée est suspendue qui exerce une force F Sur la tige à travers la corde. Et cette force produit à son tour un moment M Dans la tige, qui tourne ensuite un petit angle θ.

Un schéma d'assemblage peut être vu dans la figure suivante:

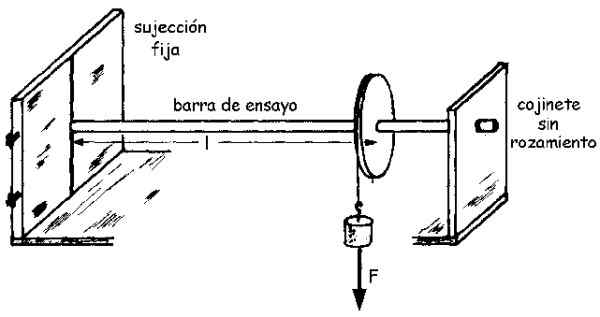figure 3.- Assemblage expérimental pour déterminer le module de cisaillement ou coupé d'une mince barre d'essai. Source: Université de Valladolid.

L'ampleur du moment M, que nous désignons comme M (sans gras) est lié à l'angle tourné θ à travers le module de coupe G selon l'équation suivante (il est déduit par une simple intégrale):

Comme l'ampleur du moment est égale au produit du module Force F par le rayon de la poulie R_p:

Il peut vous servir: Torricelli Expérience: mesures de pression atmosphérique, importance

M = f.R_p

Et la force est le poids qui pend W, ensuite:

M = w.R_p

Remplacement dans l'équation de l'ampleur du moment:

Vous avez la relation entre le poids et l'angle:

Comment trouver g?

Cette relation entre les variables W et θ Il est linéaire, donc les différents angles produits suspendues à différents poids sont mesurés.

Les couples de poids et d'angle sont des graphiques sur un papier millimètre, la meilleure ligne qui passe par les points expérimentaux est ajusté et la pente est calculée m de cette ligne.

 De là, il s'ensuit:

Exercices avec une solution

- Exercice 1

Une tige de 2.5 mètres de long et radio 4.5 mm est fixé à une extrémité. L'autre se connecte à une poulie radio de 75 cm qui a un poids 1 1.3 kg. L'angle tourné est 9.5e.

Avec ces données, il est demandé de calculer le module de coupe G de la tige.

Solution

De l'équation:

Gaz g:

Et les valeurs données dans l'énoncé sont remplacées, en prenant soin d'exprimer toutes les données du système international d'unités si:

R = 4.5 mm = 4.5 x 10 ^-3 m

R_p = 75 cm = 0.075

Pour passer des kilogrammes (ce sont en fait des kilogrammes - force) à Newton se multiplie par 9.8:

W = 1.3 kg-force = 1.3 x 9.8 n = 12.74 N

Et enfin, les diplômes doivent être sur Radians:

9.5e = 9.5 x2π / 360 radians = 0.1658 Radianes.

Avec tout cela, vous avez:

= 2.237 x 10^dix Pennsylvanie

- Exercice 2

Un cube de gel est de 30 cm côté. L'un de ses visages est fixé, mais en même temps, une force parallèle de 1 N est appliquée à la face opposée, ce qui, grâce à cela, se déplace de 1 cm (voir l'exemple du livre de la figure 1).

Il peut vous servir: aimantation: moment magnétique orbital et spin, exemples

Il est demandé de calculer avec ces données:

a) L'ampleur de la contrainte de cisaillement

b) Déformation unitaire δ

c) La valeur du module de coupe

Solution à

L'ampleur de la contrainte de cisaillement est:

τ = f / a

Avec:

A = côté² = (30 x 10^-2 cm)² = 0.09 m²

Donc:

τ = 1 n / 0.09 m² = 11.1 pa

Solution B

La déformation unitaire n'est autre que la valeur de Δ, donnée par:

Δ = Δx / L

Le déplacement du visage soumis à la force est de 1 cm, puis:

δ = 1/30 = 0.0333

Solution C

Le module de coupe et le quotient entre l'effort de coupe et la déformation unitaire:

G = effort de coupe / déformation

Donc:

G = 11.1 pa / 0.033 = 336.4 pa

Les références

1. Bière, f. 2010. Mécanique des matériaux. McGraw Hill. 5e. Édition.
2. Franco Garcia, à. Solide rigide. Entendre la mesure du module. Récupéré de: SC.Ehu.est.
3. Giancoli, D.  2006. Physique: principes avec applications. 6e. Ed Prentice Hall.
4. Resnick, r. (1999). Physique. Vol. 1. 3e édition. en espagnol. Société de rédaction continentale S.POUR. de c.V.
5. Université de Valladolid. Département de physique de la matière condensée. Sélection de problèmes. Récupéré de: www4.raisin.est.