Quel est le facteur de proportionnalité? (Exercices résolus)

Il facteur de proportionnalité o Constant de proportionnalité est un nombre qui indiquera combien le deuxième objet change par rapport au changement subi par le premier objet.

Par exemple, s'il est dit que la longueur d'un escalier est de 2 mètres et que l'ombre qui projette est de 1 mètre (le facteur de proportionnalité est 1/2), alors si l'escalier est réduit à une longueur de 1 mètre, le L'ombre réduira sa longueur proportionnellement, par conséquent, la longueur de l'ombre sera de 1/2 mètres.

Si au contraire, l'escalier est augmenté à 2.3 mètres alors la longueur de l'ombre sera 2.3 * 1/2 = 1.15 mètres.

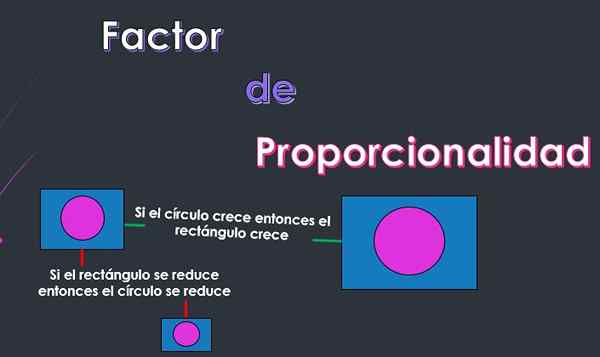
La proportionnalité est une relation constante qui peut être établie entre deux ou plusieurs objets de telle sorte que si l'un des objets souffre de changement, les autres objets subiront également un changement.

Par exemple, s'il est dit que deux objets sont proportionnels en termes de longueur, il aura si un objet augmente ou diminue sa longueur, alors l'autre objet augmentera ou diminuera également sa longueur proportionnellement.

Concept de facteur de proportionnalité

Le facteur de proportionnalité est, comme le montre l'exemple ci-dessus, une constante par laquelle il faut se multiplier pour obtenir l'autre ampleur.

Dans le cas précédent, le facteur de proportionnalité était de 1/2, car l'escalier «x» mesurait 2 mètres et l'ombre «Y» mesurait 1 mètre (moitié). Par conséquent, vous devez y = (1/2) * x.

Donc quand "x" change, alors "y" change également. Si c'est "y" celui qui change alors "x" changera également mais le facteur de proportionnalité est différent, dans ce cas, ce serait 2.

Exercices de proportionnalité

- Premier exercice

Juan veut préparer un gâteau à 6 personnes. La recette que Juan a dit que le gâteau a 250 grammes de farine, 100 grammes de beurre, 80 grammes de sucre, 4 œufs et 200 millilitres de lait.

Avant de commencer à préparer le gâteau, Juan s'est rendu compte que la recette qu'il a est pour un gâteau pour 4 personnes. Quelles devraient être les amplitudes que Juan doit utiliser?

Solution

Ici, la proportionnalité est la suivante:

4 personnes - 250 g de farine - 100 g de beurre - 80 g de sucre - 4 œufs - 200 ml de lait

6 personnes -?

Le facteur de proportionnalité dans ce cas est 6/4 = 3/2, qui pourrait être compris comme s'il était d'abord divisé par 4 pour obtenir les ingrédients par personne, puis se multiplier par 6 pour faire le gâteau pour 6 personnes.

En multipliant toutes les quantités par 3/2, les ingrédients sont pour 6 personnes sont:

6 personnes - 375 g de farine - 150 g de beurre - 120 g de sucre - 6 œufs - 300 ml de lait.

- Deuxième exercice

Deux véhicules sont identiques à l'exception de leurs pneus. Le rayon des pneus d'un véhicule est égal à 60 cm et le rayon des pneus du deuxième véhicule est égal à 90 cm.

Si après avoir fait une tournée, vous devez donner la quantité de tours que les pneus avec moins de rayon ont donné, c'était 300 tours. Combien de virages ont donné les plus grands pneus radio?

Solution

Dans cet exercice, la constante de proportionnalité est égale à 60/90 = 2/3. Donc, si les pneus radio mineurs ont donné 300 tours, alors les pneus avec la radio la plus élevée ont donné 2/3 * 300 = 200 tours.

- Troisième exercice

Il est connu que 3 travailleurs ont peint un mur de 15 heures à 15 heures en 5 heures. Combien peuvent-ils peindre 7 travailleurs en 8 heures?

Solution

Les données fournies dans cet exercice sont:

3 travailleurs - 5 heures - 15 m² de mur

Et ce qu'il se demande, c'est:

7 travailleurs - 8 heures -- ? Mur m².

Vous pourriez demander combien 3 travailleurs peindraient en 8 heures? Pour le savoir, la ligne de données fournie par le facteur de proportion 8/5 est multipliée. Cela montre en conséquence:

3 travailleurs - 8 heures - 15 * (8/5) = 24 m² de mur.

Maintenant, vous voulez savoir ce qui se passe si le nombre de travailleurs est augmenté à 7. Pour savoir quel effet cela produit la quantité de paroi peinte par le facteur 7/3. Cela donne la solution finale:

7 travailleurs - 8 heures - 24 * (7/3) = 56 m² de mur.

Les références

1. Cofré, un., & Tapia, L. (Année mille neuf cents quatre-vingts-quinze). Comment développer un raisonnement logique mathématique. Éditorial universitaire.
2. Physique de télérasports avancés. (2014). Edu nasz.
3. Giancoli, D. (2006). Volume physique I. Pearson Education.
4. Hernández, J. d. (s.F.). Cahier de mathématiques. Seuil.
5. Jiménez, J., Rofríguez, m., & Estrada, R. (2005). Mathématiques 1 sept. Seuil.
6. Neuhauser, C. (2004). Mathématiques pour la science. Pearson Education.
7. Peña, m. D., & Muntaner, à. R. (1989). Chimie physique. Pearson Education.
8. Segovia, b. R. (2012). Activités mathématiques et jeux avec Miguel et Lucía. BALDOMERO RUBIO SEGOVIA.
9. Tocci, r. J., & Widmer, n. S. (2003). Systèmes numériques: principes et applications. Pearson Education.