Caractéristiques de projection conique cartographique, avantages, inconvénients

La Projection conique cartographique Il se caractérise par la projection des points d'une surface sphérique à la surface d'un cône, dont le sommet est situé sur l'axe qui passe à travers les pôles et est tangent ou séchable vers la sphère. Le cône est une surface qui peut être ouverte dans un plan, formant un secteur angulaire et sans déformer les lignes projetées dessus.

Le mathématicien Johann Heinrich Lambert (1728 - 1777) a été celui qui a conçu cette projection, apparaissant pour la première fois dans son livre Perspective Freye (1759), où il a collecté plusieurs théories et réflexions sur les projections.  

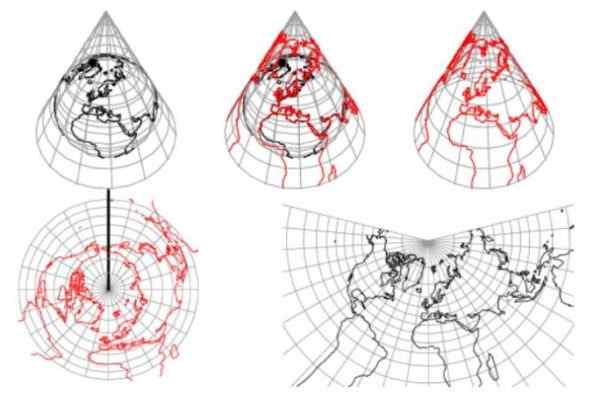
Figure 1. Projection conique. Source: Weisstein, Eric W. «Projection conique.”De Mathworld-A Wolfram Wew Resource.

Dans les projections coniques de la surface de la Terre, les méridiens deviennent des lignes radiales focalisées sur le sommet, avec le même espacement angulaire et les parallèles terrestres deviennent des arches circulaires concentriques au sommet.

La figure 1 montre que la projection conique ne permet pas de représenter les deux hémisphères. De plus, il est clairement observé que les distances sont déformées des parallèles qui interceptent le cône. 

Pour ces raisons, ce type de projection est utilisé pour représenter les régions de latitude moyennes, étendue de l'est en ouest et du nord-sud plus petit. Tel est le cas de la région continentale des États-Unis.

[TOC]

avantage

La Terre peut se rapprocher d'une sphère radio de 6378 km, considérant que toutes les masses terrestres et aquatiques sont sur cette grande sphère. Il s'agit de convertir cette surface, qui couvre un objet en trois dimensions, comme une sphère, dans un autre objet en deux dimensions: une carte plate. Cela apporte l'inconvénient que la surface incurvée est déformée, voulant la projeter dans l'avion.

Peut vous servir: la rivière Júcar

Les projections cartographiques, telles que la projection conique, essaient de résoudre ce problème avec la perte de précision possible plus faible. Il existe donc plusieurs options pour faire une projection, selon les caractéristiques qui sont mises en évidence.

Parmi ces caractéristiques importantes figurent les distances, la surface, les angles et plus. La meilleure façon de les garder toutes représentent le terrain en 3D à grande échelle. Mais ce n'est pas toujours pratique.

Le transport d'un globe partout n'est pas facile, car il occupe le volume. La surface entière de la terre ne peut pas non plus être vue en même temps, et il est impossible de reproduire tous les détails d'un modèle d'échelle.

Nous pouvons imaginer que la planète est une orange, éplucher l'orange et étaler la peau sur la table, essayant de reconstruire l'image de la surface de l'orange. Il est clair que beaucoup d'informations seront perdues dans le processus.

Les options de projection sont les suivantes:

- Projet sur un avion ou

- Sur un cylindre, qui peut être développé comme plan rectangulaire.

- Enfin à propos d'un cône.

Le système de projection conique a l'avantage précis sur les parallèles choisis pour intercepter le cône de projection.

De plus, il maintient une orientation pratiquement intacte à travers les méridiens, bien qu'il puisse déformer un peu l'échelle pour les latitudes éloignées des parallèles standard ou de référence. C'est pourquoi il est approprié de représenter des pays très étendus ou continents.

La projection conique équidistante

C'est le système de projection conique à l'origine utilisé par Ptolémée, un géographe grec qui vivait entre 100 et 170 ans. C. Par la suite en 1745, il a été amélioré.

Il peut vous servir: Cordillère de l'Ouest de Colombie

Il est fréquemment utilisé dans l'atlas des régions avec des latitudes intermédiaires. Il est adapté à montrer des zones à quelques degrés de latitude, et qui appartiennent à l'un des hémisphères équatoriaux.

Dans cette projection, les distances sont vraies dans les méridiens et dans les deux parallèles standard, c'est-à-dire les parallèles choisis pour intercepter avec le cône de projection. 

Dans la projection conique équidistante, un point sur la sphère s'étend radialement jusqu'à son intersection avec le cône tangent ou sécant, prenant comme centre de projection au centre de la sphère.

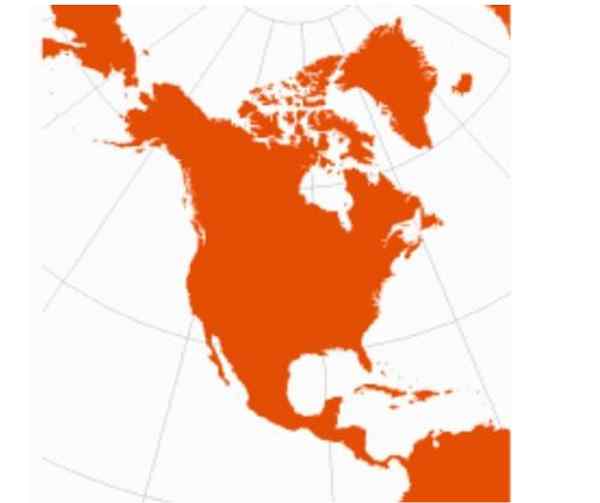Figure 2. Amérique du Nord avec une projection conique équidistante. Source: cartographie radicale.

Désavantages

Le principal inconvénient de la projection conique est qu'il n'est pas applicable aux régions équatoriales.

De plus, la projection conique n'est pas appropriée pour cartographier les grandes régions, mais plutôt des zones particulières, comme l'Amérique du Nord.

La projection conique d'Albert

Utilisez deux parallèles standard et préservez la zone, mais pas l'échelle et la forme. Ce type de projection conique a été présenté par H. C. Albers en 1805.

Toutes les zones de la carte sont proportionnelles à celles correspondantes sur Terre. Dans les régions limitées, les adresses sont relativement précises. Les distances correspondent à celles de la surface sphérique sur le parallèle standard.

Aux États-Unis, ce système de projection pour les cartes montrant les limites des états de l'Union est utilisé, pour lequel ils sont choisis comme parallèles standard sur 29,5 ° N et 45,5 ° N résultant comme une erreur maximale de l'échelle 1, 25%.

Les cartes faites avec cette projection ne conservent pas les angles correspondant à ceux de la sphère, ni ne conservent la perspective ou l'équidistance.

Peut vous servir: pétrologie

Projection conique selon Lambert

Il a été proposé en 1772 par le mathématicien et géographe suisse du même nom. Sa principale caractéristique est qu'il utilise un cône tangent ou sécant dans la sphère et que la projection conserve les angles invariants. Ces qualités le rendent très utile dans les lettres aéronautiques de navigation. 

Le United States Geological Service (USGS) utilise la projection conique de Lambert. Dans cette projection, les distances sont vraies tout au long des parallèles standard.

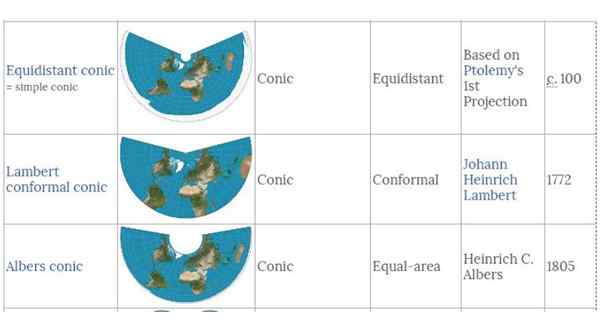figure 3. Différentes projections coniques de l'hémisphère nord, à droite, la date de création. Source: Wikimedia Commons.

Dans la projection conique de Lambert, les adresses restent raisonnablement précises. Les zones et les formes sont peu déformées dans des positions proches des parallèles standard, mais l'altération de la forme et de la zone augmente avec la séparation d'eux. 

Parce que l'objectif de cette projection est de maintenir des directions et des angles égaux aux originaux sur la sphère ou l'ellipsoïde, il n'y a pas de méthode géométrique pour l'obtenir, contrairement à la projection de Ptolémée équidistante.

Il s'agit plutôt d'une méthode de projection analytique, basée sur des formules mathématiques.

Les cartes de base USGS pour les 48 instructions continentales utilisent comme parallèles standard de 33 ° N et 45 ° N, en lançant une erreur maximale dans les cartes de 2,5%.

Pour les cartes de navigation en Alaska, les parallèles de base utilisés sont de 55 ° N et 65 ° N. D'un autre côté, l'Atlas national du Canada USA 49ºN et 77 ° N.

Les références

1. Geohunter. Le projet conique de Lambert conforme. Récupéré de: Geo.Chasseur.Cuny.Édu
2. Gisgographie. Projection conique: Lambert, Albers et Polyconic. Récupéré de: Gisgeographie.com
3. Gisgographie. Que sont les projections de cartes? Récupéré de: Gisgeographie.com
4. USGS. Projection de cartes. Récupéré de: icsm.Gouvernement.Au
5. Weisstein, Eric W. «Projet conique ALBERS Equal-Aea.”Récupéré de: Mathworld.Wolfram.com
6. Weisstein, Eric W. "Conic Projection" récupéré de: Mathworld.Wolfram.com
7. Weisstein, Eric W. "Lambert Conformal Conic Project" récupéré de: Mathworld.Wolfram.com
8. Wikipédia. Liste des projections de cartes. Récupéré de: dans.Wikipédia.com