Proportion

Une proportion est la relation de l'égalité qui existe entre deux raisons. Fait partie de l'ensemble. Volet

Qu'est-ce qu'une proportion?

Quand on parle de proportion Nous faisons référence à une pièce, un montant ou un composant considéré par rapport à l'ensemble de celui qui fait partie.

Par exemple, si nous voulons tailler une sculpture qui représente un corps humain de taille naturelle, toutes les parties doivent être en proportion, c'est-à-dire qu'elles ne doivent pas être plus petites ou plus grandes que ce qui correspond à la figure humaine.

Si nous voulons préparer une bonne paella, nous devons nous occuper de la proportion entre la quantité de riz et d'eau, les mollusques et les barrages de lapin, afin qu'il n'y ait pas d'excès ou de manque de l'une des trois quantités.

La proportion en mathématiques

En mathématiques, on parle de proportion ou de proportionnalité lorsque deux ou plusieurs nombres maintiennent une raison constante les uns avec les autres.

Regardons les fractions suivantes:

2/4 - 4/8 - 8/16

À première vue, nous pourrions avoir l'impression qu'ils représentent des nombres complètement différents, comme différents sont les trois numérateurs et les trois dénominateurs entre eux.

Mais si le numérateur est divisé entre le dénominateur, nous vérifierons que le résultat est le même dans les trois fractions: 0,5.

Si nous observons un peu plus, nous verrons que la deuxième fraction de la série a été obtenue en multipliant par 2 la première fraction; Et le troisième, à son tour, est le produit de la multiplication par deux la deuxième fraction:

2/4 x 2/2 = 4/8 -4/8 x 2/2 = 8/16

Ainsi, les trois fractions représentent le même quotient (0,5) et sont séparées par la même raison (2). C'est pourquoi nous pouvons dire qu'ils sont proportionnels.

Peut vous servir: Pentadecágono: éléments, classification, caractéristiques, exercice

La première et la troisième équation de la série sont également proportionnelles les unes aux autres, mais dans un rapport de 4:

2/4 x 4/4 = 8/16

Types de proportions

Les proportions peuvent être de plusieurs types, à savoir:

Proportion directe

Nous sommes confrontés à ce type lorsque, en augmentant l'une des quantités de la proportion, l'autre augmente également, et vice versa: si une quantité diminue, la même chose se produira avec l'autre.

Par exemple, réfléchissons à la distance dans laquelle une voiture parcourt en deux heures qui se déplace à 100 km / h. La réponse est de 200 kilomètres.

Augmentation maintenant de votre vitesse: elle ne passera plus à 100, mais 150 km / h. Combien de distance aura parcouru après deux heures? 300 kilomètres.

Ainsi, en augmentant la vitesse augmente également la distance parcourue dans une certaine période. Les deux éléments sont en proportion directe.

Proportion inverse

Dans ce cas, en augmentant le premier terme de la proportion, le second diminue et vice versa: si le second est augmenté, le premier terme diminue.

Revenons sur l'exemple de la voiture, mais cette fois, demandons-nous: combien de temps faut-il pour parcourir une distance de 100 kilomètres par voiture qui se déplace à 100 km / h? De toute évidence, une heure.

Maintenant, nous allons accélérer. Le véhicule atteint 200 km / h. Combien de temps faudra-t-il pour parcourir les mêmes 100 kilomètres? La réponse est de 0,5 ou 30 minutes.

Comme nous le voyons, en augmentant la vitesse, le temps dont le véhicule a besoin pour couvrir la distance est réduite. La vitesse et le temps sont donc en relation réversement proportionnelle.

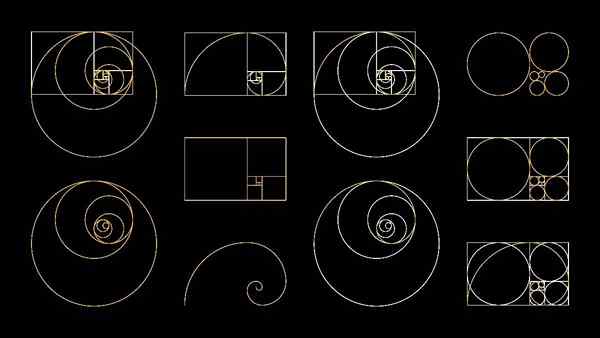
Proportion de l'auré

Également connu sous le nom de raison dorée, nombre d'or ou proportion divine, c'est un nombre irrationnel, c'est-à-dire qu'il ne peut pas être représenté par une fraction, car il a des décimales non périodiques infinies.

Peut vous servir: Multiples de 2: quelles sont et explications

Ce nombre, déjà découvert dans l'antiquité et symbolisé par la lettre grecque Fi (φ) en hommage au sculpteur Fidias (500-431 A.C.), représente une relation entre deux segments qui appartiennent à la même ligne.

Cette relation peut non seulement être vérifiée dans une abstraction géométrique sur papier, mais aussi dans les fleurs, les feuilles et un grand nombre de formes naturelles.

La proportion est très appréciée par les artistes en plastique, qui l'appliquent fréquemment dans leurs œuvres et le considèrent comme un critère de beauté avec une validité universelle.

Le numéro de proportion d'or est de 1 61803398874989.

Caractéristiques des proportions

Les proportions mathématiques se distinguent par trois caractéristiques, qui sont les suivantes:

1- Ils sont symétriques. Si une ampleur A est proportionnelle à une autre magnitude B, alors ce dernier B est également proportionnel à l'ampleur de. Entre eux, il y a une relation de symétrie ou de bidirection.

2- Ils sont transitifs. Dans une série proportionnelle qui comprend plus de deux amplitudes, il arrive que si l'amplitude A est proportionnelle au B, alors le B sera proportionnel à C et au second à D.

3- Ils ont une proportionnalité constante. Cette constante est la raison pour laquelle trois ou plusieurs amplitudes sont en proportion. Il est obtenu en conséquence en divisant l'anticedant entre la conséquence de l'une des amplitudes de la proportion.

Exemples de proportions

L'échelle des cartes

Vous aurez sûrement déjà remarqué que toutes les cartes ont, dans un coin ou en bas, quelques nombres séparés par deux points (:).

Selon la taille de la carte, ces chiffres varient entre 1:10.000, 1:50.000, 1: 100.000 ou même 1: 500.000.

Peut vous servir: chi carré (χ²): distribution, comment il est calculé, exemples

Ces nombres indiquent l'échelle de la carte et une échelle n'est rien d'autre qu'une proportion.

Par exemple, 1: 100.000 signifie que le territoire représenté par la carte est, en réalité, 100.000 fois plus grand que la carte que vous avez devant vous. Ou vice versa: la carte est de 100.000 fois plus petit que la zone représentée.

Feuilles d'impression

Lorsque nous faisons une impression sur l'ordinateur domestique, une boîte de dialogue apparaît dans laquelle nous pouvons configurer l'impression en fonction de nos besoins.

Là, nous pouvons sélectionner le type de feuille sur lequel nous allons imprimer, qui peut être A3, A4 ou A5.

Parce qu'il arrive que la relation entre les différents formats de feuilles soit proportionnelle.

Le plus grand de tous est A0, qui mesure un mètre carré. Il suit A1, qui est la moitié A0, c'est-à-dire qu'il est en proportion de ½.

Vient ensuite A3, qui correspond à ¼ A0 et ½ de A1.

A4 est égal à 1/8 de A0 et ¼ de A1. Et enfin A5, qui est 1/16 de A0 et 1/8 de A1.

Les références

1. (S / F). Constante de proportionnalité. Tiré de l'édu.Xunta.Fille.
2. (S / F). Proporter. Cuemath. Tiré de com.
3. (S / F). Proporter. Les mathématiques sont amusantes. Tiré de Mathsisfun.com.