Propriétés radicales

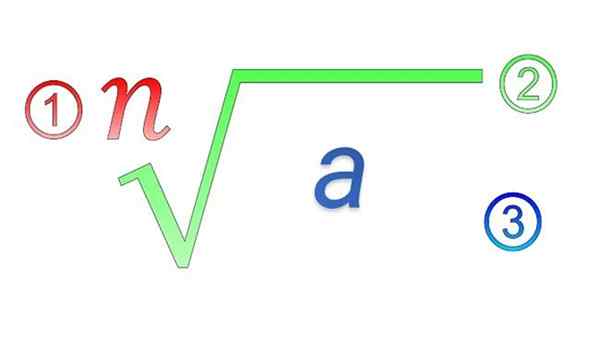
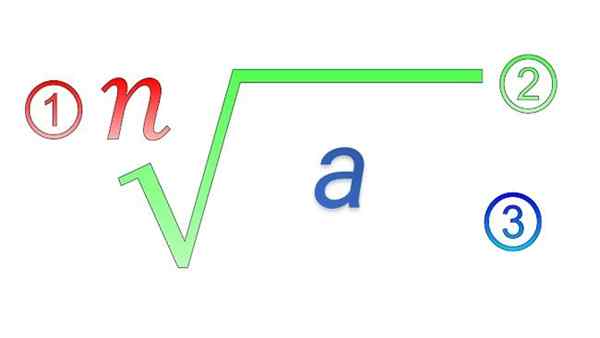Éléments radicaux: 1) Index; 2) symbole radical; 3) Quantité subratique

Quelles sont les propriétés des radicaux?

Le propriétés radicales Ce sont des opérations qui permettent de résoudre des problèmes complexes de radicaux et de pouvoirs. Le radical est le moyen de symboliser mathématiquement le n-eme d'un montant "a". Cette racine est une autre quantité, appelée "B", de sorte que son nom est précisément "A", il est donc valable d'écrire ce qui suit:

La valeur de "n" est un nombre naturel, qui est connu sous le nom d'indice racinaire, "A" est le Radical ou la quantité subratique, et "b" est le n-dém. "A" et "B" appartiennent à l'ensemble des nombres réels.

Si l'indice n'est pas écrit dans un radical, il est immédiatement compris que sa valeur est égale à 2 et lit «Root carrée de A».

Puisque "n" appartient à l'ensemble des nombres naturels, il peut s'agir d'un couple ou d'un numéro impair. Ensuite, les cas suivants se distinguent:

Pour "n" par

• Si A> 0 ou égal à 0, la racine n-alcale de «a» est positive ou 0, et est appelée racine principale.
• Quand < 0, no existe raíz n-ésima en el conjunto de los números reales, pero sí en los números complejos.

Pour «n» bizarre

• Oui A> 0, le n-dem de la racine «A» est positif.
• Quand< 0, la raíz n-ésima de “a” es negativa.

Quelques exemples sont les suivants:

Propriétés de tournage

Il est possible d'écrire le nom d'une quantité de montant comme puissance avec un exposant fractionnaire, c'est-à-dire un numéro rationnel.

Dans ce cas, l'indice de racine devient le dénominateur, tandis que l'exposant du montant subradique devient le numérateur:

Peut vous servir: fonction homographique: comment graphiquement, exercices résolus

Expression valide aussi longtemps que n ≠ 0, car aucune fraction avec un dénominateur n'est admise.

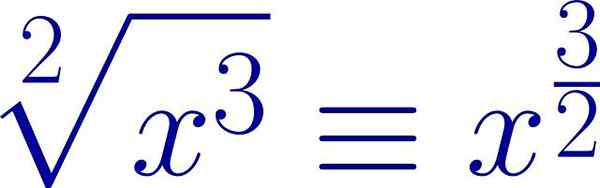Exemple d'une expression radicale écrite sous la forme d'un exposant fractionnaire. L'indice de racine est le dénominateur de l'exposant, tandis que la puissance de la diffusion est le numérateur. Source: Wikimedia Commons.

De cette façon, les mêmes propriétés qui s'appliquent aux pouvoirs peuvent être utilisées dans le cas des radicaux.

Pour les valeurs appartenant à l'ensemble des nombres réels, ces propriétés sont les suivantes:

1. Produit radical d'un indice égal

Dans le produit de deux (ou plus) radicaux du même index, les quantités subradicales sont multipliées, en maintenant l'index:

2. Quotient radical du même index

Le quotient entre la racine n-that de "a" et le n-eme de "b", étant b ≠ 0, est égal à la racine n-émotionnelle du quotient entre "a" et "b":

3. Racine

Pour trouver la racine n-émotionnelle du m -me du montant "A", le montant subratique est écrit sous une racine dont l'indice est le produit entre "N" et "M":

La procédure est facilement étendue aux racines imbriquées successives. L'indice de racine résultant est le produit de tous les indices, comme ceci:

4. Puissance radiculaire

Un N-That, élevé au pouvoir M, exprime le montant subratique de ladite puissance:

Cas particuliers:

1) Oui n = m, Le signe racine disparaît, laissant la base élevée à la puissance 1:

Qui est valable pour ≥ 0. En général, si l'index racine est un nombre pair, vous avez:

(Voir des exemples plus tard)

2) Oui m> n, La fraction M / N est incorrecte et la racine peut être simplifiée, par exemple, à la recherche de la fraction équivalente à M / N telle que le numérateur et le dénominateur sont des cousins ​​les uns avec les autres, ou réécrivant la quantité subradique et appliquant une partie des Propriétés décrites ici.

Peut vous servir: prismes et pyramides

(Voir des exemples plus tard)

5. Amplification radicale

Un radical peut être amplifié par un facteur q, Si l'indice de racine, ainsi que la puissance de la quantité subradique, se multiplient par ledit facteur, et cette opération n'implique pas la modification du résultat. Donc:

À condition qu'un ≥ 0 quand il est uniforme.

6. Introduction d'un facteur dans un radical

Si un facteur «B» positif multiplie un radical, il peut y passer, s'il atteint le même indice de racine. Dans ce cas:

7. Somme et soustraction des radicaux

Les radicaux peuvent ajouter et soustraire, tant qu'ils sont le même indice et ont le même montant subratique.

Lorsque deux ou plusieurs radicaux sont d'un indice égal et d'une quantité subratique, il est dit qu'ils sont Radicaux similaires.

Par exemple, les radicaux suivants sont similaires:

Au lieu de cela, ces radicaux ne sont pas similaires, car ils n'ont pas la même quantité subratique:

Ces deux ne sont pas non plus similaires:

Puisque l'indice radical n'est pas le même.

Des radicaux similaires peuvent être réduits à un, ajoutant ou soustrayant les coefficients qui les accompagnent.

Exemples de propriétés radicales

Exemple 1

Quelle est la valeur des racines suivantes?

La racine carrée de 32 peut être trouvée directement à l'aide de la calculatrice. Sa valeur est:

Les points suspendus indiquent qu'il y a une décimale infinie.

Si vous préférez ne pas travailler avec des nombres décimaux, la racine carrée de 32 peut également être calculée en décomposant 32 dans ses facteurs premiers:

32 = 2⁵

De cette façon, lors du remplacement, il est obtenu:

Peut vous servir: Diviseurs de 8: Quelles sont les explications faciles

Écrit comme un exposant fractionnaire:

La fraction 5/2 est incorrecte, donc le radical peut être simplifié, en utilisant les propriétés des pouvoirs:

Applique maintenant la propriété 1 ci-dessus:

Donc:

Pour sa part:

Depuis (−2)³ = −8.

Selon la propriété 4:

Et enfin, la racine carrée de -8 n'existe pas dans l'ensemble des nombres réels, bien que dans les nombres complexes.

Exemple 2

Compte tenu de l'opération suivante:

Est-il possible de réduire le résultat?

À condition que les radicaux soient similaires, il est possible de les réduire, mais pour cela, ils doivent avoir le même indice et la même quantité subratique. Dans l'exemple précédent, il a été vu que:

Une procédure analogue peut être utilisée pour écrire le premier ajout, de sorte que la quantité subradicale est égale à 2:

Ce radical est similaire à la précédente. Quant à la racine carrée de 81, c'est donc 9:

Exemple 3

Quelles propriétés sont nécessaires pour appliquer pour effectuer cette opération?

Nous devons appliquer les propriétés 3 et 5, qui sont respectivement la racine d'une racine et l'introduction d'une valeur radicale. Premièrement, la propriété 5 s'applique, pour introduire le «X» qui est en dehors de la racine la plus intérieure:

Et maintenant, l'expression est prête à appliquer la propriété 3, et à multiplier les indices respectifs de chaque radical:

Les références

1. Gonzales, D. 2011. Algèbre de base: théorie et pratique. 2e. Édition.
2. Haeussler, e. 2012. Précalation. 1er. Édition. Pearson.
3. Khan acadaem. Exposants et radicaux. Récupéré de: Khanacademy.org.
4. Larson, R. 2012. Précalation. 8e. Édition. Cengage Learning.
5. Stewart, J. 2007. Mathématiques pour le calcul. 5e. Édition. Cengage Learning.