Probabilité théorique comment le sortir, exemples, exercices

La Probabilité théorique (ou de Laplace) qu'un événement se produit qui appartient à un espace d'échantillon s, dans lequel tous les événements ont la même probabilité d'occurrence, il est défini en notation mathématique telle que: P (e) = n (e) / n ( S)

Où p (e) est la probabilité, donnée comme rapport entre le nombre total de résultats possibles de l'événement E, que nous appelons n (e), divisé par le nombre total n (s) des résultats possibles dans l'espace d'échantillonnage s.

Figure 1. Lors du lancement d'un dés à six côtés, la probabilité théorique que le visage avec trois points soit en haut est ⅙. Source: Pixabay.

La probabilité théorique est un nombre réel entre 0 et 1, mais il s'exprime souvent sous la forme d'un pourcentage, auquel cas la probabilité sera une valeur comprise entre 0% et 100%.

Le calcul de la probabilité d'occurrence d'un événement est très important dans de nombreux domaines, tels que l'activité boursier, les compagnies d'assurance, le jeu et bien d'autres.

[TOC]

Comment obtenir la probabilité théorique?

Un cas illustratif est le cas des rifas ou des loteries. Supposons que 1.000 billets pour Rifar un smartphone. Comme la tombola est effectuée au hasard, l'un des billets a la même chance d'être gagnant. 

Pour trouver la probabilité qu'une personne qui achète un billet avec le numéro 81 soit gagnant, le calcul suivant de Probabilité théorique:

P (1) = 1/1.000 = 0,001 = 0,1%

Le résultat précédent est interprété comme suit: Si la tombola est répétée infiniment, toutes les 1.000 fois le billet 81 serait sélectionné, en moyenne, une fois.

Si pour une raison quelconque, quelqu'un acquiert tous les billets est certain qu'il gagnera le prix. La probabilité de gagner le prix si vous avez tous les billets calculés comme suit:

Il peut vous servir: périmètre du cercle: comment le retirer et formules, exercices résolus

P (1.000) = 1.000/1.000 = 1 = 100%.

C'est-à-dire quelle probabilité 1 ou 100% signifie qu'il est totalement sûr que ce résultat se produira.

Si quelqu'un possède 500 billets, les possibilités de gagner ou de perdre sont les mêmes. La probabilité théorique de remporter le prix dans ce cas est calculée comme suit:

P (500) = 500/1.000 = ½ = 0,5 = 50%.

Celui qui n'achète aucun billet n'a aucune chance de gagner et sa probabilité théorique est déterminée comme ceci:

 P (0) = 0/1.000 = 0 = 0%

Exemples

Exemple 1

Vous avez une monnaie avec visage d'un côté et bouclier ou sceller dans l'autre. Lorsque la monnaie est lancée, quelle est la probabilité théorique d'être coûteux?

P (visage) = n (visage) / N ( visage + bouclier ) = ½ = 0,5 = 50%

Le résultat est interprété comme suit: Si un grand nombre de versions étaient effectuées, en moyenne tous les 2 emplacements, l'un d'eux est confronté.

En pourcentage, l'interprétation du résultat est que la fabrication d'un nombre infiniment grand de lancements, en moyenne tous les 100 d'entre eux, entraînerait un coût cher.

Exemple 2

Dans une boîte, il y a 3 billes bleues, 2 billes rouges et 1 vert. Quelle est la probabilité théorique que lorsque vous obtenez un marbre de la boîte, c'est du rouge?

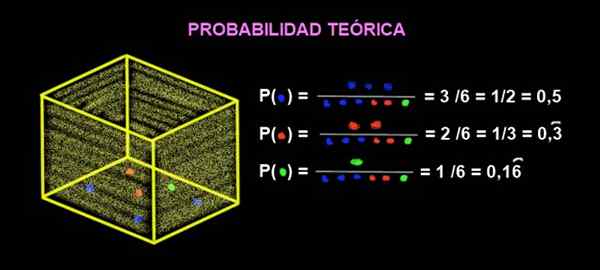Figure 2. Probabilité d'extraction des billes de couleur. Source: F. Zapata.

La probabilité qui vient rouge est:

P (rouge) = nombre de cas favorables / nombre de cas possibles

C'est-à-dire:

P (rouge) = nombre de billes rouges / nombre total de billes

Enfin, la probabilité qu'un marbre rouge soit:

P (rouge) = 2/6 = ⅓ = 0,3333 = 33,33%

Alors que la probabilité qu'en extrait un marbre vert est:

P (vert) = ⅙ = 0,1666 = 16,66%

Enfin, la probabilité théorique d'obtenir dans une extraction aveugle un marbre bleu est: 

P (bleu) = 3/6 = ½ = 0,5 = 50%

Il peut vous servir: propriétés radicales

Autrement dit, sur les 2 tentatives, le résultat sera bleu dans l'un d'eux et une autre couleur dans une autre tentative, sous la prémisse que le marbre extrait est reconstitué et que le nombre d'essais est très, très grand.

Exercices

Exercice 1

Déterminez la probabilité que lors du lancement d'un dés, une valeur est obtenue inférieure ou égale à 4.

Solution

Pour calculer la probabilité que cet événement se produise, la définition de la probabilité théorique s'appliquera:

P (≤4) = nombre de cas favorables / nombre de cas possibles

P (≤5) = 5/6 = = 83,33%

Exercice 2

Trouver la probabilité que dans deux hauteurs consécutives d'un dés à six faces normale, 2 fois 2 fois.

Solution

Pour répondre à cet exercice, il est pratique de faire une image pour montrer toutes les possibilités. Le premier chiffre indique le résultat du premier dés et le second le résultat de l'autre.

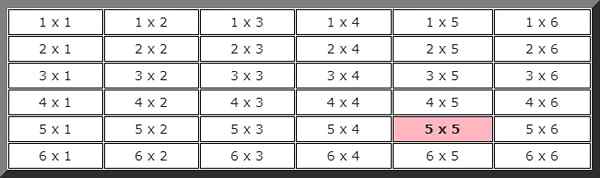
Pour calculer la probabilité théorique, nous devons connaître le nombre total de cas possibles, dans ce cas, comme on peut le voir dans le tableau précédent, il y a 36 possibilités.

Observant également la peinture, il s'ensuit que le nombre de cas favorable à l'événement qui, dans les deux versions consécutives, vient 5 n'est que 1, mise en évidence avec la couleur, donc la probabilité que cet événement se produise est:

P (5 x 5) = 1/33.

Ce résultat aurait également pu être atteint en utilisant l'une des propriétés de la probabilité théorique, qui indique que la probabilité combinée de deux événements indépendants est le produit de leurs probabilités individuelles.

Dans ce cas, la probabilité que dans la première version 5 soit ⅙. Le deuxième lancement est complètement indépendant du premier, donc la probabilité que 5 dans le second soit également ⅙. La probabilité combinée est donc:

Peut vous servir: Dérivés partiels: propriétés, calcul, exercices

P (5 × 5) = p (5) p (5) = (1/6) (1/6) = 1/36.

Exercice 3

Trouvez la probabilité qu'un nombre moins de 2 sort dans le premier lancement et dans le second un nombre de plus de 2 sort. 

Solution

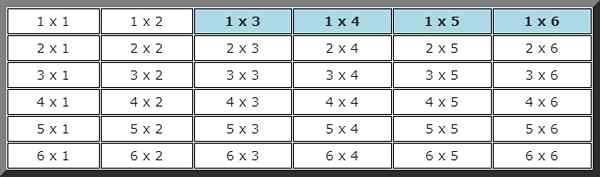
Encore une fois, vous devez construire un tableau d'événements possible, où ceux dans lesquels le premier lancement était inférieur à 2 et dans le second plus que 2 sont soulignés.

Au total, il y a 4 possibilités d'un total de 36. En d'autres termes, la probabilité de cet événement est:

P (2) = 4/36 = 1/9 = 0,1111 = 11,11%

Utilisation du théorème des probabilités qui indique:

La probabilité d'occurrence de deux événements indépendants est égal au produit de probabilités individuelles.

Il est obtenu un résultat identique:

P (2) = (1/6) (4/6) = 4/36 = 0,1111 = 11,11%

La valeur obtenue avec cette procédure coïncide avec le résultat précédent, par la définition théorique ou classique de la probabilité.

Exercice 4

Quelle est la probabilité qu'en lançant deux étant donné la somme des valeurs est 7.

Solution

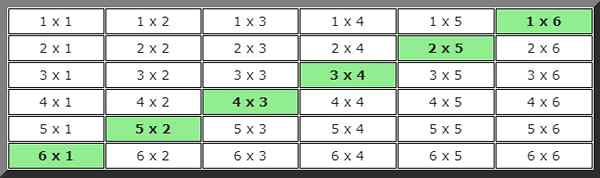
Pour trouver la solution dans ce cas, une image des possibilités a été développée dans laquelle les cas qui répondent à l'état des valeurs sont 7 ont été indiqués en couleur.

En regardant le tableau, 6 cas possibles peuvent être comptés, donc la probabilité est:

P (R&D II: 7) = 6/36 = 1/6 = 0,1666 = 16,66%

Les références

1. Canavos, g. 1988. Probabilité et statistiques: applications et méthodes. McGraw Hill.
2. Devore, J. 2012. Probabilité et statistiques pour l'ingénierie et la science. 8e. Édition. Cengage.
3. Lipschutz, s. 1991. Série Schaum: probabilité. McGraw Hill.
4. Obregón, je. 1989.Théorie de la probabilité. Limusa éditorial.
5. Walpole, R. 2007. Probabilité et statistiques pour l'ingénierie et la science. Pearson.