Formule de probabilité conditionnelle et équations, propriétés, exemples

La probabilite conditionnelle C'est la possibilité de survenue d'un certain événement, car un autre se produit comme condition. Ces informations supplémentaires peuvent modifier (ou peut-être pas) la perception que quelque chose se passera.

Par exemple, nous pouvons nous demander: «Quelle est la probabilité qu'il pleut aujourd'hui, car il y a deux jours, il ne pleut pas?". L'événement dont nous voulons connaître la probabilité est qu'il pleut aujourd'hui, et les informations supplémentaires qui conditionneraient la réponse est que "il y a deux jours, il ne pleut pas".

Figure 1. La probabilité qu'il pleut aujourd'hui car il a plu hier est également un exemple de probabilité conditionnelle. Source: Pixabay.

Être un Espace probabiliste composé de ω (espace d'échantillon), ℬ (événements aléatoires) et p (la probabilité de chaque événement), plus les événements a et b appartenant à ℬ.

La probabilité conditionnée qui se produit, puisque B, qui est désignée P (a│b), est définie de cette manière:

P (a│b) = p (a∩b) / p (b) = p (a et b) / p (b)

Où: p (a) est la probabilité d'occurrence de a, p (b) est la probabilité de l'événement b et est différent de 0, et p (a∩b) est la probabilité d'intersection entre a et b, c'est-à-dire ,, la probabilité que les deux événements se produisent (probabilité conjointe).

Ceci est une expression pour le théorème de Bayes appliqué à deux événements, proposé en 1763 par le théologien et mathématicien anglais Thomas Bayes.

[TOC]

Propriétés

-Toute probabilité conditionnelle se situe entre 0 et 1:

0 ≤ p (a│b) ≤ 1

-La probabilité que l'événement se produise, puisque cet événement se produit, est évidemment 1:

P (a│a) = p (a∩a) / p (a) = p (a) / p (a) = 1

-Si deux événements sont exclusifs, c'est-à-dire des événements qui ne peuvent pas se produire simultanément, alors la probabilité conditionnelle que l'un d'eux se produit est 0, car l'intersection est nulle:

P (a│b) = p (a∩b) / p (b) = 0 / p (b) = 0

-Si B est un sous-ensemble de A, alors la probabilité conditionnelle est également 1:

Peut vous servir: Toroid ou Toro Dona

P (b│a) = p (a∩b) / p (a) = 1

Important

P (a│b) Il n'est généralement pas égal à P (b│a), vous devez donc prendre soin de ne pas échanger des événements lors de la recherche de probabilité conditionnelle.

Règle générale de la multiplication

Plusieurs fois, vous souhaitez trouver la probabilité articulaire P (a∩b), au lieu d'une probabilité conditionnelle. Donc, grâce au théorème suivant, vous avez:

P (a∩b) = p (a et b) = p (a│b). P (b)

Le théorème peut être prolongé pour trois événements A, B et C:

P (a∩b∩c) = p (a et b et c) = p (a) · p (b│a) · p (c│a∩b)

Et aussi pour plusieurs événements, comme₁, POUR₂, POUR₃ Et plus, il peut être exprimé comme suit:

P (A₁∩ A₂ ∩ A₃… ∩ A_n) = P (a₁) . P (A₂│a₁). P (A₃│a₁∩ A₂) ... p (a_n│a₁∩ A₂∩… un_N-1)

Lorsque c'est le cas des événements qui se produisent en séquence et à différentes étapes, il est pratique d'organiser les données dans un diagramme ou un tableau. Cela facilite la visualisation des options pour atteindre la probabilité demandée.

Les exemples de cela sont le diagramme d'arbres et la tableau de contingence. De l'un d'eux, vous pouvez construire l'autre.

Exemples de probabilité conditionnelle

Examinons certaines situations dans lesquelles les probabilités d'un événement sont modifiées par la survenue d'une autre:

- Exemple 1

Dans un magasin sucré, deux types de gâteaux sont vendus: la fraise et le chocolat. Lors de l'enregistrement des préférences de 50 clients des deux sexes, les valeurs suivantes ont été déterminées:

-27 femmes, dont 11 préfèrent la fraise et 16 gâteau au chocolat.

-23 hommes: 15 chocolat et 8 fraises.

La probabilité qu'un client choisit un gâteau au chocolat puisse être déterminé en appliquant la règle de Laplace, selon laquelle la probabilité de tout événement est:

P = nombre d'événements favorables / nombre total d'événements

Dans ce cas, sur 50 clients, un total de 31 préfèrent le chocolat, de sorte que la probabilité soit p = 31/50 = 0.62. C'est-à-dire que 62% des clients préfèrent le gâteau au chocolat.

Peut vous servir: équations polynomiales

Mais serait-ce différent si le client est une femme? Ceci est un cas de probabilité conditionnelle.

Tableau de contingence

Grâce à une table d'urgence comme celle-ci, les totaux sont facilement visualisés:

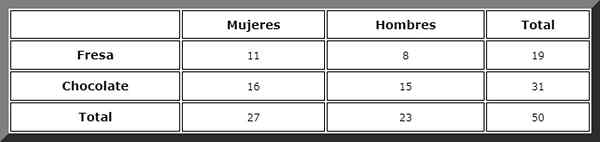
Ensuite, les cas favorables sont observés et la règle de Laplace est appliquée, mais avant de définir les événements:

-B est l'événement «client féminin».

-A est l'événement "préférez le gâteau au chocolat" étant une femme.

Nous allons à la colonne intitulée "femmes" et là, nous voyons que le total est de 27.

Ensuite, le cas favorable est recherché dans la ligne "chocolat". Il y a 16 événements de ceux-ci, donc la probabilité recherchée est directement:

P (a│b) = 16/27 = 0.5924

A 59.24% des femmes préfèrent le gâteau au chocolat.

Cette valeur coïncide lorsque nous contrasons avec la définition initialement donnée de la probabilité conditionnelle:

P (a│b) = p (a∩b) / p (b)

Nous nous assurons à travers la règle de Laplace et les valeurs du tableau:

P (b) = 27/50

P (A et B) = 16/50

Où p (a et b) est la probabilité que le client préfère le chocolat et est une femme. Maintenant, les valeurs sont remplacées:

P (a│b) = p (a et b) / p (b) = (16/50) / (27/50) = 16/27 = 0.5924.

Et il est prouvé que le résultat est le même.

- Exemple 2

Dans cet exemple, la règle de multiplication s'applique. Supposons que dans l'exposition d'un magasin, il y a un pantalon en trois tailles: petit, moyen et grand.

Dans beaucoup avec un total de 24 pantalons, dont il y a 8 de chaque taille et tous sont mélangés. Quelle serait la probabilité d'extraire deux d'entre elles et que les deux étaient petites?

Il est clair que la probabilité d'extraction de petits pantalons dans la première tentative est 8/24 = 1/3. Maintenant, la deuxième extraction est conditionnée au premier événement, car lorsque vous retirez un pantalon, il n'y en a plus 24, mais 23. Et si un petit pantalon est retiré, il y en a 7 au lieu de 8.

Peut vous servir: Principe multiplicatif: techniques de comptage et exemples

L'événement A consiste à éliminer un petit pantalon, en ayant pris un autre dans la première tentative. Et l'événement B est celui du petit pantalon au premier. Donc:

P (b) = 1/3; P (a│b) = 7/24

Enfin, grâce à la règle de multiplication:

P (a∩b) = (7/24).(1/3) = 7/72 = 0.097

Exercice résolu

Dans une étude de la ponctualité sur les vols aériens commerciaux, les données suivantes sont disponibles:

-P (b) = 0.83, est la probabilité qu'un avion prenne pour prendre un temps opportun.

-P (a) = 0.81, est la probabilité d'atterrir à temps.

-P (b∩a) = 0.78 C'est la probabilité que le vol arrive à temps en prenant un temps opportun.

Il est demandé de calculer:

a) Quelle est la probabilité que l'avion atterrit rapidement car il a décollé à temps?

b) La probabilité ci-dessus est la même que la probabilité qu'il soit sorti à temps si vous avez réussi à atterrir rapidement?

c) Et enfin: quelle est la probabilité qu'elle vienne à l'heure car elle n'est pas sortie à l'heure?

Figure 2. La ponctualité sur les vols commerciaux est importante, car les retards génèrent des pertes millionnaires. Source: Pixabay.

Solution à

Pour répondre à la question, la définition de la probabilité conditionnelle est utilisée:

P (a│b) = p (a∩b) / p (b) = p (a et b) / p (b) = 0.78/0.83 = 0.9398

Solution B

Dans ce cas, les événements sont échangés dans la définition:

P (b│a) = p (a∩b) / p (a) = p (a et b) / p (a) = 0.78/0.81 = 0.9630

Notez que cette probabilité est légèrement différente de la précédente, comme nous l'avons indiqué précédemment.

Solution C

La probabilité de ne pas être ponctuelle est 1 - p (b) = 1 - 0,83 = 0.17, nous l'appellerons p (b^C), Car c'est l'événement complémentaire pour prendre un temps opportun. La probabilité conditionnelle demandée est:

P (a│b^C) = P (a∩b^C) / P (b^C) = P (a et b^C) / P (b^C)

D'un autre côté:

P (a∩b^C) = P (atterrissage en temps) - P (atterrissage en temps et décollage de coups de pied) = 0.81-0.78 = 0.03

Dans ce cas, la probabilité demandée est:

P (a│b^C) = 0.03/0.17 = 0.1765

Les références

1. Canavos, g. 1988. Probabilité et statistiques: applications et méthodes. McGraw Hill.
2. Devore, J. 2012. Probabilité et statistiques pour l'ingénierie et la science. 8e. Édition. Cengage.
3. Lipschutz, s. 1991. Série Schaum: probabilité. McGraw Hill.
4. Obregón, je. 1989.Théorie de la probabilité. Limusa éditorial.
5. Walpole, R. 2007. Probabilité et statistiques pour l'ingénierie et la science. Pearson.
6. Wikipédia. Probabilité conditionnée. Récupéré de: est.Wikipédia.org.