Prisme heptagonal

Qu'est-ce qu'un prisme heptagonal?

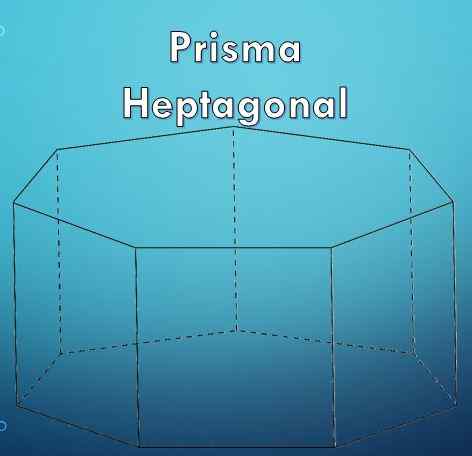
UN prisme heptagonal C'est une figure géométrique qui, comme son nom l'indique, implique deux définitions géométriques qui sont: Prism et Heptagon. Un "prisme" est une figure géométrique limitée de deux bases qui sont des polygones égaux et parallèles et leurs faces latérales sont des parallélogrammes.

Un "heptagone" est un polygone formé par sept (7) côtés. Puisqu'un heptagone est un polygone, il peut devoir être régulier ou irrégulier.

Un polygone serait régulier si tous leurs côtés ont la même longueur et que leurs angles internes mesurent les mêmes, ils sont également appelés polygones équilatéraux; Sinon, on dit que le polygone est irrégulier.

Caractéristiques d'un prisme heptagonal

Vous trouverez ci-dessous certaines caractéristiques qui ont un prisme heptagonal tel que: sa construction, les propriétés de ses bases, la zone de tous ses visages et son volume.

1- Construction

Pour construire un prisme heptagonal, deux heptagones sont nécessaires qui seront ses bases et sept parallélogrammes, un de chaque côté de l'heptagone.

Il commence à dessiner un heptagon, puis sept lignes verticales sont tracées, de la même longueur, qui partent de chacun de ses sommets.

Enfin, un autre heptagon est dessiné de telle sorte que ses sommets coïncident avec la fin des lignes tracées à l'étape précédente.

Le prisme heptagonal dessiné auparavant est appelé un prisme heptagonal droit. Mais vous pouvez également avoir un prisme heptagonal oblique comme la figure suivante.

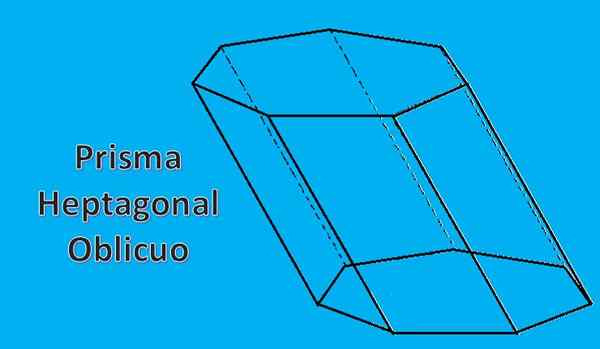
2- propriétés de ses bases

Étant donné que leurs bases sont des heptogons, ils accomplissent que le nombre diagonal est d = nx (n-3) / 2, où «n» est le nombre de côtés du polygone; Dans ce cas, vous devez d = 7 × 4/2 = 14.

Nous pouvons également voir que la somme des angles internes de tout heptagon (régulier ou irrégulier) est le même 900 °. Cela peut être vérifié par l'image suivante.

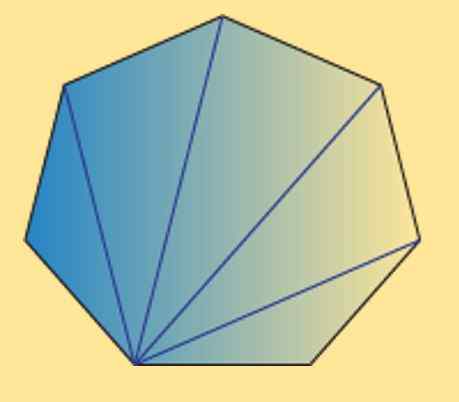
Comme on peut le voir, il y a 5 triangles internes, et en utilisant que la somme des angles internes d'un triangle est égal à 180 °, on peut obtenir que le résultat souhaité.

3- zone nécessaire pour construire un prisme heptagonal

Comme ses bases sont deux heptogons et ses côtés sont sept parallélogrammes, la zone nécessaire pour construire un prisme heptagonal est égale à 2xh + 7xp, où «H» est la zone de chaque heptagon et «p» la zone de chaque parallélogramme.

Dans ce cas, la superficie d'un heptagon ordinaire sera calculée. Pour cela, il est important de connaître la définition de l'apothème.

Apotheme est une ligne perpendiculaire qui va du centre d'un polygone ordinaire au milieu de l'un de ses côtés.

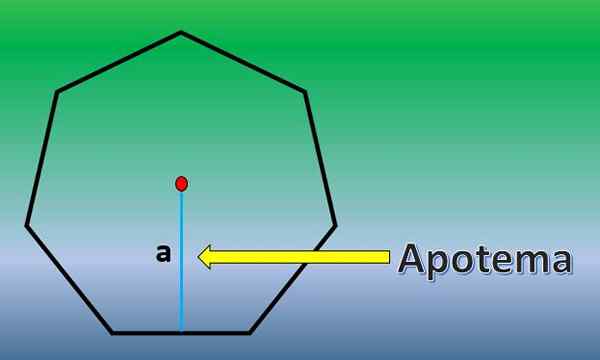
Une fois l'apothéme connu, la zone heptagone est h = 7xlxa / 2, où "l" est la longueur de chaque côté et "a" la longueur de l'apothéme.

La zone d'un parallélogramme est facile à calculer, elle est définie comme p = lxh, où "l" est la même longueur du côté de l'heptagone et "H" est la hauteur du prisme.

En conclusion, la quantité de matériel nécessaire pour construire un prisme heptagonal (avec des bases régulières) est 7xlxa + 7xlxh, c'est-à-dire 7xl (A + H).

4- volume

Une fois la zone d'une base et la hauteur du prisme connu, le volume est défini comme (zone de base) x (hauteur).

Dans le cas d'un prisme heptagonal (avec une base régulière), il doit être v = 7xlxaxh / 2; Il peut également être écrit comme v = pxaxh / 2, où «p» est le périmètre de l'heptagone ordinaire.