Propriétés, éléments, angles, exemples, exemples de polygones réguliers

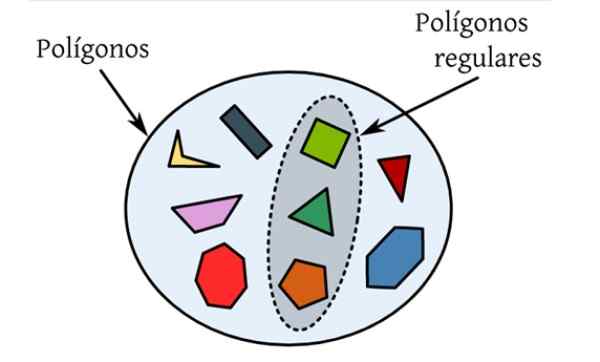
Les polygones réguliers Ce sont ceux qui ont tous leurs côtés et leurs angles internes égaux. Dans la figure suivante, il existe un ensemble de polygones différents, qui sont des chiffres plats limités par une courbe fermée et seuls ceux qui sont mis en évidence répondent aux conditions à être régulières.

Par exemple, le triangle équilatéral est un polygone ordinaire, car ses trois côtés mesurent le même, ainsi que ses angles internes, qui valent 60 º chacun.

Figure 1. Les polygones réguliers sont ceux dont les côtés et les angles internes sont les mêmes, comme le triangle équilatéral et le carré. Source: Wikimedia Commons.

Le carré est un quadrilatère avec quatre côtés à égalité et dont les angles internes sont à 90 °. Il est suivi par le Pentagone ordinaire, avec cinq côtés de taille égale et cinq angles internes de 108º chacun.

Lorsqu'un polygone est régulier, ce mot est ajouté à son nom spécial, nous avons donc l'hexagone ordinaire, l'heptagone ordinaire et ainsi de suite.

[TOC]

Propriétés des polygones ordinaires

Les propriétés les plus importantes des polygones réguliers peuvent être résumées comme suit:

-Les côtés mesurent la même chose, donc ils sont équilatéraux.

-Ils sont Équiagulaire, Eh bien, tous ses angles internes ont une mesure égale.

-Ils peuvent toujours s'inscrire dans une circonférence, ce qui signifie qu'ils s'intègrent parfaitement en un, ce qui est appelé circonférence circonscrite.

-Pour un polygone ordinaire de N côtés, la mesure d'un angle intérieur α est:

α = [180 (n-2)] / n

-N-3) / 2 diagonales peuvent être tirées des sommets d'un polygone, qu'ils soient réguliers ou non.

-La somme de angles extérieurs Il est égal à 360º.

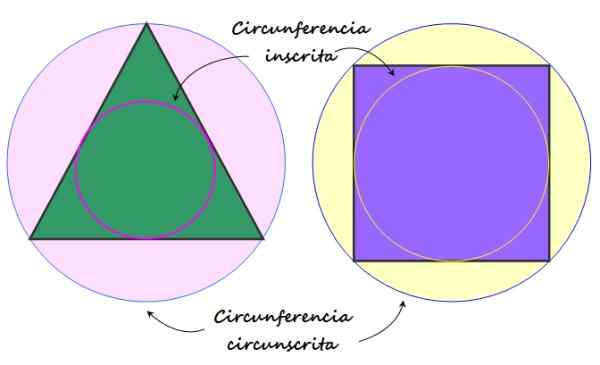Figure 2. Circonférence et circonférence enregistrées circonscrites au polygone ordinaire. Source: F. Zapata.

Éléments d'un polygone ordinaire

Ensuite, nous présentons les principaux éléments d'un polygone ordinaire, visualisé dans la figure inférieure.

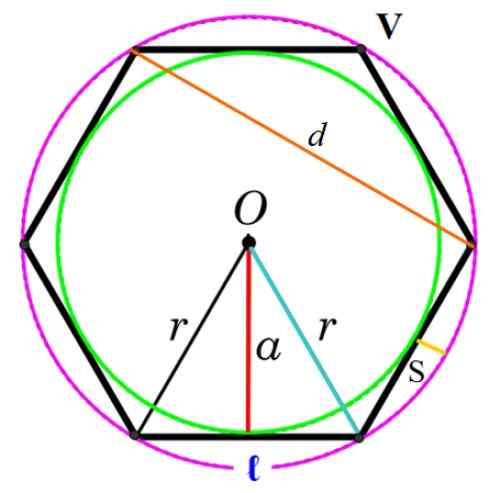figure 3. Éléments du polygone ordinaire. Source: F. Zapata.

Sommet

Le point commun qui a deux côtés consécutifs, désignés V dans la figure.

Côté

C'est le segment qui rejoint deux sommets consécutifs du polygone et est désigné comme ℓ ou L.

Diagonale

Segment qui rejoint deux sommets non consécutifs du polygone, dans la figure, il est désigné comme d.

centre

C'est le centre commun de la circonférence enregistrée et de la circonférence circonscrite, indiquée par la lettre ou. Il peut également être considéré comme le seul point que l'équidista des sommets et des points médians de chaque côté.

Radio

C'est la radio r de la circonférence circonscrite et coïncide avec la distance entre O et un sommet.

Il peut vous servir: axiomes de probabilité: types, explication, exemples, exercices

Apothème

Est appelé apothème au rayon de la circonférence inscrite dans le polygone, représenté dans la figure avec une lettre pour. L'apothème est perpendiculaire sur le côté et unit cela avec le centre O (segment rouge sur la figure 3).

Connaissant le rayon R et la longueur du côté, l'apothème est calculé par:

Puisque, en effet, l'apothem est l'une des catégories d'un triangle rectangle (voir figure 3), l'autre cateto étant la valeur de ℓ / 2 (la moitié d'un côté) et l'hypoténuse la radio r du polygone.

Lorsque le théorème de Pythagore est appliqué audit triangle, cette équation est obtenue, qui est valable non seulement pour l'hexagone, mais pour tout polygone ordinaire.

Angle central

C'est l'angle dont le sommet coïncide avec le centre ou dont les côtés sont les segments qui unissent le centre avec deux sommets consécutifs. Sa mesure dans les degrés Sexagesimal est à 360 ° / N, où n C'est le nombre de côtés du polygone.

Sagita

C'est la différence entre le rayon du polygone et l'apothème (voir figure 3). Indiquant Sagita comme S:

S = R - A

Périmètre et zone

Périmètre

Il est facilement calculé en ajoutant les longueurs des côtés. Comme n'importe quel côté est de la même longueur L et il y a n côtés, le périmètre P est exprimé comme:

P = n.L

Zone

Dans un polygone ordinaire, la zone A est donnée par le produit entre le semi-périmètre (la moitié du périmètre) et la longueur d'apothéme pour.

A = p.A / 2

Comme le périmètre dépend du nombre de côtés n, il s'avère que:

A = (nl).A / 2

Deux polygones réguliers peuvent avoir le même périmètre même s'ils n'ont pas le même nombre de côtés, car cela dépendrait alors de la longueur des côtés.

Dans le livre V de votre Collection, Le mathématicien Pappus d'Alexandrie (290-350), le dernier des grands mathématiciens grecs de l'antiquité, a montré que parmi tous les polygones réguliers avec le même périmètre, celui avec la plus grande zone est celle avec le plus grand nombre de côtés.

Angle

La figure 4 montre les angles pertinents dans un polygone ordinaire, indiqué avec les lettres grecques α, β et γ.

Angle central

Auparavant, nous mentionnons l'angle central, parmi les éléments du polygone ordinaire, c'est l'angle dont le sommet est au centre du polygone et les côtés sont les segments qui unissent le centre avec deux sommets consécutifs.

Pour calculer la mesure de l'angle central α, 360º est divisé par n, le nombre de côtés. Ou 2π radians entre n:

Peut vous servir: fonction injective: de quoi elle consiste, à quoi sert-elle et des exemples

α = 360º / N

Équivalent en radians à:

α = 2π / n

Angle interne ou angle intérieur

Dans la figure 4, l'angle interne β est celui dont le sommet coïncide avec l'une des figures et ses côtés sont également des côtés de la figure. Il est calculé en degrés sexagesimaux par:

β = [180 (n-2)] / n

Ou en radians en utilisant:

β = [π (n-2)] / n

Angles externes

Ils sont désignés par la lettre grecque γ. Dans la figure, il est observé que γ + β = 180º. Donc:

γ = 180º - β

La somme de tous les angles externes à un polygone ordinaire est à 360 °.

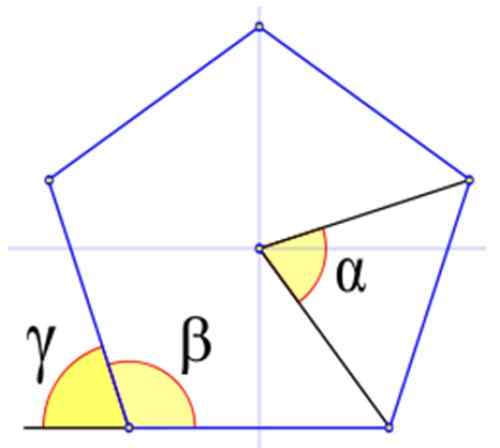Figure 4. Les angles dans un polygone ordinaire, dans cet exemple un pentagone ordinaire. Source: Wikimedia Commons.

Exemples de polygones ordinaires

Ci-dessous, nous avons les 8 premiers polygones réguliers. Nous observons que lorsque le nombre de côtés augmente, le polygone devient de plus en plus à la circonférence dans laquelle ils sont enregistrés.

Nous pouvons imaginer que faire la longueur des côtés de plus en plus petite et augmenter le nombre de ceux-ci, nous obtenons la circonférence.

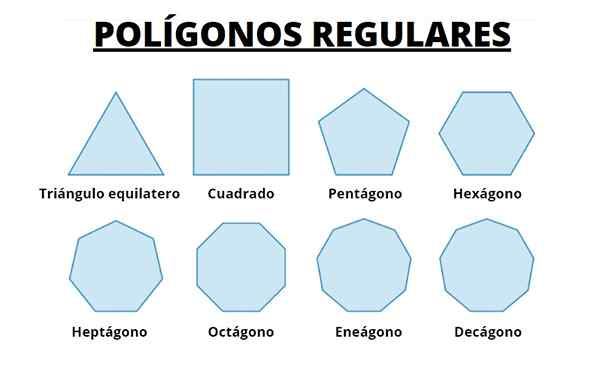Figure 5. Les huit premiers polygones réguliers. Source: Wikimedia Commons.

- Polygones réguliers dans la vie quotidienne et la nature

Des polygones réguliers se trouvent partout dans la vie quotidienne et même dans la nature. Regardons quelques exemples:

Panneaux de signalisation routière

Dans la signalisation, nous voyons sur les autoroutes et les routes abondent des polygones réguliers tels que les triangles équilatéraux, carrés et rhombus. Dans la figure 6, nous voyons un signal à forme élevée.

Figure 5.- Signal de circulation avec forme octogonale. Source: Pixabay.

Meubles

Les innombrables meubles sont carrés par exemple, en tant que figure géométrique caractéristique, ainsi que de nombreuses tables, chaises et banques sont carrées. Un parallélépipe est généralement une boîte avec des côtés en forme de rectangle (qui n'est pas un polygone ordinaire), mais ils peuvent également faire carré.

Architecture et construction

Les carreaux ou les carreaux des sols et des murs, à la fois dans les maisons et dans les rues, ont souvent la forme de polygones réguliers.

Les Tesels sont des surfaces entièrement couvertes de carreaux qui ont diverses figures géométriques. Avec le triangle, le carré et l'hexagone peuvent être fabriqués des voies régulières, celles qui n'utilisent qu'un seul type de figure pour le revêtement parfaitement, sans espaces vides (voir figure 6).

Les bâtiments utilisent également des polygones réguliers dans des éléments tels que les fenêtres et la décoration.

Figure 6. Carreau carré. Source: Pixabay.

- Hexagones ordinaires dans la nature

Étonnamment, l'hexagone ordinaire est un polygone qui apparaît fréquemment dans la nature.

Peut vous servir: distributions discrètes

Les nid d'abeilles préparés par les abeilles pour stocker le miel ont une forme très approximative à un hexagone ordinaire. Comme l'a observé le Pappus d'Alexandrie, de cette façon les abeilles optimisent l'espace pour sauver autant de miel que possible.

Et il y a aussi des hexagones réguliers dans la coquille des tortues et des flocons de neige, qui adoptent également diverses très belles formes géométriques.

Exercice résolu

Un hexagone ordinaire fait partie d'un demi-cercle de rayon de 6 cm, comme le montre la figure. Quelle est la valeur de la zone ombrée?

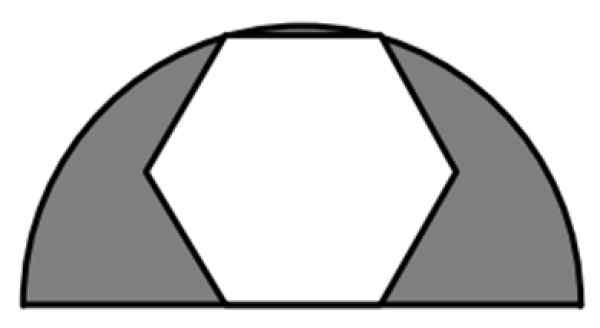Figure 7. Un hexagone ordinaire enregistré en demi-cercle. Source: F. Zapata.

Solution

La zone ombrée est la différence entre la zone de demi-cercle de rayon r = 6 cm et la zone hexagonale complète, un polygone régulier à 6 faces. Nous aurons donc besoin de formules pour la zone de chacune de ces chiffres.

Zone de demi-cercle

POUR₁ = π r² / 2 = π (6 cm)² / 2 = 18π cm²

Zone hexagone ordinaire

La formule pour calculer la surface d'un polygone ordinaire est:

A = p.A / 2

Où P C'est le périmètre et pour C'est l'apothème. Comme le périmètre est la somme des côtés, nous aurons besoin de la valeur de ces. Pour l'hexagone ordinaire:

P = 6ℓ

Donc:

A = 6ℓa / 2

Pour trouver la valeur du côté ℓ, il est nécessaire de construire des chiffres auxiliaires, que nous expliquerons ci-dessous:

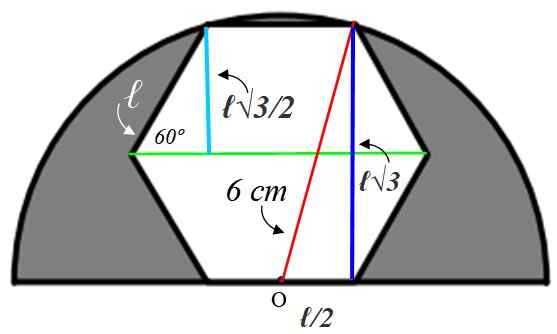
Commençons par le petit triangle rectangle à gauche, dont l'hypoténuse est ℓ. Un angle interne de l'hexagone vaut:

α = [180 (n-2)] / n = α = [180 (6-2)] / 6 = 120º

Le rayon que nous avons tiré en vert bissecta cet angle, donc l'angle aigu du petit triangle est de 60º. Avec les informations fournies, ce triangle est résolu, trouvant le côté bleu clair, qui mesure la même chose que l'apothème:

Cateto opposé = a = ℓ x sin 60º = ℓ√3 / 2 cm

Cette valeur est le double de la jambe bleu foncé du grand triangle à droite, mais à partir de ce triangle, nous savons que l'hypoténuse mesure 6 cm parce que c'est le rayon du demi-cercle. Le cateto restant (ci-dessous) vaut ℓ / 2 depuis le point ou est au milieu du côté.

Étant donné que les angles internes de ce triangle ne sont pas connus, nous pouvons élever le théorème de Pythagore pour lui:

36 = 3 ℓ² + ℓ² / 4

(13/4) ℓ² = 36 → ℓ = √ (4 x36) / 13 cm = 12 / √13 cm

Avec cette valeur, l'apothème est calculé:

a = ℓ√3 / 2 cm = (12 / √13) x (√3 / 2) cm = 6√3 / √13 cm

Appelons un₂ à la zone hexagonale ordinaire:

= 28. 8 cm²

Zone de la figure ombrée

POUR₁ - POUR₂ = 18π cm²  - 28.8 cm² = 27.7 cm²

Les références

1. Baldor, un. 1973. Géométrie et trigonométrie. Éditorial culturel d'Amérique centrale.
2. Profitez des mathématiques. Tesels. Récupéré de: Priematimaticas.com.
3. ET. POUR. 2003. Éléments de géométrie: avec des exercices et une géométrie de la boussole. Université de Medellin.
4. Hexagones dans la nature. Récupéré de: Malvargamath.Wordpress.com.
5. Jiménez, R. 2010. Mathématiques II. Géométrie et trigonométrie. Deuxième édition. Prentice Hall.
6. Polygones réguliers. Récupéré de: mec.ingénierie.USAC.Édu.GT.
7. Wikipédia. Apothème. Récupéré de: est.Wikipédia.org.