Calcul de poids (physique), unités, exemples, exercices

Il lester C'est la force avec laquelle la Terre attire des objets à sa surface. Chaque fois qu'un objet est tombé, cela va au sol, il n'est pas en mesure de gravir ses propres moyens et il ne devient pas ingratissant à mi-chemin, c'est-à-dire que la terre l'attire.

Tous les objets attirent invariablement les uns avec les autres, même les plus petits, seulement que l'ampleur de la force avec laquelle ils font est proportionnelle à la masse. Cela signifie que les objets avec une petite masse exercent peu de force sur les autres, mais les corps célestes comme la Terre sont capables d'exercer une très grande force.

La Terre maintient la lune en orbite autour de lui grâce à cette force d'attraction, qui s'appelle Attraction gravitationnelle En ce qui concerne les objets qui sont loin de la surface de la Terre, et lester Lorsque les objets sont proches.

Cela suit que la force de la gravité ne nécessite pas que les objets soient nécessairement en contact les uns avec les autres pour agir: c'est pourquoi il est dit que c'est une force d'action de distance.

Les objets ont encore du poids même s'ils sont à une certaine hauteur sur le sol et plus.

Le grand scientifique anglais Isaac Newton a été le premier à donner une explication sur cette question, par le biais de la loi universelle de gravitation qui porte son nom et qui depuis lors a servi à comprendre comment les objets interagissent avec la messe avec la messe. C'est très important, car tout objet sur la planète a du poids.

[TOC]

Unités de poids

Le système des unités internationales si le poids du poids est Newton, Nommé en l'honneur d'Isaac Newton. C'est l'unité pour mesurer les forces de toutes sortes.

Le Newton, abrégé n, est défini comme la force nécessaire pour un objet de masse de 1 kg pour acquérir une accélération de 1 m / s². Outre le Newton, il existe d'autres unités de force usagées, par exemple ce qui suit:

Le kilogramme-force

Il kilogramme o Kilopondio, abrégé kg-f ou kp, bien que communément appelé kg sans plus loin. Il est nécessaire de spécifier l'emplacement, car comme indiqué, le champ gravitationnel subit des variations avec la hauteur et la latitude.

Quand quelqu'un dit qui pèse 45 kg, en réalité, ce que cela signifie, c'est que son poids est de 45 kg-F, car le kilogramme est l'unité réservée à la masse.

Peut vous servir: circuit ouvert

L'équivalence entre Kg-F et N est: 1kg-f = 9.8 N

La frontière

La Balance-Fuerza, LB-F abrégé est également une unité de force analogue au KG-F, car c'est la force que la Terre exerce sur un objet de 1 lb de masse. Et comme avec le KG-F, il n'y a aucun problème avec les valeurs lorsque vous êtes sur Terre, c'est-à-dire un objet de masse de masse, pèse 1 lb-f-f.

L'équivalence en lb-f et n est: 1 lb-f ≡ 4.44822 n.

Calcul et formule du poids

Le poids d'un objet est proportionnel à sa masse. Une plus grande masse, plus grand poids.

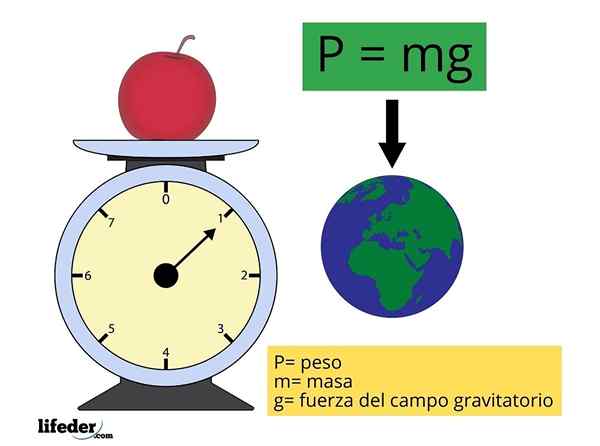
La formule pour trouver l'ampleur du poids p (ou aussi w, comme indique parfois, par "Lester" En anglais) c'est très simple:

P = mg

Où m représente la masse de l'objet et g C'est l'ampleur de l'accélération de la gravité (intensité du champ gravitationnel ou de la gravité), approximativement constant et dont la valeur est prise comme 9.81 m / s² Pour les calculs les plus fréquents.

Le poids est un vecteur et pour distinguer un vecteur et son ampleur, les lettres audacieuses sont utilisées. De cette façon, lorsque vous parlez de P, il est entendu que c'est la valeur numérique et quand il est écrit P Une référence est faite au vecteur:

P = m ∙g

La g Avec des paroles audacieuses, c'est le champ gravitationnel terrestre, c'est-à-dire l'influence que la Terre exerce sur l'espace qui l'entoure, qu'il y ait ou non un autre corps qui le perçoit ou non. Tout objet avec masse a son propre champ gravitationnel, qu'il soit petit ou grand.

L'intensité du champ gravitationnel terrestre g Ce n'est pas entièrement constant. Il a de petites variations qui surviennent principalement parce que la Terre n'est pas une sphère parfaite et aussi aux différences locales de hauteur et de densité locales. Mais pour la plupart des applications, valeur 9.81 m / s² Il fonctionne très bien.

D'autres corps célestes ont leur propre champ gravitationnel caractéristique, donc l'accélération de la gravité diffère selon la planète ou le satellite. Le même objet aurait un poids différent dans chacun, donc le poids n'est pas une propriété caractéristique des choses, mais du sujet en général.

Le poids en tant que vecteur

Le poids est un vecteur et a donc l'ampleur, la direction et le sens. À proximité de la surface de la Terre, le poids est un vecteur vertical et la direction est toujours en panne.

En général, l'adresse verticale est nommée axe et soit z, Et le sens est assigné signe + ou signe - pour le distinguer de la direction vers le haut. Le choix dépend de l'emplacement de l'origine. Dans l'image inférieure, l'origine a été choisie au point à partir duquel la pomme tombe:

Peut vous servir: gaz idéal: modèle, comportement, exemples Le poids est un vecteur dirigée verticalement. Source: F. Zapata.

Le vecteur unitaire J, Un vecteur de grandeur égal 1, est utilisé pour pointer et distinguer la direction verticale. En termes de ce vecteur, le poids est écrit comme ceci:

P = mg (- J)

Où le signe négatif est affecté à la direction.

Différences entre le poids, la masse et le volume

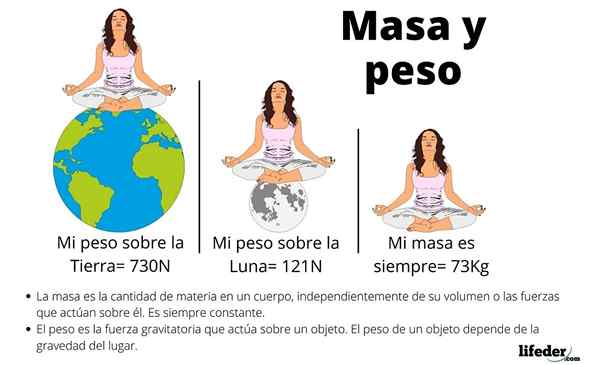
Souvent, ces trois concepts sont confus, mais en examinant les caractéristiques du poids, il est facile de le différencier de la masse et du volume.

Pour commencer, le poids dépend du champ gravitationnel de l'endroit où l'objet est. Par exemple, sur terre et sur la lune, la même chose ait un poids différent, bien que la quantité d'atomes qui le composent est constante.

La masse est une ampleur scalaire, liée à la quantité d'atomes qui composent l'objet et est attirée par la résistance que l'objet doit changer son mouvement, une propriété appelée inertie.

Pour sa part, le volume est la mesure de l'espace occupé par un objet, une autre quantité scalaire. Deux objets avec un volume égal ne pèsent pas le même, par exemple un cube de fer pèse bien plus qu'un autre polystyrène des mêmes dimensions.

En résumé:

• La masse est liée à la quantité de matière d'un corps.
• Le poids est la force exercée par la terre sur cette masse, proportionnelle à elle.
• Le volume est l'espace occupé par la matière.

Il convient de noter que les quantités scalaires, ni la masse ni le volume n'ont de direction ou de signification, mais seulement une valeur numérique et une unité adéquate. D'un autre côté, le poids, étant un vecteur, doit toujours être exprimé correctement en soulignant l'ampleur, l'unité, la direction et le sens, comme dans la section précédente.

Exemples de poids

Tous les objets sur terre ont du poids, vous pouvez même "peser" des objets qui ne sont pas sur Terre, comme les autres planètes ou le soleil, bien que par des moyens indirects, bien sûr.

Comme la plage de poids est très grande, une notation scientifique est utilisée (en puissances de 10) pour en exprimer certaines qui sont très grandes ou très petites:

-Le soleil: 1 989 × 10³⁰ kg-f

-Jupiter: 1 898 × ​​10²⁷ kg-f

-Un moustique: 2.0 × 10^-5 N

-Bébés: 34.3 N

-Un enfant: 353 n

-Personne adulte: 65 kg-f

-Un éléphant adulte: 5.5 × 10³ kg-f

-Baleine bleue: 1.0 × 10⁶ N

Exercice résolu

Une boîte de pâte 20 kg repose sur une table.

a) Trouvez le poids de la boîte et la force normale que la table exerce dessus.

Peut vous servir: conservation de l'élan linéaire: principe, exemples, exercices.

b) Une autre boîte de 10 kg est placée sur le premier. Trouvez celui normal que le tableau exerce sur la boîte de 20 kg et celui normal qu'il exerce sur la plus petite boîte.

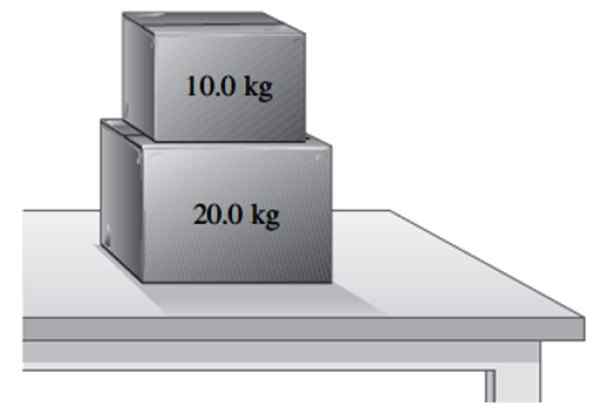Deux boîtes reposant sur une table. Source: F. Zapata.

Solution à

Il est pratique de créer un diagramme corporel libre sur la boîte, qui consiste à dessiner les forces agissant dessus.

Dans cette situation, il y a toujours la plus petite boîte sur le dessus, donc il n'y a que deux forces: le premier est le poids P qui est dessiné verticalement vers le bas, comme indiqué dans les sections précédentes et ensuite il y a la normale N, qui est la force perpendiculaire que le tableau exerce et empêche la boîte de tomber.

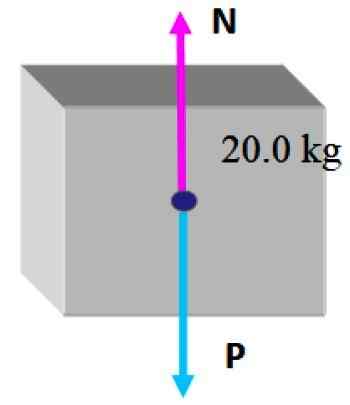
Étant donné que la boîte est en équilibre statique dans ces circonstances, il est raisonnable de conclure que l'ampleur de la normale est la même que celle du poids, afin qu'elle puisse compenser: par conséquent:

N = mg = 20.0 kg x 9.8 m / s² = 196 N; réalisé verticalement.

Pour sa part, le poids est P = 196 N dirigé verticalement.

Solution B

Maintenant, de nouveaux diagrammes de corps libres sont fabriqués sur les deux objets. Pour la grande boîte, les choses changent un peu, car la petite boîte exerce de la force dessus.

Les forces sont les suivantes: N et P Ils sont respectivement le normal que la table exerce et le poids sur la boîte de 20.0 kg, cela n'a pas changé. Et la nouvelle force exercée par la petite boîte est N₁, la normale due au contact avec la face supérieure de la grande boîte.

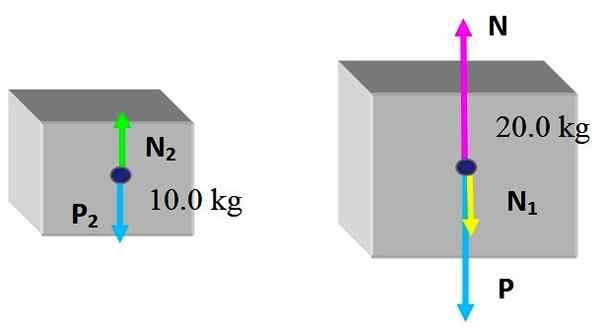
Quant à la petite boîte, elle reçoit la normale N₂, exercé par la face supérieure de la grande boîte et bien sûr son poids P₂. Puisque les cases sont un équilibre statique:

N₂ - P₂ = 0

N - n₁ - P = 0

De la première équation, vous devez n₂ = P₂ = 10 kg x 9.8 m / s² = 98 N. Par la loi d'action et de réaction, l'ampleur de la force que la petite boîte reçoit est la même qu'elle exerce sur la grande boîte, puis:

N₂ = N₁ = 98 N

De la deuxième équation, la normale N que la table exerce sur la grande boîte est effacée, ce qui a à son tour la petite boîte sur le dessus:

N = n₁ + P = 98 n + 196 n = 294 n

Les références

1. Figueroa, D. 2005. Série: Physique pour la science et l'ingénierie. 2ieme volume. Dynamique. Édité par Douglas Figueroa (USB).
2. Giambattista, un. 2010. La physique. 2e. Élégant. McGraw Hill.
3. Giancoli, D.  2006. Physique: principes avec applications. 6e. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1. Pearson.
5. SERAY, R., Jewett, J. 2008. Physique pour la science et l'ingénierie. Volume 1. 7e. Élégant. Cengage Learning.
6. Thomas Griffith, W. 2007. Physique conceptuelle. Mc Graw Hill.