Y = 3sen (4x) période de fonction

Il Y = 3sen (4x) période de fonction C'est 2π / 4 = π / 2. Pour comprendre clairement la raison de cette déclaration, la définition d'une période de fonction et de la période de la fonction Sen (x) doit être connue; Un peu sur les fonctions Graph sera également utile.

Les fonctions trigonométriques, telles que les sinus et le cosinus (Sen (x) et COS (x)), sont très utiles à la fois en mathématiques et en ingénierie.

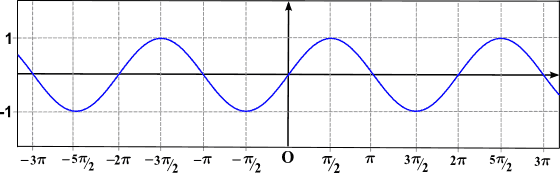
Le mot période mentionne la répétition d'un événement, donc dire qu'une fonction est périodique équivaut à dire "son graphique est la répétition d'une courbe". Comme on peut le voir dans l'image précédente, la fonction Sen (x) est périodique.

Fonctions périodiques

Une fonction f (x) est dirigée périodique s'il y a une valeur réelle p ≠ 0 telle que f (x + p) = f (x) pour tous les x dans le domaine de la fonction. Dans ce cas, la période de la fonction est p.

Il est généralement appelé une période de la fonction au nombre réel positif le plus bas P qui satisfait la définition.

Comme on peut le voir dans le graphique précédent, la fonction Sen (x) est périodique et sa période est 2π (la fonction cosinus est également périodique, avec une période égale à 2π).

Modifications du graphique d'une fonction

Soit f (x) une fonction dont le graphique est connu, et être une constante positive. Qu'arrive-t-il au graphique de f (x) si multiplie f (x) par c? En d'autres termes, comment est le graphique de C * f (x) et f (cx)?

C * f graphique (x)

En multipliant une fonction, à l'extérieur, par une constante positive, le graphique de f (x) subit un changement dans les valeurs de sortie; Autrement dit, le changement est verticalement et que deux cas peuvent être pris:

- Si C> 1, alors le graphique souffre d'un étirement vertical avec un facteur C.

- Oui 0

F graphique (CX)

Lorsque l'argument d'une fonction est multiplié par une constante, le graphique de f (x) subit un changement dans les valeurs d'entrée; Autrement dit, le changement est horizontalement et, comme avant, deux cas peuvent être pris:

- Si C> 1, alors le graphique souffre d'une compression horizontale avec un facteur de 1 / c.

- Oui 0

Y = 3sen (4x) période de fonction

Il convient de noter que dans la fonction f (x) = 3se (4x), il y a deux constantes qui modifient le graphique de la fonction sinusale: une multipliez externe et une autre de manière interne.

Le 3 qui est en dehors de la fonction sinus est d'étendre la fonction verticalement par un facteur 3. Cela implique que le graphique de la fonction 3SEN (x) sera entre les valeurs -3 et 3.

Le 4 qui se trouve dans la fonction sinus.

D'un autre côté, la période d'une fonction est mesurée horizontalement. Comme la période de la fonction Sen (x) est de 2π, lors de la considération du péché (4x), la taille de la période changera.

Pour savoir quelle est la période de y = 3sen (4x) multiplier juste la période de la fonction Sen (x) de 1/4 (le facteur de compression).

En d'autres termes, la période de la fonction y = 3sen (4x) est 2π / 4 = π / 2, comme on peut le voir dans les derniers graphiques.