Éléments pentadecágono, classification, caractéristiques, exercice

UN Pentadecantaillement C'est une figure plate construite avec quinze segments droits et à fermer. Ce type de figures est appelé polygone et ils sont nommés selon la quantité de côtés qui ont.

Le triangle, avec trois côtés et le quadrilatère, de quatre, sont des exemples de polygones très familiers, mais les polygones peuvent avoir plus de côtés.

Figure 1.  Pentagone régulier avec des sommets rouges. Source: Wikimedia Commons.

Les éléments de base du pentadecágono sont les mêmes que n'importe quel polygone, quelle que soit la quantité de côtés qu'il possède. Ces éléments sont:

-Côtés, qui sont les segments qui composent le Pentadecágono pour un total de 15.

-Sommets, également 15, qui sont les extrémités des côtés adjacents.

-Angles internes, Ceux qui se forment dans le pentadecágono entre deux côtés adjacents.

-Angles externes, formé entre un côté et la prolongation de l'un des côtés consécutifs.

-Diagonales, Les segments de ligne qui rejoignent deux sommets non adjacents.

[TOC]

Classification

Un pentadecágono peut être régulier soit irrégulier, en fonction de la taille de leurs côtés et de la mesure de ses angles internes. Si vous avez tous les côtés et les angles internes égaux -quilátero et equiangle - il est régulier, comme le montre la figure 1, sinon il est irrégulier.

Il peut également être classé comme convexe soit concave. Un pentagone concave a un ou plusieurs angles internes supérieurs à 180º, tandis que l'on a toujours convexe a des angles internes inférieurs à 180 °. Le pentagone ordinaire est convexe.

Un autre critère de classification est considéré si ses côtés non consécutifs - ou leurs extensions - sont coupés ou non. Quand ils ne sont pas coupés, comme dans le cas de la figure 1, on dit que c'est un simple pentadecágon. Et s'ils sont coupés, alors c'est complexe.

Il peut vous servir: géométrie analytique

Le pentagone ordinaire

Le pentagone ordinaire, dont les côtés et les angles internes ont la même mesure, est une figure d'une grande symétrie, car les éléments supplémentaires suivants sont définis à ceux décrits précédemment:

-centre: Le point que l'équidista des sommets et des côtés.

-Radio: La distance entre le centre et l'un des sommets réguliers du Pentagone.

-Angle central: Celui qui a son sommet au centre de la figure et ses côtés passent à travers deux sommets adjacents.

-Apothème, C'est le segment perpendiculaire qui rejoint le centre d'un côté avec le centre de la figure.

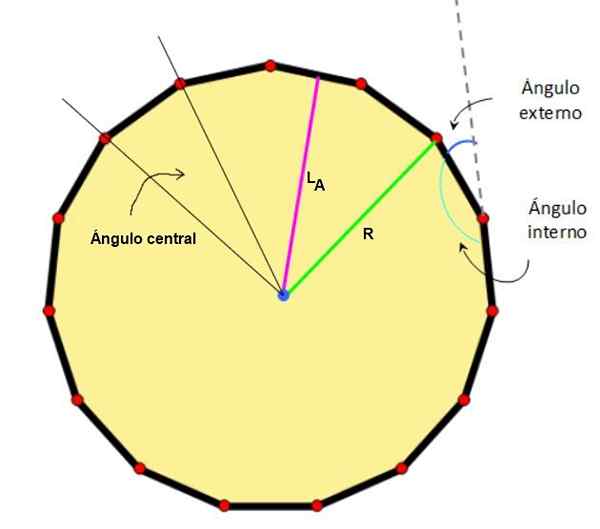Figure 2. Centre, apothème, radio et angles notables d'un pentadecágono. Source: Wikimedia Commons / F. Zapata.

- Caractéristiques du pentagone ordinaire

Angles internes

La formule suivante est utilisée pour calculer la mesure I des angles internes de tout polygone ordinaire, où n C'est le nombre de côtés:

Dans cette formule, la mesure où je suis en degrés, pour l'exprimer en rayons, il est multiplié par le facteur π / 180. Voyons quelle est la mesure des angles internes du Pentagone ordinaire, remplaçant n = 15:

I = [(15-2) × 180º] / 15 = 156º

Équivalent à 13π / 15 radians. Étant donné que les angles internes du Pentagone ordinaire sont inférieurs à 180 °, c'est un polygone convexe.

Somme des angles internes

Il est possible de calculer la somme des angles internes par la formule suivante:

S = (n-2) x 180º

Comme toujours, n représente le nombre de côtés. Cette formule est valable pour n = 3, 4, 5 .. .

Faire n = 15 nous obtenons:

S = (15 - 2) x 180º = 2340º

Angles externes

Un angle interne et un angle externe sont supplémentaires, c'est-à-dire que sa somme est de 180 °, comme indiqué dans la figure 2. Par conséquent, un angle externe des mesures de Pentadecágono:

Peut vous servir: Binôme conjugué: comment il est résolu, exemples, exercices

180 º - 156º = 24º.

Périmètre et zone

Le périmètre est la mesure du contour du polygone et ajoute facilement tous les côtés. Ouais pour C'est la longueur du côté, il suffit de se multiplier par n, Le nombre de côtés.

Pour un pentagone ordinaire de côté A, le périmètre P est:

P = 15A

S'il s'agit d'une figure irrégulière, dans laquelle diffère la mesure des côtés, le périmètre ajoute la longueur de tous ses côtés.

Quant à la zone, nous pouvons le calculer de plusieurs manières. Par exemple, nous avons la formule qui vous permet de l'obtenir en connaissant la longueur de ses côtés:

Effectuer les opérations indiquées, elle reste approximativement:

A = 17 6426⋅a²

Il existe une autre option, applicable aux polygones ordinaires. Il s'agit de les diviser en triangles de base égaux au polygone à. La hauteur du triangle est la longueur de l'apothem L_POUR, défini ci-dessus.

La zone dudit triangle est calculée avec la formule bien connue: Base x hauteur / 2. De cette façon, la zone de triangle unique est:

Zone = A. L_POUR / 2

Pour avoir la surface totale du polygone, il suffit de se multiplier par le nombre de côtés n, qui dans ce cas est de 15:

A = 15⋅a⋅ L_POUR / 2

Et puisque le périmètre de la figure est p = 15⋅a, alors:

A = p⋅ l_POUR / 2

Diagonales

Les diagonales sont les segments qui unissent deux sommets non consécutifs, comme indiqué ci-dessus. Pour savoir combien de diagonales un polygone ordinaire a de n côtés, y compris Pentadecágono, il y a la formule suivante:

Où d est le nombre de diagonales.

Maintenant, nous remplaçons n = 15, pour obtenir les diagonales totales:

Peut vous servir: polygones réguliers: propriétés, éléments, angles, exemples

D = [15 × (15-3)] / 2 = 90 diagonales.

Construction avec règle et boussole

Pentadecágono est construit avec une règle et une boussole à partir d'une circonférence. Le 360º doit être divisé en 15 parties égales de 24º chacune. D'abord les constructions auxiliaires indiquées dans l'animation sont effectuées pour obtenir un angle de 60º, qui est divisé à son tour en 36º et 24º.

figure 3. Construction avec règle et boussole d'un Pentagone ordinaire. Source: Wikimedia Commons.

Exercice résolu

Si le périmètre d'un pentadecágono enregistré dans un cercle de rayon R est de 12,56 cm. Calculer:

a) la radio.

b) Votre région.

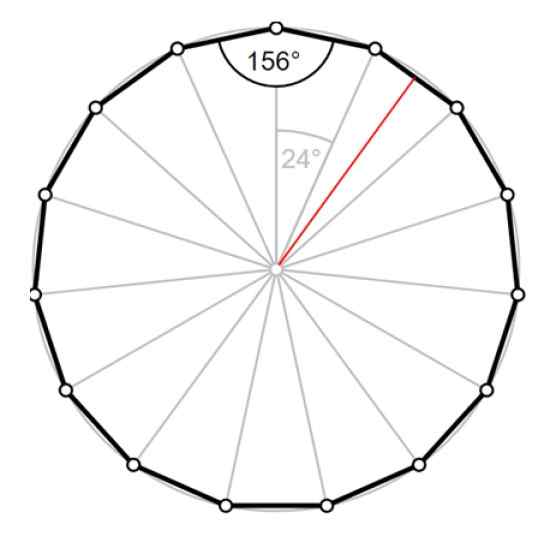Figure 4. Pentadecágono: angle central, angle interne et apothéma rouge. Source: Wikimedia Commons / F. Zapata.

Solution à

Le périmètre est p = 15⋅a = 12.56 cm, donc le côté de pentadecágono est 0.8373 cm. La radio Nous pouvons le calculer à l'aide de l'un des triangles de la figure 4.

L'apothème L_POUR correspond à la hauteur du triangle, dessinée en rouge, qui divise l'angle de 24º en deux angles de 12º chacun.

Il y a deux triangles droits avec un angle interne de 12º chacun, et à l'un d'eux, nous pouvons appliquer la trigonométrie pour trouver l'hypoténuse, qui est la longueur R du rayon.

De cette manière:

sen 12º = (a / 2) / r

R = (a / 2) / sen 12º = (0.8373 cm / 2) / sen12º = 2.01 cm.

Solution B

Nous pouvons calculer la région de Pentadecágono à l'aide de la formule:

A = p⋅ l_POUR / 2

Nous connaissons déjà le périmètre p = 12.56 cm, et la longueur de l'apothème est calculée par la tangente ou le cosinus à 12 °:

Cos 12º = L_POUR / R

L_POUR = R. cos 12 º = 2.01 cm. cos 12 º = 1.97 cm

Remplacement:

A = 12.56 cm⋅ 1.97 cm / 2 = 12.35 cm²

Les références

1. Alexander, D. 2013. Géométrie. 5e. Édition. Cengage Learning.
2. Apprenez les mathématiques. Figures géométriques. Récupéré de: Rodrigoanchorerena.Wixsite.com.
3. Mathématiques de Sangaku. Éléments d'un polygone et de sa classification. Récupéré de: Sangakoo.com.
4. Wikipédia. Pentadecágono. Récupéré de: est.Wikipédia.org.
5. Monde mathématique Wolfram. Pentadecagon. Récupéré de: Mathworld.Wolfram.com.