Pascalina ou Pascal Machine

Nous expliquons ce qu'est la Pascalina, son histoire, ses caractéristiques et son fonctionnement

Pascal de Pascal (1652). Source: Rama, CC BY-SA 3.0 fr, via Wikimedia Commons

Qu'est-ce que Pascalina?

La Pascalina Il s'agit d'une calculatrice mécanique, créée par le scientifique et philosophe français Blaise Pascal (1623-1661), vers 1642, avec seulement 19 ans. Le nom "Pascalina" a été donné en son honneur, bien qu'il s'appelle également "machine arithmétique".

Grâce à un système d'équipement fait de fer et soigneusement articulé, Pascalina est capable d'ajouter et de soustraire, étant ainsi le précurseur des calculatrices actuelles. Et tout comme ceux-ci, Pascalina a une interface pour l'entrée de données qui, au lieu des clés, utilise une série de disques rotatifs numérotés, pour indiquer la valeur de position de chaque chiffre: unités, dizaines, centaines et plus.

Les disques numérotés sont fournis avec des trous, dans lesquels une tige ou un stiletto est introduit pour les transformer par étapes.

Le mécanisme interne se compose d'une série de roues à dents couplées délicatement, qui se déplacent, étape par étape, cylindres avec deux jeux de nombres de 0 à 9. Certaines fenêtres situées sur les disques, permettent d'observer les valeurs que ces nombres acquièrent, lors de la réalisation d'une sous-conservation ou d'une opération de soustraction.

Histoire

Depuis son enfance, Pascal avait déjà démontré ses grandes compétences intellectuelles, alors son père, magistrat et mathématicien Etienne Pascal, a décidé de lui donner la meilleure éducation possible. En 1642, Etienne Pascal a été envoyée pour augmenter les impôts à Rouen, Normandie, au nord de la France, une œuvre qui n'était pas facile.

Blaise Pascal, déterminée à aider son père, a conçu et construit une machine qui, en utilisant des engrenages mécaniques, a pu faire pivoter des roues pour effectuer et montrer les opérations des sommes et de la soustraction. Cet appareil a été appelé "Pascalina".

Blaise Pascal

Avec Pascalina, les multiplications et les divisions peuvent également être effectuées, mais pas directement, mais par des sommes successives et de la soustraction.

Peut vous servir: le jour sidéréal ou sidereh

Le coût de la fabrication de Pascalina était cependant très élevé, donc l'invention est passée inaperçue à la majorité à ce moment-là. Ceux qui pourraient se permettre un, ont préféré le laisser à la maison et ne pas l'utiliser pour un travail de routine, donc presque tout le monde a continué à résoudre ses opérations de la manière traditionnelle.

Le mécanisme de Pascalina devrait être très précis, de sorte que la calculatrice a fonctionné correctement, mais a souvent cessé de fonctionner. Et Pascal était le seul à pouvoir le réparer à chaque fois que cela se produisait.

Pascal a continué d'améliorer sa conception au cours des 10 prochaines années, atteignant environ 50 Pascalinas, dont deux sont conservées: l'une est en Allemagne, au Zwinger Museum, à Dresde, en Allemagne, et une autre dans la Musée des Arts et Métiers, à Paris, à Paris.

Caractéristiques et fonction de la Pascalina

Pascalina a des caractéristiques communes aux calculatrices d'aujourd'hui, comme indiqué au début. La différence évidente est que Pascalina travaille avec des éléments mécaniques, dont l'ajustement doit être parfait, tandis que les calculatrices d'aujourd'hui fonctionnent par électronique.

Fondamentalement, Pascalina a:

• Une interface pour saisir les données, composée de cadrans exploités par un stiletto.
• Le mécanisme interne utilisé pour traiter ces données, en fonction des engrenages et des dentas mobiles.
• Un panneau qui montre les résultats, avec des fenêtres d'enregistrement, pour apprécier le mouvement introduit dans les cadrans et observer les résultats.

Les sommes sont effectuées directement, en déplaçant les cadrans pour introduire chaque chiffre des ajouts. Cependant, la soustraction n'est pas réalisée directement, mais d'une manière qui, en principe, est assez curieuse: le complément de Pascalino, qui est expliqué ci-dessous:

Complément au complément 9 ou pascalino

Le complément à 9 est une technique numérique qui convertit les soustractions en somme, plus facile à résoudre avec le système mécanique mis en œuvre par Pascal.

Peut vous servir: diagramme de flux

Par exemple, si vous souhaitez résoudre l'opération A - B, il ajoute «A» avec le complément Pascalino de «B», et le résultat de cette opération est la soustraction recherchée.

Il est d'abord expliqué comment trouver le complément à 9 de n'importe quel nombre n. Il est très simple, il est soustrait de 9 chaque chiffre de ce nombre, comme indiqué dans les exemples suivants:

• Soit n = 20, son complément à 9 fait: 99 - 20 = 79
• Pour n = 347, vous devez faire: 999 -347 = 652
• Si n = 7, son complément à 9 est 2.

Soustractions par complément à 9

Maintenant, supposons que vous souhaitiez effectuer l'opération suivante:

1246 - 822

Les étapes suivantes sont suivies:

Étape 1: Trouvez le complément à 9 des volés, qui est de 822, qui est 999 - 822 = 177.

Étape 2: Effectuez la somme du Minuend et le complément à 9 précédemment trouvés: 1246 + 177 = 1423, observez bien à gauche dans le résultat du résultat.

Étape 3: L'opération de soustraction demandée est 423 + 1 = 424.

Le lecteur peut vérifier le résultat avec une calculatrice commune!

Si le MinUend est inférieur à la soustraction, procédez, par exemple, pour effectuer:

267 - 592

Étape 1: Trouvez le complément à 9 du paragraphe 592, qui est 999 - 592 = 407.

Étape 2: Ajouter MinUend et complément à 9 des volés: 267 + 407 = 674.

Étape 3: Calculer le complément à 9 du résultat: 999 - 674 = 325

Étape 4: Ajoutez le signe négatif au résultat: -325 et c'est la soustraction demandée.

À première vue, il semble plus compliqué de faire une soustraction de cette manière, mais avec le système de roues denté, il est plus facile.

Comment fonctionne Pascalina?

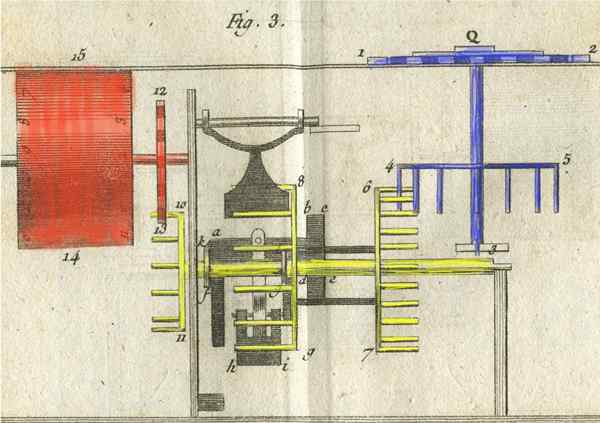
Mécanisme interne de la Pascalina

Pascalina se compose essentiellement d'un système de vitesse qui fait pivoter 10 cylindres qui indiquent les nombres. Chaque cylindre rassemble deux séries de nombres, et chaque série passe de 0 à 9.

Le cylindre de l'extrême droite indique les unités, qui suit les dizaines, les centaines suivantes et ainsi de suite. Lorsque l'un des cylindres tourne un virage complet, le mécanisme fait celui de votre avance gauche. Plus la figure a des chiffres, plus ils doivent déplacer de roues et de cylindres, ce qui donne une idée du délicat du mécanisme interne de la Pascalina.

Peut vous servir: 11 exemples de recherche sur le terrain

L'entrée des numéros est effectuée via les cadrans numérotés à l'extérieur de l'appareil, avec une aiguille ou un stiletto, conçu à cet effet. Il y a des cadrans pour les unités, les dizaines, les centaines et plus, correspondant à chacun des cylindres.

Maintenant, vous verrez comment effectuer les opérations.

Ajouter

Supposons que vous souhaitiez faire l'opération suivante avec une Pascalina:

25 + 14

Avec tous les cadrans initialisés en 0, le cadran des dizaines 2 unités ou étapes se déplace, et le cadran des unités se déplace en 5 étapes. Avec cela, le premier ajout est introduit.

Puis le cadran de l'unité Tens 1 se déplace, et celui des unités à 4. Le résultat est: 39.

Lorsqu'un virage complet est pris à 8 et que les roues ajoutent les tours nécessaires aux engrenages des chiffres supérieurs, pour montrer le résultat.

Soustraire

Pour soustraire, tous les cadrans sont placés à 9, car le mécanisme affecte la soustraction par complément à 9, comme indiqué dans la section précédente. L'utilisateur n'a pas à calculer le complément, le mécanisme le fait seul, en initialisant les DAL par 9.

Par exemple, vous voulez faire:

67 - 21

Il se déroule de la même manière que dans la somme, c'est-à-dire que le cadran des dizaines est tourné en 6 étapes et celui des unités est tourné en 7 étapes. De cette façon, la valeur du Miniend est introduite. Ensuite, le cadran des dizaines 2 étapes et celui des unités 1 est tourné. Le résultat est 46, comment le lecteur peut-il vérifier.