La notation a développé ce qui est, des exemples et des exercices
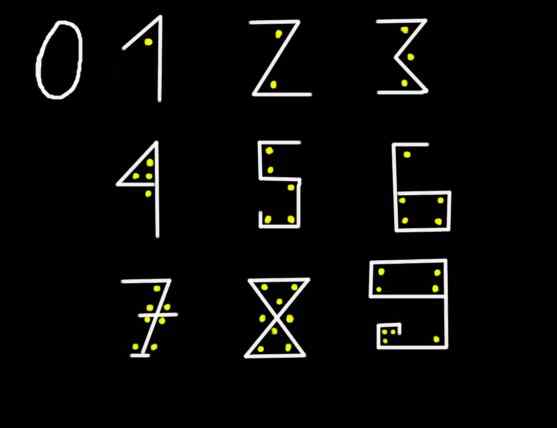
- 2321
- 178
- Eva Henry
La notation développée C'est celui dans lequel une figure numérique est exprimée comme une somme dans laquelle la valeur de position de chaque chiffre qui forme le nombre est prise en compte.
Par exemple, lors de l'écriture d'une figure comme 2345 chaque chiffre a une hiérarchie positionnelle. Lecture du chiffre extrême droit vers la gauche, la hiérarchie ou la valeur augmente.
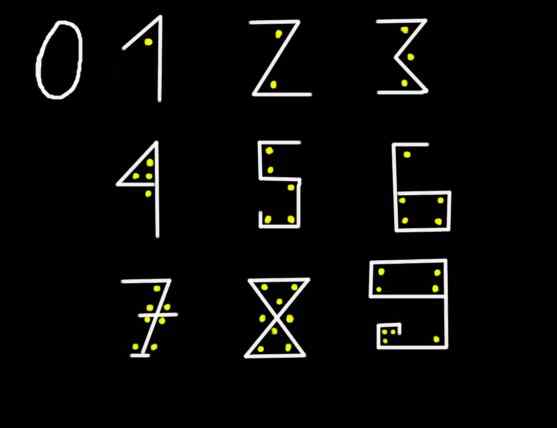 Figure 1. Avec neuf graphimes, il est possible de représenter n'importe quelle figure.
Figure 1. Avec neuf graphimes, il est possible de représenter n'importe quelle figure. Dans la figure 2345, le chiffre 5 représente cinq unités, le chiffre 4 représente quatre dizaines, le 3 correspond à la troisième position de gauche à droite et donc le 3 représente trois cents, finalement le 2 représente deux mille mille. Autrement dit, en notation développée ou étendue, la figure 2345 est écrite comme celle-ci:
2345 = 2 mille + 3 cent + 4 dizaines + 5 unités
Mais il peut également être exprimé comme suit:
2345 = 2 x 1000 + 3 x 100 + 4 x 10 + 5 x 1.
La figure 2345 peut également être écrite comme la somme des pouvoirs de 10:
2345 = 2 x 10 ^ 3 + 3 x 10 ^ 2 + 4 x 10 ^ 1 + 5 x 10 ^ 0
Où le circonflejo ^ signifie élever l'exposant indiqué. Par exemple, 10 ^ 3 = 10 x 10 x 10 = 1000. Une autre façon d'écrire les représentants est par une supervision:
2345 = 2 x 103 + 3 x 102 + 4 x 101 + 5 x 100
[TOC]
Système de numérotation de position
Le système de numéros arabes est les chiffres qui sont utilisés quotidiennement dans la grande majorité des continents et des pays du monde. Les nombres arabes sont un système de base 10 car dix symboles ou graphiques sont utilisés pour écrire n'importe quel numéro. Ces dix symboles sont:
0 1 2 3 4 5 6 7 8 9
Avec un seul de ces symboles, des chiffres entre zéro à neuf peuvent être exprimés. Pour exprimer des chiffres supérieurs à neuf, le système positionnel basé sur dix. La figure 10 est une douzaine et zéro unités. La figure 11 est une douzaine et une unité. La figure 123 (cent vingt-trois) est cent, deux dizaines et trois unités. Écrit sous forme de pouvoirs de dix, le numéro 123 sera:
Peut vous servir: 60 diviseurs1 × 10 ^ 2 + 2 × 10 ^ 1 + 3 × 10 ^ 0
Où:
10 ^ 2 = 10 x 10 = 100
10 ^ 1 = 10
10 ^ 0 = 1.
Avec cet exemple, il est clair que la position du chiffre à la fin est la position 0 et représente le nombre d'unités, celle du deuxième chiffre de droite à gauche est la position 1 et représente le nombre de dizaines, le troisième chiffre (droit à la gauche) a la position 2 et représente les centaines.
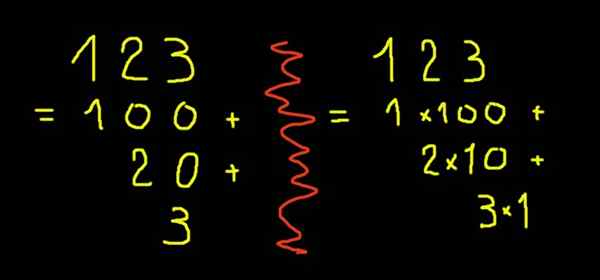 Figure 2. Notation développée de la figure 123.
Figure 2. Notation développée de la figure 123. Nombres fractionnaires ou décimaux
Avec le système de position décimal, il est également possible.
Pour représenter la fraction ½ dans le système décimal arabe, c'est-à-dire la moitié de l'unité est écrite:
½ = 0,5
Pour atteindre cette expression dans notre système en fonction de 10, les opérations suivantes ont été effectuées:
1- Multipliez le numérateur et le dénominateur pour 5 pour avoir la fraction équivalente 5/10 = 1/2.
2- Diviser par 10 équivaut à multiplier par la puissance basée sur dix avec l'exposant moins un (10 ^ -1), c'est-à-dire 5/10 = 5 × 10 ^ -1.
3- L'exposant négatif indique combien de fois le chiffre indiqué de la position de l'unité est exécuté ou positionné, dans notre cas, il serait de 0,5.
4- ½ = 0,5 en notation étendue, il est écrit comme ceci:
0,5 = 0x10 ^ 0 + 5 × 10 ^ -1
Où 10 ^ -1 = 0,1 est un dixième (la fraction correspondant à l'unité divisée en 10 parties égales).
De cette façon, le nombre de 0,5 correspond à cinq dixièmes, mais le nombre de 0,05 correspond à 5 centièmes et 0,005 à 5 millièmes.
Peut vous servir: pourquoi l'algèbre est-elle importante dans certaines situations de vie quotidiennes?Des exemples de notation développés
Exemple 1
Compte tenu du chiffre 40201 en notation standard, convertissez-le en notation développée.
Solution:
4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1 = 40201
Exemple 2
Écrivez la fraction ¾ en notation prolongée.
Solution:
Dans ce cas, il y a trois trimestres de l'unité.
3/4 = 15/20 = 75/100 = 0,75 = 7/10 + 5/100 =
7 × 10 ^ -1 + 5 × 10 ^ -2.
Dit par des mots serait comme ceci:
La fraction ¾ correspond à sept dixièmes plus cinq centièmes.
Exercices de notation développés
Exercice 1
Disons en mots l'expression développée de la figure 40201 de l'exemple 1.
Solution:
La notation développée est comme ceci:
40201 = 4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1
Que dans la langue des mots, il est dit:
Quatre dizaines de milliers, plus mille mille, plus deux cents cents, plus de dizaines à zéro, plus une unité.
Exercice 2
Exprimer dans les mots la figure précédente et décomposer la phrase correspondante développée.
Solution:
La figure 40201 en mots est exprimée comme suit:
Quarante mille deux cents
La phrase précédente peut se développer comme:
40 × 1000 + 2 × 100 + 1
On peut dire que la façon de prononcer les chiffres est une manière à moitié développée de l'exprimer.
Exercice 3
Écrivez le numéro 7/3 développé.
Solution:
C'est une figure exprimée comme une fraction incorrecte, car comme le numérateur est supérieur au dénominateur, la figure est supérieure à l'unité.
Cette fraction incorrecte peut être décomposée comme la somme des fractions 6/3 + 1/3. La première des fractions se traduit par un nombre entier 2, tandis que 1/3 = 0,333333, où le chiffre 3 est répété indéfiniment. De sorte que l'expression décimale développée de la figure 7/3 sera toujours une expression approximative:
Peut vous servir: quadrilatère: éléments, propriétés, classification, exemples7/3 = 2 + 1/3 ≃ 2 + 0,333 = 2 + 3 × 10 ^ -1 + 3 × 10 ^ -2 + 3 × 10 ^ -3.
Exercice 6
Écrivez en notation standard puis développé le numéro: Vingt-trois milliards de deux cent cinquante millions cinq cent vingt-six mille trois cent vingt-cinq avec trois vingt-trois millièmes.
Solution:
Il faut se rappeler qu'un milliard est l'équivalent d'un milliard. Mot milliard Il a été accepté par la Royal Spanish Academy en 1995 à la demande du défunt président vénézuélien Rafael Caldera, membre de l'Académie vénézuélienne de langue. Dans ce cas, la figure de la notation standard est écrite comme suit:
23.2501526.325 023
23 milliards + 250 millions + 526 mille + 325 unités + 23 millièmes.
23 × 10 ^ 9 + 250 × 10 ^ 6 + 526 × 10 ^ 3 + 325 × 10 ^ 0 + 23 × 10 ^ -3
Enfin, la figure de la notation développée est écrite:
2 × 10 ^ 10 + 3 × 10 ^ 9 + 2 × 10 ^ 8 + 5 × 10 ^ 7 + 0x10 ^ 6 + 5 × 10 ^ 5 + 2 × 10 ^ 4 + 6 × 10 ^ 3 + 3 × 10 ^ 2 + 2 × 10 ^ 1 + 5 × 10 ^ 0 + 0x10 ^ -1 + 2 × 10 ^ -2 + 3 × 10 ^ -3.
Les références
- Académie Khan. Tableaux de valeur de position. Récupéré de: est.Khanacademy.org
- Académie Khan. Écrivez un numéro développé (vidéo). Récupéré de: est.Khanacademy.org
- Ifrah, Geoges (1998): Histoire universelle des figures. Espasa Calpe S.POUR.
- Wikipédia. Notation de position. Récupéré de: est.Wikipédia.com
- Wikipédia. Milliard. Récupéré de: est.Wikipédia.com
- « Structure d'oxyde de phosphore (V), propriétés, objets d'obtention, utilisations, risques
- Structure de phosphate en aluminium (Alpo4), propriétés, obtention, utilisations »

