Nombres transcendants qui sont, des formules, des exemples, des exercices

Les nombres transcendants Ce sont ceux qui ne peuvent pas être obtenus à la suite d'une équation polynomiale. L'opposé d'un nombre transcendant est un numéro algébrique, qui sont des solutions d'une équation polynomiale du type:

pour_n Xⁿ + pour_N-1 X^N-1 +… + A₂ X² + pour₁ x + a₀ = 0

Où les coefficients_n, pour_N-1,… pour₂, pour₁, pour₀ Ce sont des nombres rationnels, appelés coefficients polynomiaux. Si un nombre x est une solution de l'équation précédente, alors ce nombre n'est pas transcendant.

Figure 1. Deux nombres de grande importance en science sont des nombres transcendants. Source: DomainPartures publiques.filet.

Nous analyserons quelques nombres et verrons s'ils sont ou non transcendants:

a) 3 n'est pas transcendant car il s'agit d'une solution de x - 3 = 0.

b) -2 ne peut pas être transcendant car il s'agit d'une solution de x + 2 = 0.

c) ⅓ c'est 3x - 1 = 0 solution

d) une solution de l'équation x² - 2x + 1 = 0 est √2 -1, donc ledit numéro par définition n'est pas transcendant.

e) ni √2 car c'est le résultat de l'équation x² - 2 = 0. En augmentant √2 carré, il en résulte 2, qui soustrait de 2 n'a pas d'importance à zéro. Donc √2 est un nombre irrationnel mais il n'est pas transcendant.

[TOC]

Quels sont les nombres transcendants?

Le problème est qu'il n'y a pas de règle générale pour les obtenir (plus tard nous dirons un formulaire), mais certains des plus célèbres sont le nombre pi et le Nombre de neper, indiqué respectivement par: π et et.

Le nombre π

Le numéro π semble naturellement observer que le quotient mathématique entre le périmètre p d'un cercle et son diamètre d, qu'il s'agisse d'un petit ou grand cercle, donne toujours le même nombre, appelé pi:

π = P / D ≈ 3 14159…

Cela signifie que si le diamètre de la circonférence est pris comme une unité de mesure, pour tous, que ce soit grand ou petit, le périmètre vaudra toujours P = 3,14… = π, comme on peut le voir dans l'animation de la figure 2.

Peut vous servir: théorème de Bolzano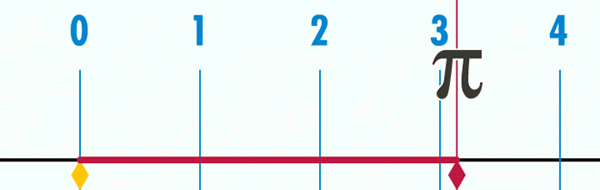Figure 2. La longueur du périmètre d'un cercle est parfois la longueur du diamètre, étant environ 3,1416.

Afin de déterminer plus de décimales, vous devez mesurer plus de précision P et D, puis calculer le quotient, ce qui a été fait de manière mathématique. La conclusion est que les décimales du quotient n'ont aucune fin et ne sont jamais répétées, donc le numéro π En plus d'être transcendant, c'est aussi irrationnel.

Un nombre irrationnel est ce nombre qui ne peut être exprimé comme la division de deux nombres entiers. 

Il est connu que chaque nombre transcendant est irrationnel, mais il n'est pas vrai que tous les irrationnels sont transcendants. Par exemple √2 est irrationnel, mais il n'est pas transcendant.

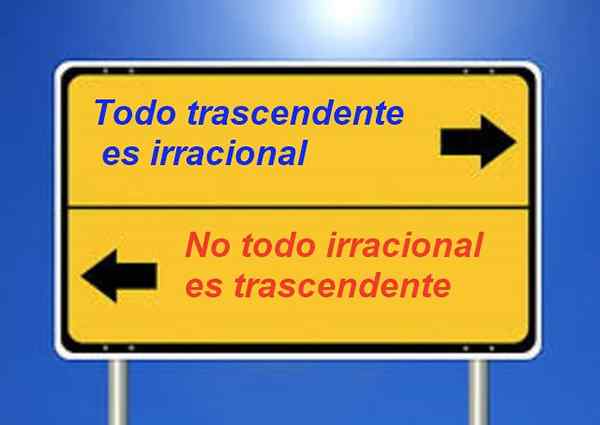figure 3. Les nombres transcendants sont irrationnels, mais la déclaration réciproque n'est pas vraie.

Le numéro E

Le nombre transcendant est la base des logarithmes néépériens et leur approche décimale est:

e ≈ 2.718281828459045235360… .

Si vous vouliez écrire le numéro et Exactement, il serait nécessaire d'écrire décimal infini, car chaque nombre transcendant est irrationnel, comme dit avant.

Les dix premiers chiffres de et Ils sont faciles à retenir:

2.7 1828 1828 Et bien qu'il semble suivre un modèle répétitif, cela n'est pas atteint dans les décimales de l'ordre supérieur à neuf.

Une définition plus formelle de et est la suivante:

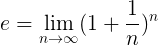
Ce qui signifie que la valeur exacte de et L'opération indiquée dans cette formule est obtenue, lorsque le nombre naturel n Il tend à l'infini.

Cela explique pourquoi nous ne pouvons obtenir que des approches pour et, Étant donné que aussi grand le nombre n est placé, vous pouvez toujours trouver un n âgé.

Cherchons par vous-même certaines approches:

-Quand n = 100 alors (1 + 1/100)¹⁰⁰ = 2 70481 qui coïncide à peine dans la première décimale avec la "vraie" valeur de E.

-Si vous êtes choisi n = 10.000 vous avez (1 + 1/10.000)^dix.000 = 2 71815 qui coïncide avec la valeur «exacte» de E dans les trois premières décimales.

Peut vous servir: côtés homologues

Ce processus doit être suivi pour pouvoir obtenir la "vraie" valeur de E. Je ne pense pas que nous ayons le temps de le réaliser, mais faisons une tentative de plus:

Utilisons n = 100.000:

(1 + 1/100.000)^100.000 = 2,7182682372

Qu'il n'a que quatre décimales coïncidant avec la valeur considérée comme précise.

L'important est de comprendre que plus la valeur de N choisie est grande pour calculer et_n, Plus proche sera de la vraie valeur. Mais cette vraie valeur ne sera maintenue que lorsque n est infini.

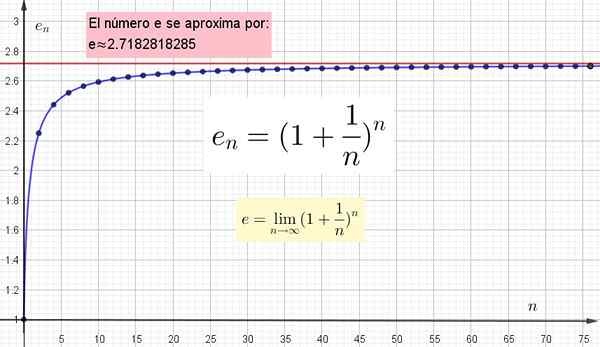Figure 4. Il est représenté graphiquement car la valeur la plus élevée de n est plus proche de E, mais pour atteindre la valeur exacte n doit être infinie.

Autres nombres transcendants

En dehors de ces nombres célèbres, il y a d'autres nombres transcendants, par exemple:

- 2^√2

Tout numéro algébrique, qui n'est pas 0 ou 1, élevé à un exposant irrationnel sera un numéro transcendant.

-Le numéro 10 de Champernowne: 

C_10 = 0,123456789101112131415161718192021… .

-Numéro de Champernowne sur la base 2:

C_2 = 0,110111001011011… .

-Le nombre gamma γ ou constant d'Euler-Mascheroni:

γ ≈ 0,577 215 664 901 532 860 606

Qui est obtenu en effectuant le calcul suivant:

γ ≈ 1 + ½ + ⅓ + ¼ +… + 1 / n - ln (n)

Pour quand n être très grand. Pour avoir la valeur exacte du numéro gamma, il serait nécessaire de calculer avec n infini. Quelque chose de similaire à ce que nous avons fait ci-dessus.

Et il y a beaucoup plus de nombres transcendants. Le grand mathématicien Georg Cantor, né en Russie et a vécu entre 1845 et 1918, a montré que l'ensemble des nombres transcendants est beaucoup plus élevé que l'ensemble des nombres algébriques.

Formules où le nombre transcendant π apparaît

Le périmètre de la circonférence

P = π d = 2 π r, où p est le périmètre, d le diamètre et r le rayon de la circonférence. Il faut se rappeler que:

Peut vous servir: combien devez-vous ajouter à 3/4 pour obtenir 6/7?

-Le diamètre de la circonférence est le segment le plus long qui en rejoint deux points et qui passe toujours par son centre,

-Le rayon est la moitié du diamètre et est le segment qui va du centre au bord.

Zone de cercle

A = π r² = ¼ π d²

Surface d'une sphère

S = 4 π r^2.

Ouais. Bien que cela ne semble pas, la surface d'une sphère est la même que celle de quatre cercles du même rayon que la sphère.

Volume de sphère

V = 4/3 π r³

Exercices

- Exercice 1

La pizzeria "exotique" vend trois pizzas de diamètre: 30 cm Small, médiane 37 cm et grand 45 cm. Un enfant a très faim et s'est rendu compte que deux petites pizzas ont le même coût qu'un grand. Ce qui sera mieux pour lui, achetez deux petites pizzas ou un grand?

Figure 5.- La zone d'une pizza est proportionnelle au carré du rayon, étant la constante de proportionnalité. Source: Pixabay.

Solution

Plus la zone est grande, plus la quantité de pizza est grande, pour cette raison, la zone d'une grande pizza sera calculée et comparée à celle de deux petites pizzas:

Grande pizza = ¼ π d² = ¼ ⋅3,1416⋅45² = 1590,44 cm²

Petite pizza = ¼ π d² = ¼ ⋅3,1416⋅30² = 706,86 cm²

Par conséquent, deux petites pizzas auront une zone de 

2 x 706,86 = 1413,72 cm² .

Il est clair: il y aura plus de pizza acheter un seul grand que deux petites.

- Exercice 2

La pizzeria «exotique» vend également un rayon de 30 cm semi -man-pizza pour la même forme rectangulaire de 30 x 40 cm côté. Lequel choisiriez-vous?

Figure 6.- La surface d'un demi-digne est deux fois la surface circulaire de la base. Source: F. Zapata.

Solution

Comme indiqué dans la section précédente, la surface d'une sphère est quatre fois supérieure à celle d'un cercle du même diamètre, donc un semi -pear de 30 cm de diamètre aura:

30 cm Semi -Man -pizza: 1413.72 cm² (deux fois par circulaire du même diamètre)

Pizza rectangulaire: (30 cm) x (40 cm) = 1200 cm² .

Semi -man -pizza a une plus grande zone.

Les références

1. Fernández J. Le numéro E. Origine et curiosités. Récupéré de: Mathématiques de soja.com
2. Profitez des mathématiques. Numéro d'Euler. Récupéré de: Priematimaticas.com.
3. Figuera, J. 2000. Mathématiques 1er. Diversifié. Éditions co-bo.
4. Garcia, m. Le nombre e dans le calcul élémentaire. Récupéré de: mathématiques.Civils.UCV.aller.
5. Wikipédia. Numéro PI. Récupéré de: Wikipedia.com
6. Wikipédia. Nombres transcendants. Récupéré de: Wikipedia.com