Historique des nombres réels, exemples, propriétés, opérations

Les nombres réels Ils constituent l'ensemble numérique qui englobe les nombres naturels, les entiers, les rationnels et irrationnels. Ils sont indiqués avec le symbole ℝ ou simplement R Et la portée qu'ils ont en science, ingénierie et économie est telle que lorsque vous parlez de "nombre", il est presque supposé que c'est un nombre réel.

Les nombres réels sont utilisés depuis les temps anciens, bien qu'ils n'aient pas reçu ce nom. Depuis le moment où Pythagore a développé son célèbre théorème, des nombres sont nés qui ne pouvaient pas être obtenus comme des nombres plutôt naturels ou des nombres entiers.

Figure 1. Diagramme de Venn montrant comment l'ensemble des nombres réels contient les autres ensembles numériques. Source> Wikimedia Commons.

Des exemples de nombres sont √2, √3 et π. Ces nombres sont appelés irrationnel, Contrairement aux nombres rationnels, qui proviennent de quotients entre les nombres entiers. Il était donc nécessaire un ensemble numérique qui couvre les deux types de nombres.

Le terme «nombre réel» a été créé par le grand mathématicien René Descartes (1596-1650), pour distinguer les deux types de racines qui peuvent résulter de la résolution d'une équation polynomiale.

Certaines de ces racines peuvent être des paires de nombres négatifs, ces descartes les ont appelés "nombres imaginaires" et ceux qui ne l'étaient pas, étaient des nombres réels.

La dénomination a persisté au fil du temps, donnant naissance à deux grands ensembles numériques: nombres réels et nombres complexes, un ensemble plus large qui comprend des nombres réels, imaginaires et ceux qui sont réels et en partie imaginaires.

L'évolution des nombres réels a poursuivi son cours jusqu'en 1872, le mathématicien Richard Dedekind (1831-1936) a défini avec toute la formalité l'ensemble des nombres réels à travers les appels Corrutures Dedekind. La synthèse de son travail a été publiée dans un article qui a vu la lumière la même année.

Peut vous servir: polygones réguliers: propriétés, éléments, angles, exemples

[TOC]

Exemples de nombres réels

Le tableau suivant montre des exemples de nombres réels. Cet ensemble a une sous-ensemble en nombres naturels, entiers, rationnels et irrationnels. Un nombre de ces ensembles est, en soi, un nombre réel.

Par conséquent, les 0, les négatifs, les fractions positives et les décimales sont des nombres réels.

Figure 2. Les exemples de nombres réels sont les indigènes, les entiers, les rationnels, les irrationnels et les transcendants. Source: F. Zapata.

Représentation de nombres réels sur la ligne réelle 

Les nombres réels peuvent être représentés sur la ligne réelle R, Comme le montre l'image. Il n'est pas nécessaire que le 0 soit toujours présent, mais il est pratique de savoir que les Reais négatifs sont à leur gauche et à droite le positif. C'est pourquoi c'est un excellent point de référence.

Sur la ligne réelle, une échelle est prise, dans laquelle les entiers sont trouvés:… 3, -2, -1, 1, 2, 3… . La flèche indique que la ligne s'étend à l'infini. Mais ce n'est pas tout, dans un intervalle considéré, nous trouverons toujours des nombres réels infinis.

Les nombres réels sont représentés dans l'ordre. Pour commencer, il y a l'ordre des nombres entiers, dans lesquels.

Cette commande reste dans les nombres réels. Les inégalités suivantes sont présentées comme exemple:

a) -1/2 < √2

être < π

c) π> -1/2

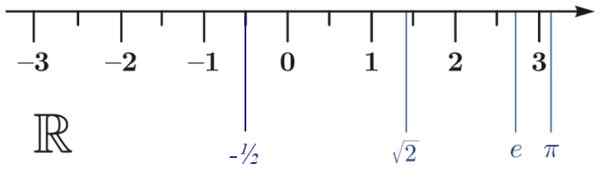figure 3.- La vraie ligne. Source: Wikimedia Commons.

Propriétés des nombres réels

-Les nombres réels incluent des nombres naturels, des entiers, rationnels et irrationnels.

Peut vous servir: quels sont les nombres triangulaires? Propriétés et démonstrations

-La propriété commutative de la somme est remplie: l'ordre des addeds ne modifie pas la somme. Si A et B sont deux vrais nombres, il est toujours vrai que:

A + b = b + a

-0 est l'élément neutre de la somme: a + 0 = a

-La propriété associative est respectée pour la somme. Si a, b et c sont des nombres réels: (a + b) + c = a + (b + c).

-L'opposé d'un réel nombre a est -a.

-La soustraction est définie comme la somme de l'inverse: a - b = a + (-b).

-La propriété commutative du produit est remplie: l'ordre des facteurs ne modifie pas le produit: un.b = b.pour

-La propriété associative est également appliquée au produit: (a.b).C = a.(B.c)

-Le 1 est l'élément neutre de la multiplication: a.1 = A

-La propriété distributive de la multiplication par rapport à l'ajout est valide: un. (b + c) = a.b + a.c

-La division par 0 n'est pas définie.

-Tout numéro réel a, sauf 0, a l'inverse multiplicatif à^-1 tel qu'un.pour^-1 = 1.

-Si A est un nombre réel: A⁰ = 1 et un¹ = A.

-La valeur ou le module absolu d'un nombre réel est la distance entre ledit numéro et 0.

Opérations avec des nombres réels

Avec les nombres réels, vous pouvez effectuer les opérations qui sont faites avec les autres ensembles numériques, y compris la somme, la soustraction, la multiplication, la division, l'amélioration, le rayonnement, les logarithmes et plus.

Comme toujours, la division de 0 n'est pas définie, il n'y a pas non plus de logarithmes de nombres négatifs ou 0, bien qu'il soit vrai que le log 1 = 0 et que les logarithmes de nombres entre 0 et 1 sont négatifs.

Applications

Les applications de nombres réels à toutes sortes de situations sont extrêmement variés. Les nombres réels apparaissent en réponse à de nombreux problèmes en sciences exactes, en informatique, en ingénierie, en économie et en sciences sociales.

Il peut vous servir: Hipparco de Nicea: biographie et contributions à la science

Toutes sortes de grandeur et de montants telles que les distances, les temps, les forces, l'intensité sonore, l'argent et bien d'autres, ont leur expression en nombre réel.

La transmission des signaux téléphoniques, l'image et le son d'une vidéo, la température d'une climatisation, un radiateur ou un réfrigérateur peuvent être contrôlés numériquement, ce qui signifie transformer les amplitudes physiques en séquences numériques.

La même chose se produit lorsqu'une transaction bancaire est effectuée en ligne ou que la messagerie instantanée est consultée. Les vrais nombres sont partout.

Exercice résolu

Voyons avec des exercices comment ces chiffres fonctionnent dans des situations communes avec lesquelles nous sommes quotidiennement.

Exercice 1

Le bureau de poste n'accepte que des forfaits pour lesquels la longueur, plus la mesure du contour, ne dépasse pas 108 pouces. Par conséquent, pour que le package soit accepté, il doit être réalisé que:

L + 2 (x + y) ≤ 108

a) passerez-vous un paquet qui mesure 6 pouces de large, 8 pouces de hauteur et 5 pieds de long?

b) Qu'en est-il de celui qui mesure 2 x 2 x 4 pieds³?

c) Quel est le plus élevé acceptable pour un paquet dont la base est carrée et mesure 9 x 9 pouces²?

Réponds à

L = 5 pieds = 60 pouces

x = 6 pouces

y = 8 pouces

L'opération à résoudre est:

L + 2 (x + y) = 60 + 2 (6 + 8) pouces = 60 + 2 x 14 pouces = 60 + 28 pouces = 88 pouces

Le package est accepté.

Réponse b

Les dimensions de ce paquet sont inférieures à celles de l'emballage A), donc les deux parviennent à passer.

Réponse C

Dans ce package:

x = l = 9 pouces

Il faut accomplir que:

9+ 2 (9+ y) ≤ 108

27 + 2y ≤ 108

2Y ≤ 81

et ≤ 40.5 pouces

Les références

1. Carena, m. 2019. Manuel des mathématiques de préunité. Université nationale de la côte.
2. Diego, un. Les nombres réels et leurs propriétés. Récupéré de: mathématiques.Non.Édu.ardente.
3. Figuera, J. 2000. Mathématiques 9e. degré. Éditions co-bo.
4. Jiménez, R. 2008. Algèbre. Prentice Hall.
5. Stewart, J. 2006. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.