Angles supplémentaires qui sont, calcul, exemples, exercices

Deux ou plus sont angles supplémentaires Si la somme de ses mesures correspond à la mesure d'un angle plat. La mesure d'un angle plat, également appelé angle plat, en degrés est de 180 ° et en rayons est π.

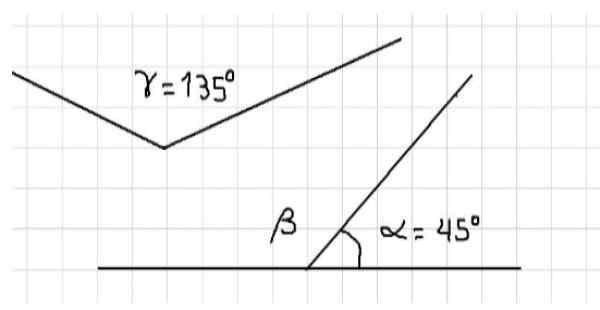
Par exemple, nous constatons que les trois angles intérieurs d'un triangle sont supplémentaires, car la somme de ses mesures est de 180 °. Trois angles sont illustrés à la figure 1. De ce qui précède, il s'ensuit que α et β sont supplémentaires, car ils sont adjacents et leur somme pleine un angle plat.

Figure 1: α et β sont supplémentaires. α et γ sont supplémentaires. Source: F. Zapata.

Également dans cette même figure, il y a des angles α et γ qui sont également supplémentaires, car la somme de leurs mesures est égale à l'étendue d'un angle plat, c'est-à-dire à 180º. On ne peut pas dire que les angles β et γ sont supplémentaires car les deux angles obtus, leurs mesures sont supérieurs à 90 ° et donc sa somme dépasse 180º.

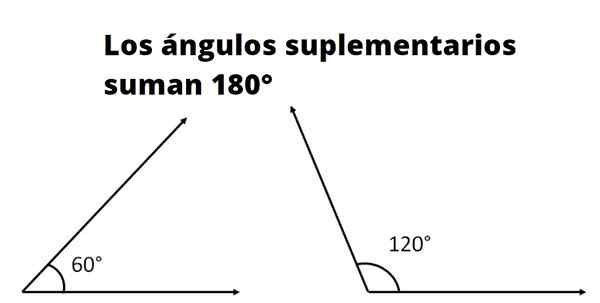Source: Lafer.com

D'un autre côté, on peut dire que la mesure de l'angle β est égale à la mesure de l'angle γ, car si β est supplémentaire de α et γ est supplémentaire de α, alors β = γ = 135º.

[TOC]

Exemples

Dans les exemples suivants, il est demandé de trouver les angles inconnus, indiqués par l'interrogatoire de la figure 2. Ils vont des exemples les plus simples à certains un peu plus élaborés que le lecteur ne devrait être plus prudent.

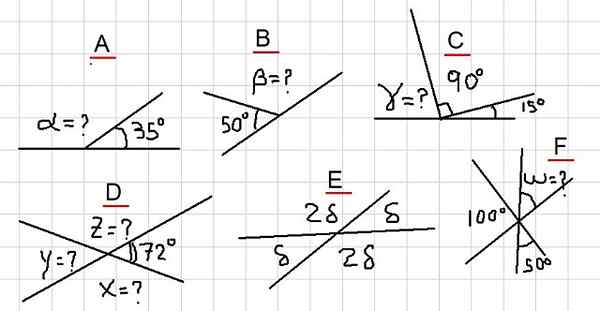Figure 2. Divers exemples d'angles supplémentaires. Source: F. Zapata.

Exemple A

Dans la figure, nous avons que les angles adjacents α et 35º ajoutent un angle plat. C'est-à-dire α + 35º = 180º et donc il est accompli que: α = 180º-- 35º = 145º.

Exemple B

Comme β est supplémentaire avec l'angle de 50º, il est suivi que β = 180º - 50º = 130º.

Peut vous servir: quels sont les éléments de la parabole? (Les pièces)

Exemple C

À partir de la figure 2c, la somme suivante est remarquée: γ + 90º + 15º = 180º. C'est-à-dire que γ est supplémentaire avec l'angle 105º = 90º + 15º. Il est alors conclu que: 

γ = 180º- 105º = 75º

Exemple D

Comme x est supplémentaire avec 72º, il s'ensuit que x = 180º - 72º = 108º. De plus et il est supplémentaire avec x, alors y = 180º - 108º = 72º.

Et enfin z est supplémentaire avec 72º, donc z = 180º - 72º = 108º.

Exemple E

Les angles Δ et 2δ sont supplémentaires, donc Δ + 2Δ = 180º. Ce qui signifie que 3Δ = 180º, et cela permet à son tour l'écriture: δ = 180º / 3 = 60º.

Exemple F

Si nous appelons l'angle entre le 100 ° et le 50º, il est alors nécessaire de leur être complété, car il est observé que leur somme pleine un angle plat.

Il s'ensuit que u = 150º. Comme u est opposé par le sommet à w, alors w = u = 150º.

Exercices

Trois exercices sont proposés ci-dessous, dans chacun d'eux, la valeur des angles A et B doit être trouvée en degrés, de sorte que les relations illustrées à la figure 3 sont satisfaites. Le concept d'angles supplémentaires est utilisé dans la résolution de tous.

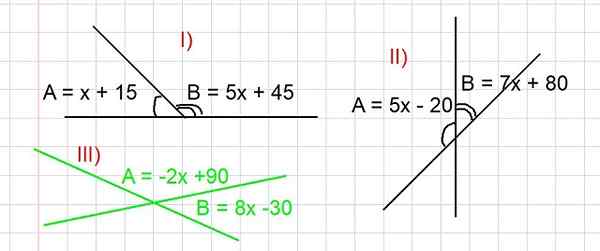figure 3. Figure pour résoudre les exercices I, II et III sur des angles supplémentaires. Tous les angles sont exprimés en degrés. Source: F. Zapata.

- Exercice I

Déterminez les valeurs des angles a et b de la partie I) de la figure 3.

Solution

A et B sont supplémentaires, où A + B = 180 degrés doivent être remplacés, alors l'expression de A et B est remplacée en fonction de x, comme il apparaît dans l'image:

(x + 15) + (5x + 45) = 180

Une équation linéaire de premier ordre est obtenue. Pour le résoudre, les termes sont jetés: les termes:

6 x + 60 = 180

Peut vous servir: Nombres réels: historique, exemples, propriétés, opérations

Les deux membres entre 6 sont:

x + 10 = 30

Et enfin la compensation, il s'ensuit que X vaut 20º.

Maintenant, la valeur de x doit être remplacée pour trouver les angles commandés. De là, vous devez l'angle a est: a = 20 +15 = 35º.

Et pour sa part, l'angle b est b = 5 * 20 + 45 = 145º.

- Exercice II

Trouvez les valeurs des angles A et B de la partie II) de la figure 3.

Solution

Comme a et b sont des angles supplémentaires, A + B = 180 degrés ont. Le remplacement de l'expression de A et B en fonction de x donnée dans la partie II) de la figure 3 est:

(-2x + 90) + (8x - 30) = 180

Encore une fois, une équation au premier degré est obtenue, pour laquelle les termes doivent être commodément en groupe:

6 x + 60 = 180

Les deux membres entre 6 sont:

x + 10 = 30

Où il suit que x vaut 20º.

C'est-à-dire que l'angle a = -2 * 20 + 90 = 50 °. Tandis que l'angle b = 8 * 20-30 = 130.

- Exercice III

Déterminez les valeurs des angles A et B de la partie III) de la figure 3 (en vert).

Solution

Comme a et b sont des angles supplémentaires, A + B = 180 degrés ont. L'expression de A et B doit être remplacée en fonction de X donnée dans la figure 3, que vous avez:

(5x - 20) + (7x + 80) = 180

12 x + 60 = 180

Divisant les deux membres par 12 pour effacer la valeur de x, vous avez:

x + 5 = 15

Enfin, on constate que X vaut 10 degrés.

Continuez maintenant à remplacer pour trouver l'angle A: A = 5 * 10 -20 = 30 °. Et pour l'angle b: b = 7 * 10 + 80 = 150º

Peut vous servir: quelle est la gamme de statistiques? (Avec des exemples)

Angles supplémentaires en deux parallèles coupés par un sécant

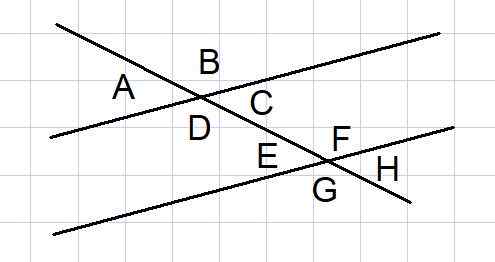Figure 4. Angles entre deux parallèles coupés par un sécant. Source: F. Zapata.

Deux lignes parallèles coupées par une sécante est une construction géométrique habituelle dans certains problèmes. Parmi ces lignes, 8 angles sont formés comme le montre la figure 4.

De ces 8 angles, certaines paires d'angles sont supplémentaires, que nous énumèrent ci-dessous:

1. Les angles externes à et b, et les extérieurs g et h
2. Les angles intérieurs d et c, et les intérieurs e et f
3. Les angles externes A et G, et les B et H externes
4. Les angles internes D et E, et les détenus C et F

Par exhaustivité, les angles égaux sont également nommés:

1. Les alternations internes: d = f et c = e
2. Les alternances externes: a = h et b = g
3. Les correspondants: a = e et c = h
4. Les opposés par sommet a = c et e = h
5. Les correspondants: b = f et d = g
6. Les opposés par sommet b = d et f = g

- Exercice IV

En référence à la figure 4, dans laquelle les angles montrent entre deux lignes parallèles coupées par une sécante, déterminez la valeur de tous les angles dans les radians, sachant que l'angle a = π / 6 radians.

Solution

A et b sont des angles externes supplémentaires donc b = π - a = π - π / 6 = 5π / 6

A = e = c = h = π / 6

B = f = d = g = 5π / 6

Les références

1. Baldor, J. POUR. 1973.Géométrie plate et espace. Culturel d'Amérique centrale. 
2. Lois et formules mathématiques. Systèmes de mesure d'angle. Récupéré de: Ingecanica.com.
3. Wentworth, G. Géométrie de la planète. Récupéré de: Gutenberg.org.
4. Wikipédia. Angles supplémentaires. Récupéré de: est.Wikipédia.com
5. Wikipédia. Convoyeur. Récupéré de: est.Wikipédia.com
6. Zapata f. Goniomètre: historique, pièces, opération. Récupéré de:.com