Angles dans les types de circonférence, propriétés, exercices résolus

Ils s'appellent Angles de circonférence à ceux dans lesquels l'un de ses éléments est ou se croise à une circonférence donnée. Parmi eux se trouvent les suivants:

1.- Il angle central, dont le sommet se trouve au centre de la circonférence et ses côtés se séchent, comme nous le voyons dans l'image suivante:

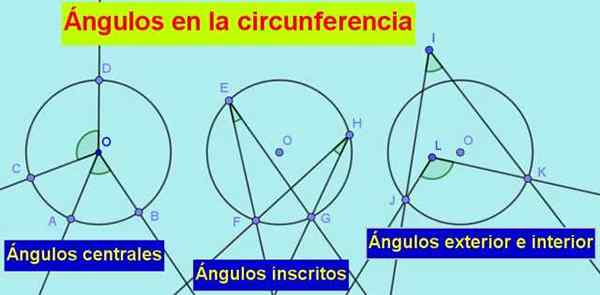
Figure 1. Les types d'angles dans la circonférence sont: le centre, l'inscription, l'extérieur et l'intérieur. Source: F. Zapata.

2.- Il angle enregistré, dont le sommet est sur la circonférence et ses côtés sont secs ou tangents à la circonférence.

3.- Angle extérieur, dont le sommet est hors de la circonférence mais ses côtés sont secs ou tangents à la circonférence.

4.- Il Angle intérieur, avec le sommet à l'intérieur de la circonférence et de ses côtés secs.

Tous ces angles maintiennent certaines relations les uns avec les autres et cela nous amène à des propriétés importantes entre les angles appartenant à une circonférence donnée.

[TOC]

Propriétés

- Angle central

L'angle central est défini comme celui dont le sommet est au centre de la circonférence et ses côtés coupés dans la circonférence.

La mesure des rayons d'un angle central est le quotient entre l'arc qui sous-tend, c'est-à-dire l'arc de circonférence entre les côtés de l'angle et le rayon de la circonférence. 

Si la circonférence est unitaire, c'est-à-dire le rayon 1, alors la mesure de l'angle central est la longueur de l'arc, qui correspond au nombre de radians.

Si vous voulez la mesure de l'angle central en degrés, alors la mesure est multipliée en radians par le facteur 180º / π.

Les instruments de mesure des angles, tels que le transporteur et le goniomètre, utilisent toujours un angle central et la longueur de l'arc sous-tendance.

Peut vous servir: Dérivés partiels: propriétés, calcul, exercices

Ils sont calibrés dans des degrés Sexagesimal, ce qui signifie que chaque fois qu'un angle est mesuré avec eux, à l'arrière, ce qui est mesuré est la longueur de l'arc sous-tendu par l'angle central.

Propriété

La mesure d'un angle central dans les rayons est égale à la longueur de l'arc qui sous-tit ou intercepte divisé par la longueur du rayon.

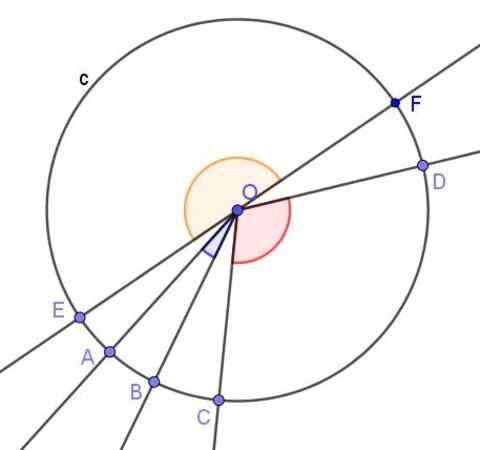Figure 2. Trois angles centraux sont affichés. Un aigu, l'autre obtus et un plat. Source: F. Zapata.

- Angle enregistré

L'angle enregistré d'une circonférence est celui qui a son sommet sur la circonférence et son semi-sort est sec ou tangent au même. 

Ses propriétés sont:

Propriétés

-L'angle enregistré est convexe ou plat.

-Lorsqu'un angle inscrit intercepte le même arc que l'angle central, la mesure du premier sera la moitié de celle du second.

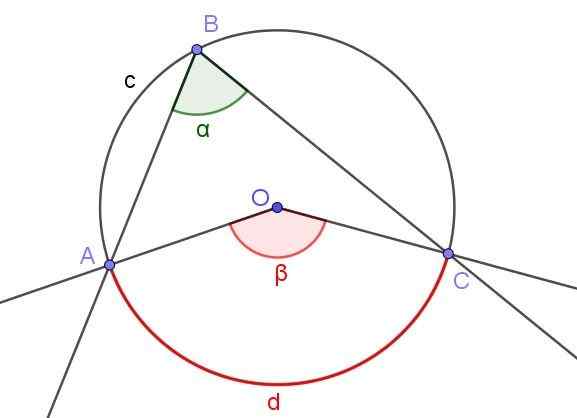figure 3. Angle enregistré ∠ABC et angle central ∠aoc qui sous-tirite le même arc a⌒c. Source: F. Zapata.

La figure 3 montre deux angles ∠ABC et ∠AOC qui interceptent le même arc de circonférence a⌒c.

Si la mesure de l'angle enregistré est α, alors la mesure β de l'angle central est le double de la mesure de l'angle enregistré (β = 2 α) car les deux soustraient le même arc mesuré D.

- Angle extérieur

C'est l'angle dont le sommet est en dehors de la circonférence et chacun de ses côtés coupe à la circonférence en un ou plusieurs points.

Propriété

-Sa mesure est égale à la semi-expression (ou à la différence divisée par 2) des angles centraux qui interceptent les arches elles-mêmes.

Pour s'assurer que la mesure est positive, la semi-exprimée doit toujours être l'angle central de la plus grande mesure moins la mesure de l'angle central inférieur, comme illustré sur la figure suivante.

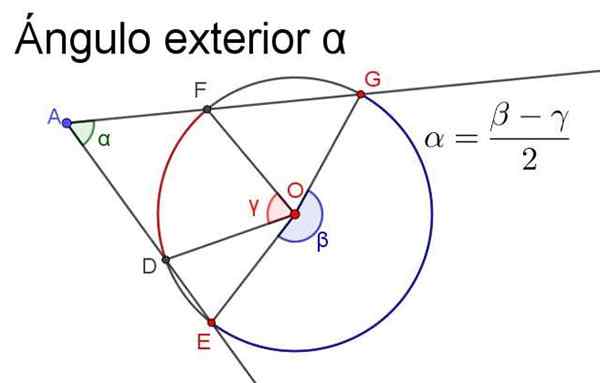Figure 4. L'angle externe α est égal à la semi-référence des centrales qui sous -dent les mêmes arches. Source: F. Zapata.

- Angle intérieur

L'angle intérieur est celui dont le sommet est à l'intérieur de la circonférence et ses côtés coupés à la circonférence.

Peut vous servir: coefficient de détermination: formules, calcul, interprétation, exemples

Propriété 

Sa mesure est égale au semi-groupe de l'angle central qui sous-tend le même arc, plus l'angle central qui sous-tend le même arc que son angle d'extension (c'est l'angle intérieur formé par le semi -té complémentaire à ceux de l'original angle intérieur).

La figure suivante illustre et clarifie la propriété de l'angle intérieur.

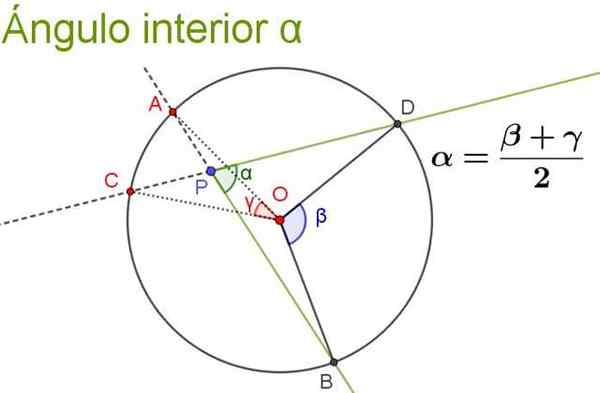Figure 5. L'angle intérieur α est égal au semi-seismum des angles centraux qui sous -dent les mêmes arches que lui-même. Source: F. Zapata.

Exercices résolus

- Exercice 1

Supposons un angle inscrit dans lequel l'un de ses côtés passe à travers le centre de la circonférence, comme le montre la figure 6. Le rayon de la circonférence est OA = 3 cm et l'arc d a une longueur de π / 2 cm. Déterminer la valeur des angles α et β.

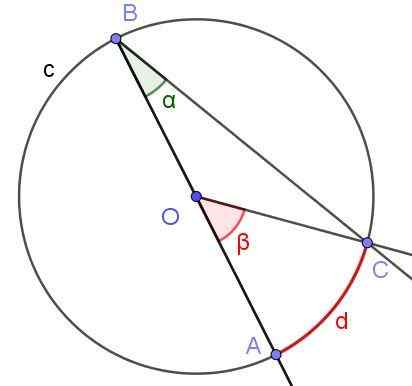Figure 6. Angle enregistré ∠ABC avec le côté [BA) à travers O et Angle central ∠AOC.Source: F. Zapata.

Solution

Dans ce cas, le triangon isocèle COB est formé, puisque [OC] = [OB]. Dans un triangle isocèle, les angles adjacents à la base sont les mêmes, ils doivent donc ∠bco = ∠abc = α. En revanche ∠cob = 180º - β. Compte tenu de la somme des angles internes du triangle COB que vous avez:

α + α + (180º - β) = 180º

D'où il s'ensuit que 2 α = β, ou ce qui est équivalent α = β / 2, qui confirme la propriété (3) de la section précédente, que la mesure de l'angle enregistré est la moitié de l'angle central, lorsque les deux angles soustraient la même corde [ac].

Maintenant, nous continuons à déterminer les valeurs numériques: l'angle β est central et sa mesure dans les rayons est le rapport entre l'arc d et le rayon r = OA, donc sa mesure est:

β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30º.

Peut vous servir: quadrilatère: éléments, propriétés, classification, exemples

En revanche, il avait déjà été affirmé que α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º. 

- Exercice 2

Dans la figure 7, les angles α₁ et β₂ avoir la même mesure. De plus, l'angle β₁ Il mesure 60º. Déterminer les angles β et α.

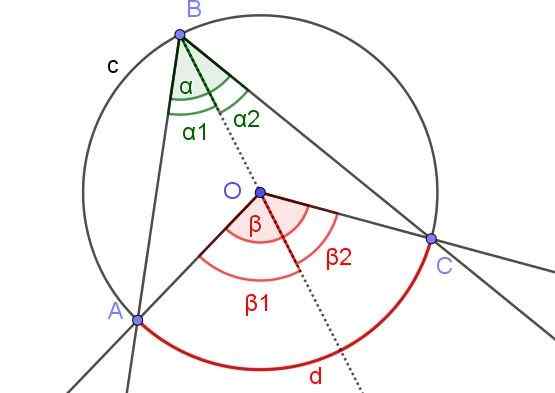Figure 7. Dans la figure α₁ = β₂ et β₁ = 60º. Déterminer les valeurs de β et α. Source: F. Zapata.

Solution

Dans ce cas, il y a un angle inscrit ∠ABC dans lequel le centre ou la circonférence est à l'intérieur de l'angle.

En raison de la propriété (3) vous avez α₂ = β₂ / 2 et α₁ = β₁ / 2. Comme:

α = α₁ + α₂ et β = β₁ + β₂

Vous avez donc:

α = α₁ + α₂ = β₁ / 2 + β₂ / 2 = (β₁ + β₂) / 2 = β / 2.

C'est-à-dire selon les propriétés:

α = β / 2

Comme on nous dit que β₁ = 60º alors:

α₁ = β₁ / 2 = 60º / 2 = 30º.

Ils nous disent aussi que α₁ = β₂ Il s'ensuit donc que:

β₂ = 30º.

L'angle β est:

β₁ + β₂ = 60º + 30º = 90º.

Et comme α = β / 2, alors:

α = 90º / 2 = 45º. 

En conclusion:

β = 90º et α = 45º.

Les références

1. Baldor, un. 1973. Géométrie et trigonométrie. Éditorial culturel d'Amérique centrale.
2. ET. POUR. 2003. Éléments de géométrie: avec des exercices et une géométrie de la boussole. Université de Medellin.
3. Géométrie 1ère. Angles dans la circonférence. Récupéré de: edu.Xunta.est.
4. Toute science. Exercices résolus d'angles dans la circonférence. Récupéré de: Francesphysics.Blogspot.com
5. Wikipédia. Angle enregistré. Récupéré de: est.Wikipédia.com