Explication de la condition du deuxième équilibre, exemples, exercices

La Deuxième condition d'équilibre Il établit que la somme des couples ou des moments produits par toutes les forces qui agissent sur un corps, quel que soit le point calculé, doit être annulé afin que ledit corps soit en équilibre statique ou dynamique.

Indiquant le couple ou le moment de force à travers la lettre grecque τ, Mathématiquement, il est exprimé comme suit:

∑ τ = 0

Figure 1. Pour équilibrer le rocker, il est nécessaire d'appliquer la deuxième condition d'équilibre. Source: pxhere.

La lettre audacieuse indique la nature vectorielle du moment, qui doit être annulée par rapport à tout point choisi comme centre de spin. De cette façon, annulant le couple net, il est garanti que l'objet ne commence pas à tourner ou à tourner.

Cependant, si l'objet tournait déjà auparavant et que le couple net disparaît soudainement, la rotation se poursuivra, mais avec une rapidité angulaire constante.

La deuxième condition d'équilibre est utilisée en conjonction avec la première condition, qui dit que la somme des forces sur un corps doit être vide, de sorte qu'elle ne bouge pas, ou que si elle le fait, c'est avec un mouvement rectiligne uniforme:

∑ F = 0

Les deux conditions s'appliquent aux corps étendus, ceux dont les dimensions sont mesurables. Lorsqu'un objet est censé être une particule, cela n'a aucun sens de parler des rotations, et la première condition pour garantir l'équilibre est suffisant.

Exemples

La deuxième condition d'équilibre est révélée dans d'innombrables situations:

Lorsque vous montez les escaliers

Lorsque vous soutenez un escalier sur le sol et le mur, nous avons besoin de suffisamment de frottement, en particulier sur le sol, pour nous assurer que l'escalier ne glisse pas. Si nous essayons de grimper sur une échelle soutenue sur un sol huileux, humide ou glissant, il n'est pas difficile d'anticiper que nous tomberons.

Pour pouvoir utiliser l'escalier en toute confiance, il est nécessaire qu'il soit en équilibre statique pendant l'escalade et lorsqu'il est dans l'étape nécessaire.

Il peut vous servir: Pluton (planète naine)

Déplacer un placard

Lorsque vous souhaitez déplacer un meuble élevé en tant que placard, ou toute pièce dont le haut est supérieur à son large, il est pratique de pousser sur un point bas, pour éviter le renversement, de cette façon, il est plus probable que le mobilier glissera à la place à la place de tourner et de se coucher.

Dans de telles circonstances, le mobilier n'est pas nécessairement en équilibre, car il pourrait être déplacé rapidement, mais au moins il ne tournerait pas.

Balcons

Les balcons qui excellent les bâtiments doivent être construits garantissant que, bien qu'il y ait beaucoup de gens sur le dessus, il ne tourne pas et ne s'effondre pas.

Diélectrique dans les champs électriques externes

Lorsque vous placez un matériau diélectrique dans un champ électrique externe, les molécules se déplacent et tournent pour adopter une position d'équilibre, créant un champ électrique à l'intérieur du matériau.

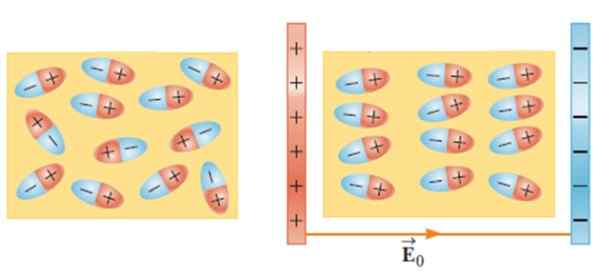Figure 2.- Sans champ électrique externe, les dipôles sont randomisés (à gauche). Le champ externe applique un couple sur les molécules diélectriques et celles-ci sont réorganisées. Source: Serow, R. Physique pour la science et l'ingénierie.

Cet effet fait augmenter la capacité d'un condenseur lorsqu'un matériau tel que le verre, le caoutchouc, le papier ou l'huile est introduit entre son armure.

Signes et lampes

Il est courant pour de nombreux locaux de suspendre des avis sur le mur du bâtiment, afin qu'ils soient visibles pour les passants.

L'affiche est fixée par une barre et un câble, tous deux fixés sur le mur en utilisant des supports. Les différentes forces qui agissent doivent garantir que l'affiche ne tombe pas, pour laquelle les deux conditions d'équilibre entrent en action.

Un réflecteur dans un parc peut également être placé de cette manière, comme dans la figure suivante:

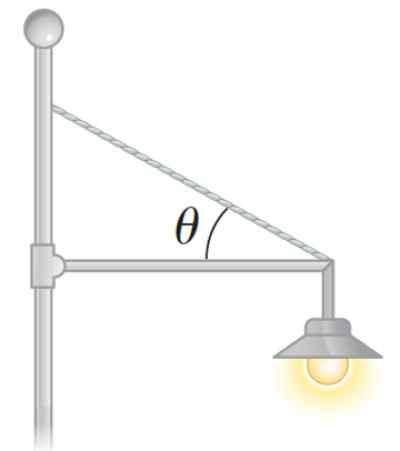figure 3. Une lampe d'équilibre statique. Source: SERRAY. Physique pour la science et l'ingénierie.

Comment calculer le couple net ou le moment net d'une force?

Le couple ou le moment de force, indiqué par τ soit M Dans certains textes, il est toujours calculé par rapport à un moment où l'axe de rotation passe.

Il est défini comme le produit vectoriel entre le vecteur de position r, qui est dirigé dudit axe au point d'application de la force et de la force F:

Peut vous servir: équilibre thermodynamique: classes et applications

τ = r × F

Étant un vecteur, il est nécessaire d'exprimer le couple donnant son ampleur, sa direction et son sens. L'ampleur est donnée par:

τ = RF.sin θ

Règle de droite pour le produit vectoriel

Lorsque le problème est dans le plan, l'adresse de couple est perpendiculaire au papier ou à l'écran et que la direction est déterminée par la règle de droite, dans laquelle l'index pointe vers r, Le majeur vers F Et les signaux du pouce dans ou hors papier.

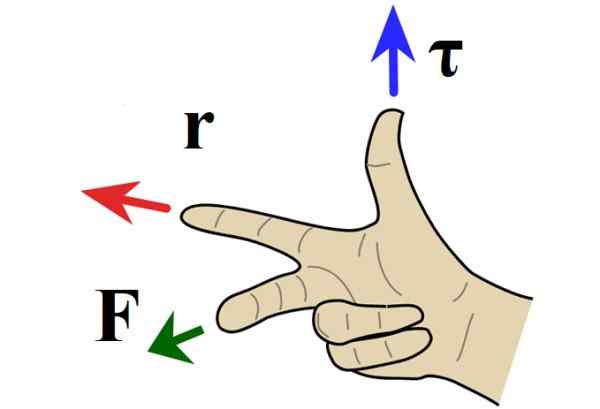Figure 4. Règle de droite pour le produit vectoriel. Source: Wikimedia Commons.

Lorsque le couple pointe du papier, la rotation est dans la direction opposée aux aiguilles de l'horloge et se voit attribuer un signe positif par convention. Si au lieu de cela le couple est dirigé dans la feuille, la rotation est dans la direction des mains et du signe négatif.

Pour trouver le couple net, un point pratique pour le calcul est choisi, qui peut être celui dans lequel la plus grande quantité de forces agit. Dans ce cas, le moment de ces forces est vide, pour avoir un vecteur de position r de magnitude 0.

Vous pouvez choisir n'importe quel point qui offre suffisamment d'informations pour effacer l'inconnu qui demande que le problème soit résolu. Voyons-le plus en détail alors.

Exercice résolu

Le réflecteur de la figure suivante a 20 kg de masse et est soutenu par une barre mince horizontale, de masse et de longueur méprisable L, qui est articulée à un post. Le câble, également léger, qui aide à maintenir le réflecteur forme un angle θ = 30 º avec la barre. Calculer:

a) La tension dans le câble

b) l'ampleur de la force f que le poteau exerce sur la barre à travers la charnière.

Solution

Nous appliquerons la première condition d'équilibre ∑ F = 0 aux forces montrées dans le diagramme:

Peut vous servir: chaleur absorbée: formules, comment la calculer et résoudre des exercices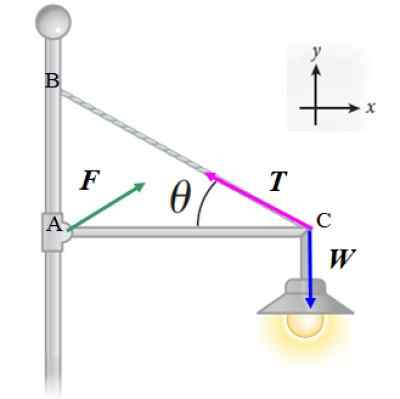

F + T + W = 0

Notez que l'ampleur et la direction de F Ils ne sont pas encore déterminés, mais nous supposons qu'il a deux composantes: F_X et f_et. De cette façon, nous obtenons deux équations:

F_X -T. cos θ = 0

F_et - W + t⋅ sin θ = 0

Maintenant, appliquons la deuxième condition d'équilibre, en choisissant le point A, car nous ne connaissons pas l'ampleur de F ni ce de T. Lors du choix de ce point, le vecteur r_POUR est vide, donc le moment de F est vide et l'ampleur de F Il n'apparaîtra pas dans l'équation:

-W⋅l + t⋅sen θ⋅l = 0

Donc:

T.sin θ.L = w.L

T = w / sen θ = (20 kg x 9.8 m / s²) / Sin 30 º = 392 n

Connaissant l'ampleur de T, nous pouvons effacer le composant F_X:

F_X = T⋅ cos θ = 392 cos 30º n = 339. 5 N

Puis composant f_et:

F_et = W - t⋅ sin θ = (20 kg x 9.8 m / s²) - 392⋅sen 30 º = 0

Ensuite, nous pouvons exprimer F Donc:

F = 339.5 N X

C'est donc une force horizontale. C'est parce que nous considérons que la barre avait un poids méprisable.

Si le point C avait été choisi pour calculer le moment résultant, les vecteurs r_T et r_W Ils sont donc nuls:

M = f_Y⋅L = 0

Il est conclu que f_et = 0. De cette façon:

- W + t⋅ sin θ = 0

T = w / sin θ

Qui est le même résultat initialement obtenu en choisissant le point A comme site où l'axe de rotation passe.

Thèmes d'intérêt

Conditions d'équilibre.

Première condition d'équilibre.

Les références

1. Bedford, 2000. POUR. Mécanique pour l'ingénierie: statique. Addison Wesley.
2. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 4. Systèmes de particules. Édité par Douglas Figueroa (USB).
3. Giancoli, D.  2006. Physique: principes avec applications. 6e. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1.
5. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7e. Élégant. Cengage Learning.