Multiplication des fractions comment elle se fait, exemples, exercices

La Multiplication des fractions C'est une opération arithmétique entre deux ou plusieurs fractions qui donnent naissance à une nouvelle fraction. Son numérateur multiplie les numérateurs des fractions participantes, et le dénominateur est de la même manière.

Voyons-le avec un exemple dans l'image suivante. Supposons qu'il y ait deux fractions A / B et C / D, avec B et D différent de 0.

Figure 1. La multiplication des fractions est une opération qui est effectuée en ligne. Source: F. Zapata.

Pour effectuer la multiplication entre eux, le produit est fabriqué entre les numérateurs et aussi celui des dénominateurs. De cette façon, une nouvelle fraction est créée où le numérateur et le dénominateur sont respectivement: (a × c) et (b × d).

Cette procédure est facilement étendue à la multiplication de trois fractions et plus. Voyons plus de détails ci-dessous.

Comment la multiplication des fractions est-elle effectuée?

Le produit peut être symbolisé par une croix ou avec un point entrecoupé entre les fractions. En outre, il faut tenir compte du fait que les fractions peuvent avoir un signe positif ou un signe négatif, il est donc nécessaire de faire attention à suivre la règle des signes:

-Lorsque deux nombres de signes égaux sont multipliés, le produit est positif.

-Si deux quantités de signes différents sont multipliées, le résultat est négatif.

De cette manière:

Une fois la procédure effectuée, la fraction est simplifiée, si possible. Ceci dans le cas où le numérateur et le dénominateur ne sont pas des cousins ​​les uns avec les autres. Par exemple:

Si le numérateur et le dénominateur des fractions participants ne sont pas des cousins ​​les uns avec les autres, il est pratique de les simplifier avant de faire la multiplication des fractions. De cette façon, des nombres plus petits et plus gérables sont obtenus lors de l'exécution des produits.

Peut vous servir: combien de solutions une équation quadratique a-t-elle?

Propriétés de la multiplication des fractions

Produit par 0

Toute fraction multipliée par 0 est égale à 0:

Produit par 1

Toute fraction multipliée par 1 est égale à elle-même:

Par conséquent, le 1 est considéré élément neutre de multiplication. Notez que l'intégralité du numéro 1 a une expression fractionnée:

De telle manière que nous pouvons nous multiplier à 1 par n'importe quelle fraction, au moyen de la règle déjà expliquée. Donc:

Propriété commutative

La multiplication des fractions est commutative, ce qui signifie que l'ordre des facteurs ne modifie pas le produit:

Propriété associative

La multiplication des fractions est également associative, nous pouvons vérifier en multipliant trois fractions:

Où, comme toujours, les dénominateurs B, D et F sont différents de 0.

En mots: si nous voulons multiplier trois fractions, nous pouvons choisir de fabriquer le produit des deux premiers et de multiplier le résultat par la troisième fraction. Ou multiplier les deux derniers et leur résultat le multiplier enfin par la première des fractions.

Quelle que soit l'ordre choisi, le résultat sera le même. Vérifions-le:

Pour effectuer l'opération, les deux premières fractions ont été multipliées de gauche à droite. Le résultat a été multiplié à son tour par la troisième fraction pour obtenir le résultat final.

L'autre alternative est de multiplier les deux dernières fractions, laissant la première attente. Le lecteur peut voir que le résultat intermédiaire se compose de deux fractions différentes de celles obtenues dans l'autre sens. Mais le résultat final est le même:

Propriété distributive concernant la somme

Laissez trois fractions A / B, C / D et E / F, avec B, D et F différent de 0. La multiplication est distributive en ce qui concerne la somme.

Supposons que nous voulons effectuer l'opération suivante:

La façon de le réaliser, à travers cette propriété, est la suivante:

Il peut vous servir: Test de Tukey: qu'est-ce que, en cas d'exemple, un exercice résolu

Par conséquent, le produit d'un nombre pour la somme de deux autres peut être fait en ajoutant deux produits: le premier pour le deuxième et le premier par le troisième. C'est très simple par un exemple:

Le résultat final semble simplifié au maximum, comme expliqué ci-dessus.

Exemples

Multiplication d'une fraction par un entier

Supposons que vous souhaitiez multiplier une fraction A / B par un entier n:

Nous avons déjà vu que le numéro 1 peut être exprimé comme une fraction, en plaçant simplement comme un dénominateur à 1. Nous pouvons faire de même avec n'importe quel entier n, car le diviser par 1 ne le modifie pas du tout. Ensuite:

Par exemple:

Exemple 2: Multiplication d'une fraction par un nombre mixte

Un nombre mixte ou une fraction mixte, est une partie entière et une partie fractionnaire. Pour effectuer le produit d'un tel nombre, soit avec une fraction, un autre nombre mixte ou avec un entier, il est nécessaire de le transformer à son tour en fraction.

La fraction qui représente un nombre mixte est un Fraction impropre, A dont le numérateur a une valeur absolue plus grande que le dénominateur.

Nous pouvons l'obtenir par la somme de la partie entière, commodément exprimée en fraction en plaçant un 1 en tant que dénominateur, plus la partie fractionnée.

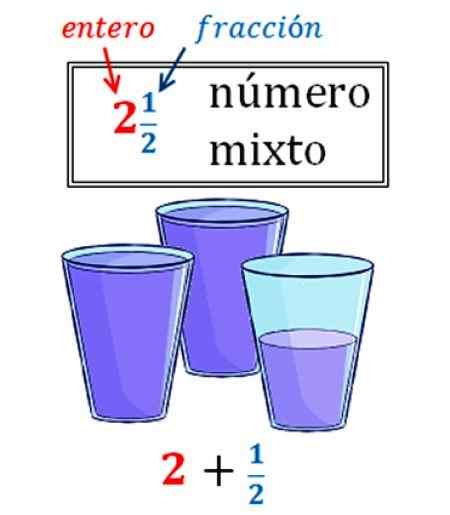Figure 2. Un nombre mixte transformé en fraction. Source: Wikimedia Commons.

Dans l'image, il y a un exemple de nombre mixte, qui montre la fréquence. Nous avons 2 verres et demi d'eau qui, en tant que nombre mixte, s'exprime comme ceci:

2 ½

Nous obtenons la fraction incorrecte qui le représente:

Supposons maintenant que nous voulons trouver les 3/4 parties de deux verres et demie d'eau. Ce que nous devons faire est de multiplier 3/4 par la fraction incorrecte obtenue:

Il peut vous servir: Distribution de Poisson: formules, équations, modèle, propriétés

Exercices résolus

Exercice 1

Effectuer l'opération suivante:

Solution

Le numéro 1 ¾ est un nombre mixte. Toute sa partie est 1 et sa partie fractionnaire est ¾. Si nous effectuons l'opération: 1 + ¾, le nombre mixte est transformé en une fraction incorrecte.

1 + ¾ = (4 + 3) / 4 = 7/4

Une fois le nombre mixte à partir d'une mauvaise fraction transformée, l'opération de multiplication est effectuée comme d'habitude:

Exercice 2

L'âge de José est de ½ du 2/3 de l'âge de Manuel. Si Manuel a 24 ans, quel est l'âge de José?

Solution

Laissez x l'âge de José, un inconnu que nous devons trouver. La déclaration nous indique que l'âge de Manuel est de 24 ans, donc cette valeur est connue.

Pour déterminer l'âge de José, nous effectuons les opérations indiquées par la déclaration: "L'âge de José est de ½ du 2/3 de l'âge de Manuel".

Ceci est la multiplication de deux fractions pour un entier:

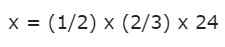
Nous pouvons multiplier les deux premières fractions selon les règles décrites précédemment. Pour sa part, le numéro 24 est un entier, mais nous savons déjà qu'il n'y a aucun problème à le transformer en une fraction, simplement en plaçant un 1 en tant que dénominateur:

Nous pouvons considérablement simplifier l'opération, observant que le 2 dans le numérateur de la deuxième fraction est immédiatement annulé avec le 2 comme un dénominateur dans le premier.

C'est ce que nous avons laissé après l'annulation:

Par conséquent, José a 8 ans.

Les références

1. Baldor, un. 1986. Arithmétique. Éditions et distributions Codex.
2. Carena, m. 2019. Manuel de mathématiques. Université nationale de la côte.
3. Jiménez, R. 2008. Algèbre. Prentice Hall.
4. Mathématiques de Sangaku. Multiplication des fractions. Récupéré de: Sangakoo.com.
5. Smarttick. Multiplication des fractions. Récupéré de: Smartick.est.