Explication de la méthode Gauss-Seidel, applications, exemples

Il Méthode Gauss-Seidel Il s'agit d'une procédure itérative pour trouver des solutions approximatives à un système d'équations algébriques linéaires avec une précision choisie arbitrairement. La méthode s'applique aux matrices carrées avec des éléments non nuls dans ses diagonales et la convergence est garantie si la matrice est dominante en diagonale.

Il a été créé par Carl Friedrich Gauss (1777-1855), qui a fait une démonstration privée à l'un de ses étudiants en 1823. Par la suite, il a été officiellement publié par Philipp Ludwig von Seidel (1821-1896) en 1874, d'où le nom des deux mathématiciens.

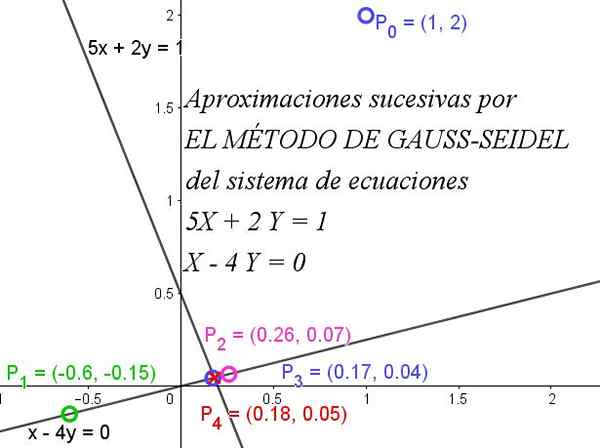
Figure 1. La méthode de Gauss-Seidel converge rapidement pour obtenir un système d'équations. Source: F. Zapata.

Pour une compréhension complète de la méthode, il est nécessaire de savoir qu'une matrice est dominante en diagonale lorsque la valeur absolue de l'élément diagonal de chaque ligne est supérieure ou égale à la somme des valeurs absolues des autres éléments de cette même rangée.

Mathématiquement, il est exprimé comme suit:

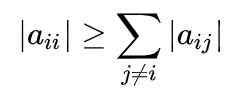
[TOC]

Explication à travers un cas simple

Pour illustrer ce que la méthode Gauss-Seidel prendra un cas simple, dans lequel vous pouvez trouver les valeurs de X et Y dans le système d'équations linéaires 2 × 2 indiqué ci-dessous:

5x + 2y = 1

X - 4y = 0

Pas à suivre

1- Tout d'abord vous avez pour déterminer si la convergence est sûre. Il est immédiatement observé que, en effet, c'est un système dominant en diagonale, car dans la première rangée, le premier coefficient a une valeur absolue plus élevée que les autres de la première rangée:

| 5 |> | 2 |

De même, le deuxième coefficient de la deuxième ligne est également dominant en diagonale:

| -4 |> | 1 |

2- Les variables x et y sont claires: 

X = (1 - 2y) / 5

Y = x / 4

3- Une valeur arbitraire initiale est placée, appelée «graine»: xo = 1, me = 2.

4

Il peut vous servir: estimation par intervalles

X1 = (1 - 2 me) / 5 = (1 - 2 × 2) / 5 = -3/5 

Y1 = x1 / 4 = (-3/5) / 4 = -3/20 

5- Continuez de manière similaire pour obtenir la deuxième approximation de la solution du système d'équations:

X2 = (1 - 2 y1) / 5 = (1 - 2x (-3/20)) / 5 = 13/50 

Y2 = x2 / 4 = (13/50) / 4 = 13/200

6- Troisième itération:

X3 = (1 - 2 y2) / 5 = (1 - 2 (13/200)) / 5 = 87/500

Y3 = x3 / 4 = (87/500) / 4 = 87/2000

7- Quatrième itération, comme itération finale de ce cas illustratif:

X4 = (1 - 2 y3) / 5 = (1 - 2 (87/2000)) / 5 = 913/5000

Y4 = x4 / 4 = (913/5000) / 4 = 913/20000

Ces valeurs coïncident assez bien avec la solution trouvée à travers d'autres méthodes de résolution. Le lecteur peut le vérifier rapidement à l'aide d'un programme mathématique en ligne.

Analyse des méthodes

Comme on peut le voir, dans la méthode Gauss-Seidel, les valeurs approximatives obtenues pour la variable précédente dans cette même étape doivent être remplacées dans la variable suivante. Cela le différencie des autres méthodes itératives telles que Jacobi, dans laquelle chaque étape nécessite les approches de l'étape précédente. 

La méthode de Gauss-Seidel n'est pas une procédure parallèle, tandis que Gauss-Jordan est. C'est aussi la raison pour laquelle la méthode Gauss-Seidel a des étapes sans convergence plus rapides - que la méthode de Jordan.

Quant à l'état de matrice dominante en diagonale, ce n'est pas toujours satisfait. Cependant, dans la plupart des cas, il suffit d'échanger les rangs du système d'origine pour répondre à la condition. De plus, la méthode converge presque toujours, même lorsque la condition de dominance diagonale n'est pas remplie.

Le résultat précédent, obtenu par quatre itérations de la méthode Gauss-Seidel, peut être écrit de manière décimale:

Peut vous servir: combien de axes de symétrie un cercle a-t-il?

X4 = 0,1826

Y4 = 0,04565

La solution exacte au système d'équations soulevées est:

X = 2/11 = 0,1818

Y = 1/22 = 0,04545.

Donc, juste avec 4 itérations, un résultat est obtenu avec un millième de précision (0,001).

La figure 1 illustre comment les itérations successives convergent rapidement vers la solution exacte.

Applications

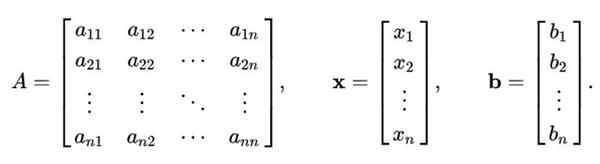
La méthode Gauss-Seidel n'est pas limitée uniquement au système d'équations linéaires 2 × 2. La procédure ci-dessus peut être généralisée pour résoudre un système linéaire de n équations avec n Inconnues, qui est représentée matricielle comme ceci:

POUR X = b

Où POUR C'est une matrice n x n, alors que X Ce sont les composants V vectoriels des variables à calculer; et b C'est un vecteur qui contient les valeurs des termes indépendants.

Pour généraliser la séquence des itérations appliquées dans le cas illustratif à un système N X N, qui souhaite calculer la variable Xi, La formule suivante s'appliquera:

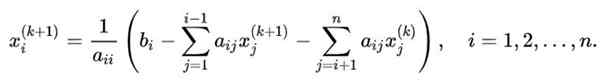
Dans cette équation:

- k C'est l'indice de la valeur obtenue dans l'itération k.

-K + 1 Indique la nouvelle valeur dans ce qui suit.

Le nombre final d'itérations est déterminé lorsque la valeur obtenue dans l'itération K + 1 diffère de l'obtenu immédiatement avant, en un montant ε qui est précisément la précision souhaitée.

Exemples de la méthode Gauss-Seidel

- Exemple 1

Écrivez un algorithme général qui vous permet de calculer le vecteur de solution approximatif X d'un système linéaire d'équations NXN, étant donné la matrice du coefficient POUR, Le vecteur de termes indépendants b, Le nombre d'itérations (iter) et la «graine» initiale du vecteur X.

Solution

L'algorithme se compose de deux cycles "pour", l'un pour le nombre d'itérations et l'autre pour le nombre de variables. Ce serait le suivant:

Pour k ∊ [1 ... iter]

Pour je ∊ [1… n]

X [i]: = (1 / a [i, i]) * (b [i] - ∑_{J = 1}ⁿ(A [i, j] * x [j]) + a [i, i] * x [i])

Peut vous servir: notation décimale

- Exemple 2

Vérifiez le fonctionnement de l'algorithme précédent en postulant à un logiciel mathématique Studio smath gratuit et gratuit, disponible pour Windows et Android. Prenons comme exemple le cas de la matrice 2 × 2 qui nous a permis d'illustrer la méthode Gauss-Seidel.

Solution

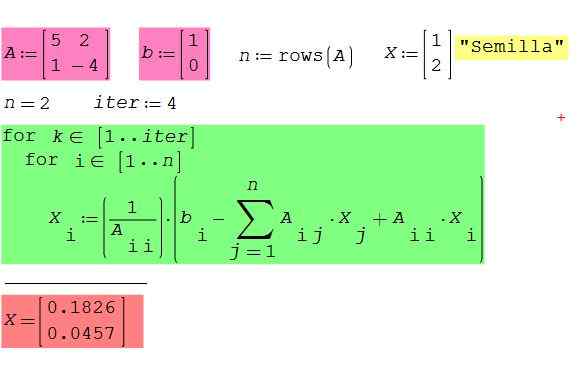Figure 2. Système d'équations de l'exemple 2 x 2, en utilisant un logiciel Studio smath. Source: F. Zapata.

- Exemple 3

Appliquer l'algorithme Gauss-Seidel pour le système d'équations 3 × 3 suivant, qui a déjà été ordonné de telle manière que les coefficients diagonaux sont dominants (c'est-à-dire d'une valeur absolue plus grande que les valeurs absolues des coefficients des coefficients de la même ligne):

9 x1 + 2 x2 - x3 = -2

7 x1 + 8 x2 + 5 x3 = 3

3 x1 + 4 x2 - 10 x3 = 6

Utilisez le vecteur nul comme semence et considérez cinq itérations. Commenter le résultat.

Solution

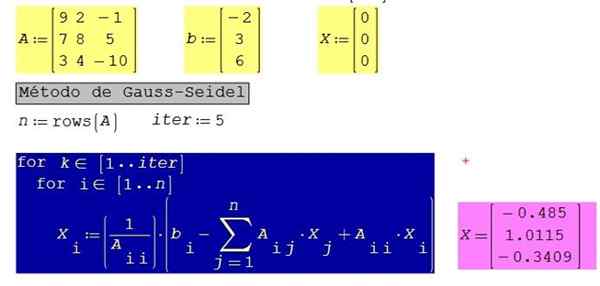figure 3. Solution du système d'équations de l'exemple 3 résolu, en utilisant Smath Studio. Source: F. Zapata.

Pour le même système avec 10 itérations au lieu de 5, les résultats suivants sont obtenus: x1 = -0.485; X2 = 1.0123; X3 = -0.3406

Cela indique qu'il suffit de cinq itérations pour obtenir trois décimales de précision et que la méthode transmet rapidement à la solution.

- Exemple 4

Au moyen de l'algorithme Gauss-Seidel donné, trouvez la solution du système d'équations 4 × 4 qui se produit ci-dessous:

10 x1 - x2 + 2 x3 + 0 x4 = 6

-1 x1 + 11 x2 - 1 x3 + 3 x4 = 25

2 x1 - 1 x2 + 10 x3 - 1 x4 = -11

0 x1 + 3 x2 - 1 x3 + 8 x4 = 15

Pour démarrer la méthode, utilisez cette graine:

x1 = 0, x2 = 0, x3 = 0 et x4 = 0

Considérez 10 itérations et estimez l'erreur du résultat, en comparant avec l'itération numéro 11.

Solution

Figure 4. Solution du système d'équations de l'exemple résolu 4, en utilisant Smath Studio. Source: F. Zapata.

Lorsque vous comparez à l'itération suivante (numéro 11), le résultat est identique. Les plus grandes différences entre les deux itérations sont de l'ordre de 2 × 10^-8, Ce qui signifie que la solution montrée a une précision d'au moins sept décimales.

Les références

1. Méthodes de solution itérative. Gauss-Seidel. Récupéré de: Cimat.mx
2. Méthodes numériques. Gauss-Seidel. Récupéré de: tester.Cua.Uam.mx
3. Numérique: méthode Gauss-Seidel. Récupéré de: Apprenez en linea.toi.Édu.co
4. Wikipédia. Méthode Gauss-Seidel. Récupéré de: dans. Wikipédia.com
5. Wikipédia. Méthode Gauss-Seidel. Récupéré de: est.Wikipédia.com