Mesure approximative des chiffres amorphes Exemple et exercice

La Mesure approximative Des figures amorphes consistent en une série de méthodes utilisées pour déterminer la zone ou le périmètre des figures géométriques qui ne sont pas des triangles, des carrés, des cercles, etc. Certains sont extensibles à des chiffres à trois dimensions.

Fondamentalement, la mesure consiste à faire un réticulé régulièrement, comme les rectangles, les carrés ou les trapèzoïdes, qui couvrent approximativement la surface. La précision de l'approche de la zone obtenue par ces méthodes augmente avec la finesse ou la densité du réticulé.

Figure 1. Des pierres en forme de figures amorphes. Source: pxfuel.

Les figures 1 et 2 montrent diverses figures amorphes. Pour calculer la zone, un réticulé, composé de 2 x 2 carrés, qui à leur tour sont subdivisés en vingt-cinq carrés de 2/5 x 2/5.

Ajout des zones des carrés principaux et des carrés secondaires La zone approximative de la figure amorphe est obtenue.

Figure 2. Un réticulé pour calculer l'aire de l'une des figures amorphes d'une manière approximative. Source: F. Zapata

[TOC]

Zone sous une courbe

Il est souvent nécessaire de calculer la zone sous une courbe entre deux valeurs limites. Dans ce cas, au lieu d'un carré réticulé, les rayures rectangulaires peuvent être tracées approximativement la zone sous ladite courbe.

La somme de toutes les bandes rectangulaires est appelée La somme ou la somme de Riemann. La figure 3 montre une partition de l'intervalle [a, b] sur lequel vous souhaitez déterminer approximativement la zone sous la courbe.

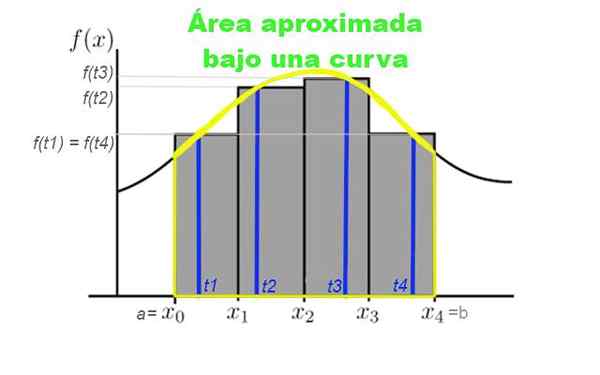figure 3. Partition de l'intervalle [a, b] en quatre sous-intervalles, qui sont généralement tirés de la même largeur. La hauteur des rectangles est déterminée par la valeur de la courbe pour un TK appartenant aux sous-intervalles. Source: F. Zapata.

Supposons que vous souhaitiez calculer la zone sous la courbe donnée par la fonction y = f (x), où x appartient à l'intervalle [a, b] dans lequel vous souhaitez calculer la zone. Pour cela, une partition de n éléments dans cet intervalle est réalisée:

Peut vous servir: 60 diviseurs

Partition = x0 = a, x1, x2, ..., xn = b.

Ensuite, la zone approximative sous la courbe donnée par y = f (x) dans l'intervalle [a, b] est obtenue par la somme suivante:

S = ∑_{K = 1}ⁿ f (t_k) (X_k - X_K-1)

Où t_k est entre x_K-1 et x_k: X_K-1 ≤ t_k ≤ x_k .

La figure 3 montre la somme de Riemann de la courbe y = f (x) dans l'intervalle [x0, x4]. Dans ce cas, une partition de quatre sous-intervalles a été faite et la somme représente la surface totale des rectangles gris. 

Cette somme représente une approche de la zone sous la courbe f entre les abscisses x = x0 et x = x4.

L'approche de la zone sous la courbe s'améliore dans la mesure où le nombre n des partitions est plus grande et a tendance à être exactement la zone sous la courbe lorsque le nombre n les partitions ont tendance à l'infini. 

Dans le cas où la courbe est représentée par une fonction analytique, les valeurs f (t_k) Ils sont calculés d'évaluation de ladite fonction dans les valeurs t_k. Mais si la courbe n'a pas d'expression analytique, les possibilités suivantes restent:

1. Approchez la courbe par une fonction, par exemple un polynôme.
2. Prenez les coordonnées cartésiennes des points où la courbe est interceptée avec les lignes x = t_k.

Intervalles réguliers

En fonction du choix de la valeur TK dans l'intervalle [x_k, X_K-1], la somme peut surestimer ou sous-estimer la valeur exacte de la zone sous la courbe de la fonction y = f (x). La chose la plus recommandée est de prendre le point TK où la zone manquante est approximativement égale à la zone restante, bien qu'il ne soit pas toujours possible de faire un tel choix.  

Peut vous servir: inverse multiplicatif: explication, exemples, exercices résolus

Prenez TK à la fin

La chose la plus pratique est alors d'utiliser des intervalles réguliers de large Δx = (b - a) / n, où a et b sont les valeurs minimales et maximales de l'abscisse, tandis que n est le nombre de subdivisions.

Dans ce cas, la zone sous la courbe s'approche de:

Zone = f (a + Δx) + f (a + 2Δx) +… + f [a + (n-1] Δx + f (b) * Δx

Dans l'expression précédente, Tk a été pris à l'extrémité droite du sous-intervalle.

Prendre Tk à la fin de gauche

Une autre possibilité pratique est de prendre la valeur TK à l'extrémité gauche, auquel cas la somme qui se rapproche de la zone est exprimée:

Zone = [f (a) + f (a + Δx) +… + f (a + (n-1) Δx) * Δx

Tk comme valeur centrale

Dans le cas où TK est choisi comme valeur centrale du sous-intervalle régulier de la largeur de Δx, la somme qui se rapproche de la zone sous la courbe est:

Zone = [f (a + Δx / 2) + f (a + 3Δx / 2) +… + f (b- Δx / 2)] * Δx

L'une de ces expressions tend à la valeur exacte dans la mesure où le nombre de subdivisions est arbitrairement important, c'est-à-dire que Δx tend à zéro, mais dans ce cas, le nombre de termes de la somme est extrêmement important avec le coût de calcul qui en conséquence. 

Exemple

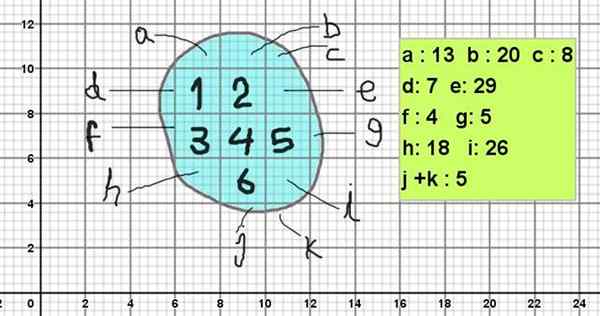
La figure 2 montre une figure amorphe, dont le contour est similaire aux pierres de l'image 1. Pour calculer sa zone, il est placé sur un réticulé avec des carrés principaux de 2 x 2 unités sur le carré (par exemple, ils peuvent être de 2 cm²).

Et comme chaque carré est subdivisé en 5 x 5 subdivisions, chaque subdivision a une superficie de 0,4 x 0,4 unités carrées (0,16 cm²).

Le chiffre du chiffre serait calculé comme suit:

Peut vous servir: Factorisation commune: exemples et exercices

Zone = 6 x 2 cm² + (13 + 20 + 8 + 7 + 29 + 4 + 5 + 18 + 26 + 5) x 0,16 cm²

C'est-à-dire:

Zone = 12 cm² + 135 x 0,16 cm² = 33,6 cm².

Exercice résolu

Calculez approximativement la zone sous la courbe donnée par la fonction f (x) = x² Parie a = -2 jusqu'à b = +2. Pour ce faire, écrivez la somme pour n partitions régulières de l'intervalle [a, b], puis prenez la limite mathématique pour le cas où le nombre de partitions tendent à l'infini. 

Solution

Premièrement, l'intervalle de partition est défini comme 

Δx = (b - a) / n. 

Ensuite, la somme pour la droite correspondant à la fonction f (x) est comme ceci:

A = -2 et b = + 2 est remplacé de sorte que l'intervalle ou l'étape soit Δx = 4 / n. Dans ce cas, la somme de la fonction f (x) = x² est:

 Le binôme carré est développé: 

[-2 + (4i / n)]² = 4 - 16 i / n + (4 / n)² Toi²

Et puis il est remplacé dans la somme:

La séparation des sommations et la prise des quantités constantes en tant que facteur commun de chaque somme sont obtenues:

 La première de la somme, la seconde est:

Et le troisième est:

Remplacement dans l'expression de la somme que vous avez:

S (f, n) = 16 - 64 (n + 1) / 2n + 64 (n + 1) (2n + 1) / 6n²

Lorsque vous choisissez une grande valeur pour n, vous avez une bonne approche de la zone sous la courbe. Cependant, dans ce cas, il est possible d'atteindre la valeur exacte prenant la limite mathématique lorsque N tend à l'infini:

Zone = lim_{N-> ∞}[16 - 64 (n + 1) / 2n + 64 (n + 1) (2n + 1) / 6n²]]

Zone = 16 - (64/2) + (64/3) = 16/3 = 5,333.

Les références

1. Casteleiro, J. M. 2002. Calcul complet (édition illustrée). Madrid: éditorial ESIC.
2. Larson, R. 2010. Calcul d'une variable. 9na. Édition. McGraw Hill.
3. Purcell, E. 2007. Calcul avec géométrie analytique. 9na. Édition. Pearson Education.
4. Monnaie. Histoire du concept d'intégrale. Récupéré de: le référentiel.Monnaie.est
5. UIS. Riemann Sums. Récupéré de: mathématiques.UIS.Édu.co
6. Wikipédia. Zone. Récupéré de: est.Wikipédia.com