Moyen pondéré comment il est calculé, exemples et exercices

La Moyenne pondérée ou moyenne arithmétique pondérée, c'est une mesure de tendance centrale dans laquelle, à chaque valeur x_Toi qui peut prendre une variable x, un peso p est attribué_Toi. En conséquence, en indiquant la moyenne pondérée par x_p, Tu as:

Avec la sommation de la somme, la formule de la moyenne pondérée est:

Où n représente la quantité de valeurs choisies parmi la variable x.

Le p_Toi, qui est également appelé facteur de pondération, C'est une mesure de l'importance que le chercheur attribue à chaque valeur. Ce facteur est arbitraire et toujours positif.

En cela que la moyenne pondérée diffère de la moyenne arithmétique simple, car en cela, chacune des valeurs x_n Il a une signification égale. Cependant, dans de nombreuses applications, le chercheur considère peut-être que certaines valeurs sont plus importantes que d'autres et attribueront un poids en fonction de leurs critères.

Voici l'exemple le plus connu: Supposons qu'un étudiant présente n évaluations dans un sujet et que tous aient le même poids dans la note finale. Dans ce cas, pour calculer la note finale, il suffira de faire une moyenne simple, c'est-à-dire, ajoutez toutes les qualifications et divisez le résultat par n.

Mais si chaque activité a un poids différent, car certains évaluent un contenu plus important ou plus complexe, il sera nécessaire de multiplier chaque évaluation par leur poids respectif, puis ajouter les résultats pour obtenir la note finale. Nous verrons comment effectuer cette procédure dans la section des exercices résolus.

[TOC]

Exemples

Figure 1. La moyenne pondérée est appliquée lors du calcul de l'indice des prix à la consommation, un indicateur d'inflation. Source: pxhere.

L'exemple des qualifications décrites ci-dessus est l'une des plus typiques en termes d'application de la moyenne pondérée. Une autre application très importante en économie est le indice des prix à la consommation soit Indice des prix du consommateur IPC, également appelé panier de famille Et cela sert d'évaluateur de l'inflation dans une économie.

Peut vous servir: angles et triangles

Dans son élaboration, une série d'articles sont prises en compte telles que la nourriture et les boissons non alcoolisées, les vêtements et les chaussures, les médicaments, les transports, les communications, l'éducation, les loisirs et autres biens et services.

Les experts affectent à chaque domaine un facteur de pondération, selon leur importance dans la vie des gens. Les prix sont collectés pendant une période établie, et avec toutes les informations, l'IPC de ladite période est calculée, qui peut être mensuelle, bimontlisée, semestrielle ou annuelle, par exemple.

Le centre de masse d'un système de particules

En physique, la moyenne pondérée a une application importante, qui est de calculer Le centre de masse d'un système de particules. Ce concept est très utile lorsque vous travaillez avec un corps étendu, dans lequel sa géométrie doit être prise en compte.

Le centre de masse est défini comme le point auquel la masse entière d'un objet étendu est concentrée. Sur ce point, les forces peuvent être appliquées comme poids, par exemple, et ainsi expliquer leurs mouvements de traduction et de rotation, à travers les mêmes techniques avec lesquelles ils fonctionnaient lorsque tous les objets étaient censés être des particules.

Par simplicité, il commence à supposer que le corps étendu est composé d'une quantité N de particules, chacun avec une masse m et son propre emplacement dans l'espace: le point de coordonnées (X_Toi, et_Toi, z_Toi).

Être X_Cm La coordonnée X Du centre-ville CM, alors:

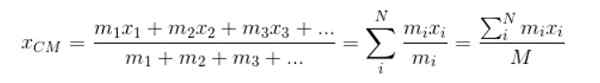
M représente la masse totale du système. Procède à la même manière pour trouver les coordonnées et_Cm et Z_Cm:

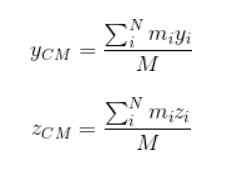
Le facteur de pondération dans ce cas est la masse de chacune des particules qui constituent l'objet étendu.

Peut vous servir: fonctions transcendantes: types, définition, propriétés, exemples

Caractéristiques importantes du centre de masse

Lorsque le nombre de particules est très grand, c'est un objet continu. Dans ce cas, n → ∞ et la somme est remplacée par une intégrale définie, dont les limites sont données par la taille de l'objet.

Il est important de souligner le fait qu'il n'y a pas nécessairement de masse à l'emplacement du centre de masse. Par exemple, dans un beignet de beignet, le centre de masse coïncide plus ou moins avec le centre géométrique de la Rosquilla.

Figure 2. Le centre de masse d'un beignet, un objet assez symétrique, est dans le trou. Source: Pixabay.

L'emplacement du centre de masse ne dépend pas du système de référence utilisé pour établir les positions des particules, car c'est une propriété qui dépend de la configuration de l'objet elle-même et non de la façon dont elle est vue à partir de divers cadres de référence.

Exercices résolus

- Exercice 1

Dans de nombreux cas, les enseignants attribuent des poids ou des pourcentages différents à chaque activité d'évaluation de leur chaise. Ainsi, par exemple, les tâches ont un pourcentage, les autres examens différents et l'examen final-year un probablement beaucoup plus grand.

figure 3. Dans leurs plans d'évaluation, les enseignants attribuent généralement des poids différents aux évaluations. Source: Livre de notes de David Mulder à travers Flickr.

Supposons que dans un certain sujet, les activités d'évaluation et leurs poids respectifs sont les suivants:

-Tâches de la maison: 20%

-Examens courts: 25%

-Rapports de laboratoire: 25%

-Examen final: 30%

a) Comment l'enseignant calcule la note finale de ce sujet pour chaque élève?

b) Supposons que les qualifications d'un étudiant particulier sont, à l'échelle de 1 à 5, ce qui suit:

-Tâches: 5.0 points

-Examens courts: 4.7 points

-Rapports de laboratoire: 4.2 points

-Examen final: 3.5 points

Il peut vous servir: enegon: propriétés, comment faire une égon, exemples

Trouvez la note finale de l'étudiant dans ce sujet.

Solution

a) Chaque évaluation a un poids différent, que l'enseignant a attribué en fonction de sa complexité et de ses propres critères. De cette façon, la note finale est directement calculée comme suit:

Définitif = (x20% Tâches + Examens courts x25% + Rapports x25% + examen final x30%) / 100

b) définitif = (5.0 x 0.2) + (4.7 x 0.25) + (4.2 x 0.25) + (3.5 x 0.3) Points = 4.275 points ≈ 4.3 points

- Exercice 2

Les propriétaires d'un magasin de vêtements ont acheté un jean à trois fournisseurs différents.

Le premier a vendu 12 unités à un prix de 15 € chacun, les 20 secondes de 12 unités à 12.80 € chacun et un tiers ont acheté beaucoup de 80 unités à 11.50 €.

Quel est le prix moyen payé par les propriétaires de magasins pour chaque cow-boy?

Solution

X_p = (12 x 15 + 20 x 12.80 +80 x 11.50) / (12 + 20 + 80) € = 12.11 €

La valeur de chaque cow-boy est 12.11 €, peu importe que certains coûtent un peu plus cher un peu moins. Cela aurait été exactement la même chose si les propriétaires du magasin avaient acheté les 112 jeans à un seul fournisseur qui les aurait vendus en 12.11 € La pièce.

Les références

1. Arvelo, un. Mesures de tendance centrale. Récupéré de: Franarvelo.Wordpress.com
2. Mendenhall, w. 1981. Statistiques pour l'administration et l'économie. 3e. édition. Groupe éditorial IberoAmerica.
3. Moore, D. 2005. Statistiques de base appliquées. 2e. Édition.
4. Triola, m. 2012. Statistiques élémentaires. 11ème. Élégant. Pearson Education.
5. Wikipédia. Moyenne pondérée. Récupéré de: dans.Wikipédia.org