Propriétés de la matrice orthogonale, démonstration, exemples

Tu en as un Matrice orthogonale Lorsque cette matrice s'est multipliée par ses résultats de transposition dans la matrice d'identité. Si l'inverse d'une matrice est égal à la transposition, la matrice d'origine est orthogonale.

Les matrices orthogonales sont caractéristiques que le nombre de lignes est égal au nombre de colonnes. De plus, les vecteurs en ligne sont des vecteurs orthogonaux unitaires et l'éruption des vecteurs transposés sont également.

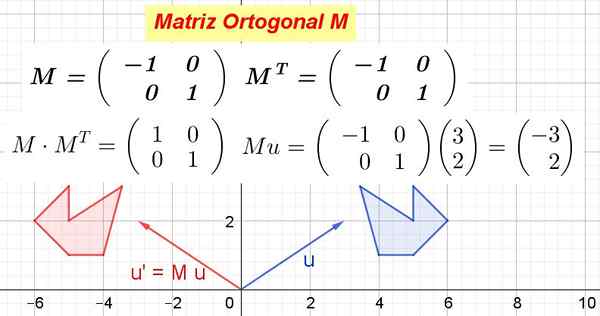Figure 1. Exemple de matrice orthogonale et comment transforme les objets géométriques. (Préparé par Ricardo Pérez)

Lorsqu'une matrice orthogonale est multipliée par les vecteurs d'un espace vectoriel produit un transformation isométrique, c'est-à-dire une transformation qui ne change pas les distances et préserve les angles.

Un représentant typique des matrices orthogonales est le matrices de rotation. Les transformations des matrices orthogonales sur un espace vectoriel sont appelées Transformations orthogonales.

Les transformations géométriques de la rotation et la réflexion des points représentées par ses vecteurs cartésiens sont réalisés en appliquant des matrices orthogonales sur les vecteurs d'origine pour obtenir les coordonnées des vecteurs transformés. C'est pour cette raison que les matrices orthogonales sont largement utilisées dans le traitement graphique de calcul.

[TOC]

Propriétés

Un tableau M Il est orthogonal s'il est multiplié par sa transposition M^T La matrice d'identité se traduit par Toi. De même, le produit de la transposition d'une matrice orthogonale par la matrice d'origine de la matrice d'identité:

M m^T = M^T M = I

À la suite de la déclaration précédente, la transposition d'une matrice orthogonale est égale à sa matrice inverse:

M^T = M^-1.

L'ensemble des matrices de dimension orthogonales n x n Ils forment le groupe orthogonal Ou (n). Et le sous-ensemble de Ou (n) de matrices orthogonales avec détermination +1 Les matrices spéciales regroupent son (n). Matrices du groupe Votre (n) Ce sont des matrices qui produisent des transformations de rotation linéaire, également connues Groupe de rotations.

Manifestation

Nous démontrerons qu'une matrice est orthogonale si, et seulement si les vecteurs de ligne (ou vecteurs de colonne) sont orthogonaux les uns aux autres et de la norme 1.

Peut vous servir: Théorème de Bayes

Supposons que les rangs d'une matrice orthogonale n x n sont n n orthormaux de dimension n. S'il est indiqué par V1, V2,.. ., Vn Le n vecteurs est réalisé:

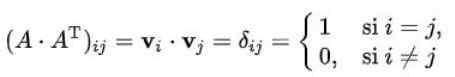
Où il est évident que l'ensemble des vecteurs de ligne est un ensemble de vecteurs orthogonaux avec une norme.

Exemples

Exemple 1

Montrez que la matrice 2 x 2 que le vecteur a dans sa première rangée V1= (-1 0) et dans sa deuxième rangée le vecteur V2= (0 1) est une matrice orthogonale.

Solution: La matrice est construite M et sa transposition est calculée M^T:

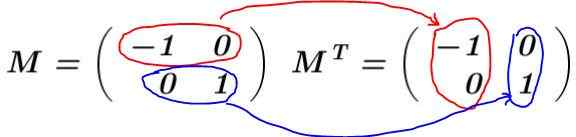
Dans cet exemple, la matrice M C'est une voiture transposée, c'est-à-dire que la matrice et sa transposition sont identiques. Il se multiplie M pour sa transposition M^T:

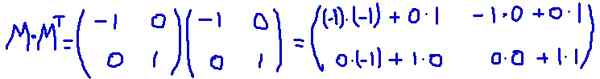
Il est vérifié que M M^T Il est égal à la matrice d'identité:

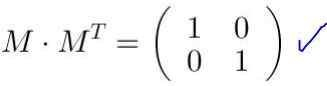
Quand la matrice M Il est multiplié par les coordonnées d'un vecteur ou d'un point, de nouvelles coordonnées sont obtenues qui correspondent à la transformation que la matrice fait sur le vecteur ou le point.

La figure 1 montre comment M Transforme le vecteur ou dans ou' Et aussi comme M Transformez le polygone bleu en polygone rouge. Comme M C'est orthogonal, c'est alors une transformation orthogonale, qui préserve les distances et les angles.

Exemple 2

Supposons que vous avez une matrice 2 x 2 définie dans la reais donnée par l'expression suivante:

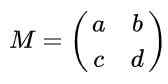
Trouver les valeurs réelles de pour, b, c et d pour que la matrice M Être une matrice orthogonale.

Solution: Par définition, une matrice est orthogonale si elle est multipliée par sa transposition est obtenue en conséquence la matrice d'identité. Rappelant que la matrice transposée est obtenue à partir des lignes d'origine, échangeant des colonnes est l'égalité suivante:

Il peut vous servir: domaine et contradiction d'une fonction (avec des exemples)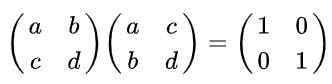

L'exécution de la multiplication matricielle est:

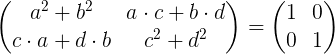
Égalant les éléments de la matrice gauche avec les éléments de la matrice d'identité à droite, nous obtenons un système de quatre équations avec quatre inconnues A, B, C et D.

Nous proposons pour A, B, C et D les expressions suivantes basées sur des raisons trigonométriques Sinus et Cosine:

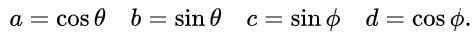
Avec cette proposition et en raison de l'identité trigonométrique fondamentale, la première et la troisième équation de l'égalité des éléments de la matrice est automatiquement satisfaite. Les troisième et quatrième équations sont les mêmes et en égalité de matrice après avoir remplacé les valeurs proposées, c'est ceci:

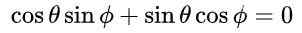
Ce qui mène à la solution suivante:

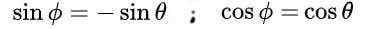
Enfin, les solutions suivantes sont obtenues pour la matrice orthogonale M:

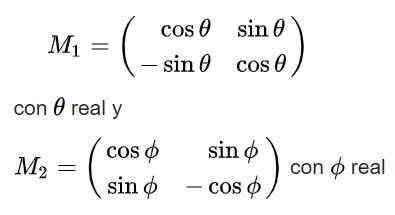
Notez que la première des solutions a un déterminant +1, donc il appartient au groupe ITS (2), tandis que la deuxième solution a un déterminant -1 et n'appartient donc pas à ce groupe.

Exemple 3

Compte tenu de la matrice suivante, trouvez les valeurs de A et B pour avoir une matrice orthogonale.

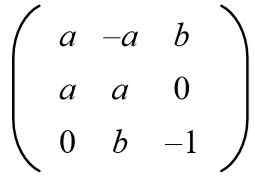
Solution: Pour qu'une matrice donnée soit orthogonale, le produit avec sa transposition doit être la matrice d'identité. Ensuite, le produit matriciel de la matrice donnée avec sa matrice transposée est fabriqué en donnant le résultat suivant:

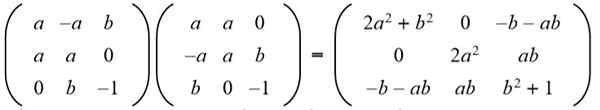
Ensuite, le résultat est adapté à la matrice d'identité 3 x 3:

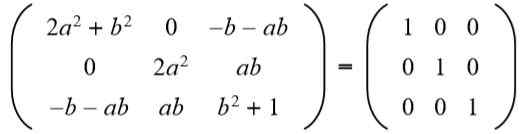
Dans la troisième colonne de deuxième ligne que vous avez (A b = 0), mais pour Cela ne peut pas être nul, car si c'est le cas, l'égalité des éléments de la deuxième ligne et de la deuxième colonne ne serait pas remplie. Alors nécessairement B = 0. Remplacement b Pour la valeur 0 que nous avons:

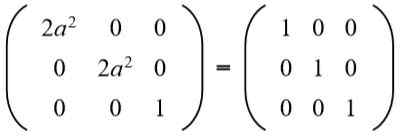
Alors l'équation est résolue: 2a ^ 2 = 1, dont les solutions sont: + ½√2 et -½√2.

Peut vous servir: types d'angles, caractéristiques et exemples

Prendre la solution positive pour pour Il en résulte la matrice orthogonale suivante:

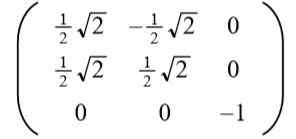
Le lecteur peut facilement vérifier que les vecteurs de lignes (et également les vecteurs de colonne) sont orthogonaux et unit, c'est-à-dire Ortonormal.

Exemple 4

Démontrer que la matrice POUR dont les lignes sont V1 = (0, -1 0), V2 = (1, 0, 0) et V3 = (0 0 -1) C'est une matrice orthogonale. De plus, trouvez comment les vecteurs de la base canonique sont transformés I j k Aux vecteurs U1, U2 et U3.

Solution: Il faut se rappeler que l'élément (i, j) d'une matrice multipliée par sa transposition, est le produit scalaire du vecteur de la ligne (i) par la colonne (j) de la transposition. De plus, ce produit est égal au delta de Kronecker au cas où la matrice serait orthogonale:

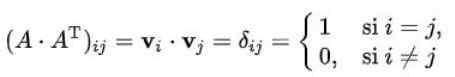
Dans notre cas, c'est comme ceci:

V1 • v1 = 0x0 + (-1) x (-1) + 0x0 = 1

V2 • v2 = 1 × 1 + 0x0 + 0x0 = 1

V3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1

V1 • v2 = 0x1 + (-1) x0 + 0x0 = 0

V2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0

V2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0

V3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0

V1 • v3 = 0x0 + (-1) x (0) + 0x (-1) = 0

V3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0

Avec ce qui est démontré qu'il s'agit d'une matrice orthogonale.

En outre u1 = a i = (0, 1, 0); U2 = a j = (-1, 0, 0) et enfin U3 = a k = (0, 0, -1)

Les références

1. Anthony Nicolaides (1994) Déterminants et matrices. Publication de passage.
2. Birkhoff et MacLane. (1980). Algèbre moderne, Ed. Vicens-vives, Madrid.
3. Casteleiro Villalba M.  (2004) Introduction à l'algèbre linéaire. Éditorial ESIC.
4. Dave Kirkby (2004) Maths Connect. Heinemann.
5. Jenny Olive (1998) Maths: A Student's Survival Guide. la presse de l'Universite de Cambridge.
6. Richard J. Brown (2012) Maths de 30 secondes: les 50 théories les plus exprimées en mathématiques. Ivy Press Limited.
7. Wikipédia. Matrice orthogonale. Récupéré de: est.Wikipédia.com
8. Wikipédia. Matrice orthogonale. Récupéré de: dans.Wikipédia.com