Ligne verticale

Nous expliquons ce qu'une verticale, ses caractéristiques et applications en mathématiques.

Un exemple de ligne verticale

Qu'est-ce qu'une ligne verticale?

Ongle ligne verticale C'est celui qui suit la direction dans laquelle tout objet tombe au sol lorsqu'il est libéré d'une certaine hauteur et est perpendiculaire à la ligne de l'horizon, car il se forme avec cet angle de 90º. 

Lors du dessin, une course est faite de haut en bas ou vice versa. Les bords latéraux de l'écran d'un moniteur d'ordinateur sont des exemples de lignes verticales, ainsi que le tronc droit de nombreux arbres.

Dans l'architecture et la conception, la ligne verticale suggère chez les gens un sentiment de dynamisme, de mouvement, de puissance et d'élévation, contrairement aux lignes horizontales, qui suggèrent le repos et la relaxation. Lorsque quelqu'un est dressé, c'est-à-dire que sa position est verticale et perpendiculaire par rapport au sol, il est prêt à marcher, à courir et en général, entreprendre en mouvement.

Vous pouvez trouver de nombreuses lignes verticales dans l'art, les photographies et les constructions humaines, permanentes ou passagers, telles que celles qui sont formées par des contrastes entre la lumière et l'ombre sur les murs, tout au long de la journée.

La ligne verticale est également utilisée pour décrire un mouvement très commun dans la nature: la chute libre, ainsi que pour décrire la direction d'autres forces, en dehors de la gravité susmentionnée, lorsqu'ils agissent perpendiculairement à une certaine surface.

Forme mathématique de la ligne verticale

En mathématiques et en géométrie, la ligne verticale coïncide avec l'axe cartésien «y», l'axe de la variable dépendante, tandis que l'axe horizontal correspond à l'axe «x», celui de la variable indépendante.

Une ligne verticale peut facilement graphiquement sur le plan cartésien, car il correspond à l'équation:

Peut vous servir: variables statistiques

x = k

Où k est une constante. Les lignes verticales sont toujours parallèles à l'axe y, par exemple la ligne x = −3 qui apparaît en rouge dans la figure suivante:

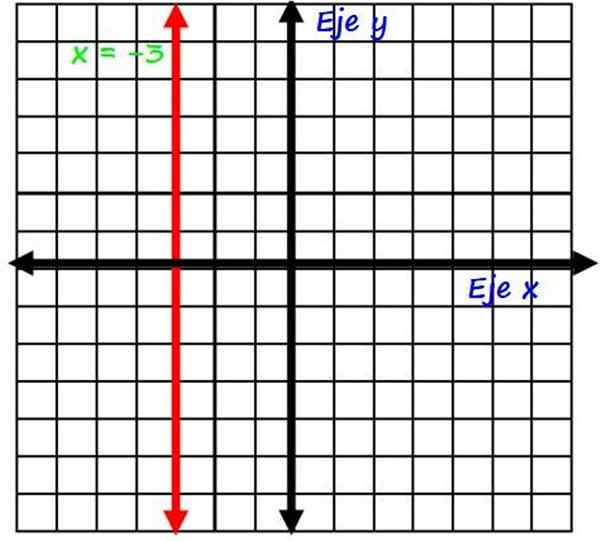Graphique de la ligne verticale x = −3. Source: F. Zapata.

Notez que tous les points de cette ligne ont toujours la même coordonnée x, par exemple les points (−3, 0); (−3, 1), (−3, 2) et plus. De plus, la ligne rouge droite à l'axe horizontal dans la coordonnée x = −3.

D'un autre côté, la ligne d'équation x = 0 est une autre façon d'exprimer l'axe ou l'axe vertical.

Ligne verticale en attente

Il est considéré qu'une ligne verticale manque de pente définie, ou on peut également dire que la ligne verticale a une pente infinie, tandis que la pente d'une ligne horizontale est 0.

Lorsqu'il s'agit d'utiliser la formule pour calculer la pente d'une ligne: m = Δy / Δx Lors du calcul de la pente de la ligne verticale, il arrive que Δx soit toujours égal à 0, car tout point choisi a la même coordonnée x x. N'oubliez pas que Δx = x₂ - X₁, c'est-à-dire la différence entre les coordonnées x de deux points arbitraires.

Ainsi, en essayant de remplacer Δx = 0 dans l'équation de la pente, on constate que:

M = Δy / 0

Et puisque la division de 0 n'est pas une opération définie, il s'avère que la pente de toute ligne verticale est indéfinie, quelle que soit la valeur de Δy.

Test de ligne verticale 

Contrairement à la ligne horizontale, qui est le graphique de la fonction constante, la ligne verticale x = k n'est pas une fonction, car la même valeur de paires infinies de forme commandées avec les valeurs de y, qui va à l'encontre de la définition de la fonction ( En cela, une valeur X a une et une seule image en y).

Peut vous servir: symétrie axiale: propriétés, exemples et exercices

Cependant, la ligne verticale peut être utilisée pour déterminer visuellement si une courbe constitue ou non une fonction. Le critère est très simple: une verticale est tracée qui coupe la courbe en question. Si vous le faites à plus d'un point, ce n'est pas une fonction.

Par exemple, considérez la courbe indiquée ci-dessous, que vous souhaitez savoir si elle correspond au graphique de n'importe quelle fonction.

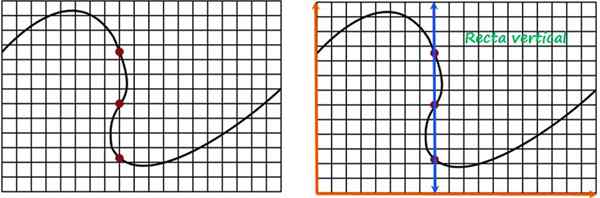Test de ligne verticale pour savoir si une courbe correspond au graphique d'une fonction. Source: F. Zapata.

La même ligne verticale passe par les points rouges et comme il coupe la courbe en plus d'un point, il est conclu que ce n'est pas le graphique d'une fonction.

Asymptotes verticaux

Ce sont des lignes verticales que le graphique d'une fonction ne peut pas traverser. Ils surviennent parce que lorsqu'il aborde une certaine valeur de x, la fonction augmente ou diminue indéfiniment. Bien sûr, cette valeur X n'appartient pas au domaine de la fonction.

En ce qui concerne une fonction rationnelle, les valeurs de x qui proviennent des asymptotes verticales sont celles qui annulent le dénominateur. Dans ce cas, lorsque vous essayez de remplacer cette valeur de X, il y aurait une division entre 0, ce qui n'est pas possible à fonctionner, comme expliqué ci-dessus.

Maintenant, ce qui est possible à faire est de diviser un montant fini d'un autre montant aussi petit que vous le souhaitez, à condition que le montant ne soit pas exactement 0.

Dans de tels cas, le résultat de la division peut être un nombre extrêmement important (ou petit car il est négatif, dépend du signe du numérateur). Le lecteur peut vérifier cela en divisant par exemple:

Peut vous servir: montants vectoriels

2 ÷ 0.000001 = 2 000 000

Supposons que la valeur de x qui annule le dénominateur de la fonction rationnelle est x = b. Lorsqu'une valeur très proche de b (mais pas exactement b) est remplacée dans la fonction, une division entre une quantité finie et une quantité extrêmement petite provient.

C'est pourquoi la fonction rationnelle tend à l'infini positif ou négatif infini au voisinage de l'asymptote verticale, en fonction de la valeur de x utilisée pour aborder b.

Exemple d'asymptote vertical

Ce qui précède est vérifié avec la fonction rationnelle:

La valeur qui annule le dénominateur est x = 2, par conséquent, la fonction a une asymptote verticale sur la ligne x = 2. Supposons que vous souhaitiez aborder x = 2 en prenant une valeur à peine plus petite, par exemple x = 1.9999:

C'était une approche de x = 2 de la gauche et le résultat est que la fonction devient très négative, c'est-à-dire qu'elle a tendance à négatif. Vous pouvez maintenant essayer une approche à droite, par exemple x = 2.0001:

Et on voit que la fonction s'éloigne vers l'infini positif. Le graphique le confirme:

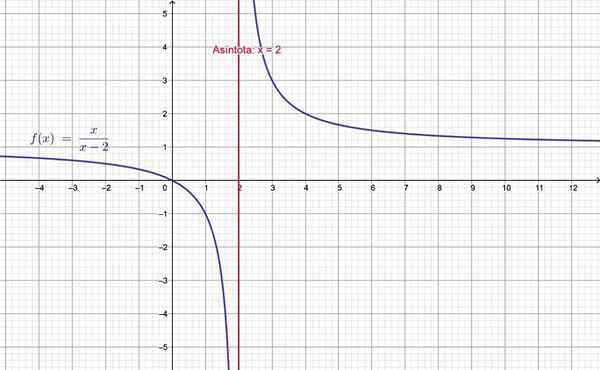La ligne verticale x = 2 est asymptote de f (x). Source: F. Zapata.

Les références

1. Bulletin des enseignants de la conférence de l'Union atlantique. Lignes horizontales et verticales. Récupéré de: Teacherbulintitin.org.
2. Byju's. Ligne verticale. Récupéré de: byjus.com.
3. CK-12. Graphique des lignes horizontales et verticales. Récupéré de: CK-12.org.
4. Stewart, J. 2006. Pré-calcul: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
5. Zill, D. 1984. Algèbre et trigonométrie. 1er. Édition. McGraw Hill.