Homotecia négative

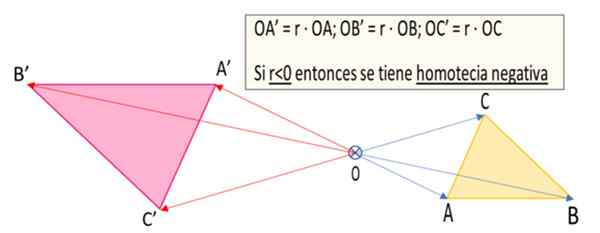
Figure 1. Le triangle a'b'c 'est la transformation homothétique du triangle ABC par rapport au point ou en raison d'homotecia négative r = -1.5 (préparé par: f zapata).

Qu'est-ce que l'homotécia négative?

L'homotécia négative est une transformation dans laquelle un polygone contenu dans un plan a comme image un autre polygone dans ce même plan, d'angles égaux et avec les côtés correspondants proportionnels à ceux de l'original. Lorsque l'homotécia est négative, l'image est tournée d'un demi-tour par rapport à la figure initiale.

L'homotécia se caractérise par un centre d'homotecia SOIT et une constante de proportionnalité appelée raison r. Quand r C'est un nombre négatif, donc on parle d'homotécie négative.

Comment une transformation d'homotecia est-elle faite?

Pour expliquer comment une homotecia négative est effectuée, nous prendrons le cas de la figure 1 dans laquelle un triangle est abc qui veut construire son homothétique négative.

1.- Il commence à choisir un centre d'homotecia, qui est ce cas est le point SOIT.

2.- A partir de SOIT Des segments orientés sont construits (vecteurs) OA, Ob et OC qui vont du centre de l'homotecia à chacun des sommets du triangle.

3.- Une raison d'homotecia est choisie r. Comme vous voulez une homotecia négative, alors r Ça doit être inférieur à zéro. Dans le cas de la figure 1, il a été pris R = -1.5.

4.- Les vecteurs sont dessinés Oa ', Ob ' et OC ', qui sont respectivement Oa '= r ∙ OA, Ob '= r ∙ ob  et OC '= R ∙ OC. Comme R = -1.5, C'est un nombre négatif, puis les vecteurs Oa ', Ob ' et OC ' Ils ont une direction contraire à leurs homologues correspondants, c'est-à-dire OA, Ob et OC. Mais comme la valeur absolue de la raison r est | R | = 1.5 les tailles de Oa ', Ob' et OC ' Ils sont une fois plus élevés que ceux de leurs homologues OA, Ob et OC.

5.- Les pointes des vecteurs Oa ', Ob ' et OC ' définir les sommets du triangle A'b'c ' Quelle est l'homothétique négative du triangle abc.

Propriétés de l'homotécia négative

La homotecia négative, aussi appelé Homotecia inverse, Il a les propriétés suivantes:

Il peut vous servir: Multiples of 8: Que sont et explications

1.- Les côtés correspondants entre le polygone de l'image et le polygone d'origine ont des longueurs proportionnelles, étant la constante de proportionnalité la valeur absolue du rapport homotecia, c'est-à-dire que l'image est amplifiée en un facteur | R | toujours que | R | est supérieur à l'unité, mais l'image est réduite si | R | est moins que l'unité.

2.- Les angles entre les côtés correspondants de l'image et la figure d'origine ont les mêmes mesures.

3.- Les côtés homologues entre l'original et l'image sont parallèles les uns aux autres.

4.- Les segments correspondants dans le cas d'une homotecia négative sont parallèles, mais avec des conseils ou une direction opposée. Par exemple, dans la figure 1, le segment AB a son homologue a'b 'parallèlement au premier, mais avec la direction opposée.

Comparaison avec l'homotecia positive

Il est appelé homotécia positive que dans laquelle le ratio d'homotecia est un nombre positif. Pour construire une homotecia positive, les mêmes étapes sont suivies que celles de l'homotecia négative:

1.- Choisissez un centre d'homotecia, dans notre cas le point SOIT (Voir figure 2).

2.- Dessinez les segments orientés (vecteurs), allant du centre de l'homotécia aux sommets du polygone, dans le cas de la figure 2, ce sont: OA, Ob et OC.

3.- Choisissez un rapport homotecia qui est un nombre positif, par exemple, dans le cas de la figure 2, il a été choisi R = 0.5.

4.- Les vecteurs sont dessinés Oa ', Ob ' et OC ', qui sont respectivement Oa '= r ∙ OA, Ob '= r ∙ ob et OC '= R ∙ OC. Comme r C'est un nombre positif, puis les vecteurs Oa ', Ob ' et OC ' Ils ont la même adresse que OA, Ob et OC. Les longueurs de Oa ', Ob' et OC ' Ils sont à moitié que leurs homologues OA, Ob et OC, Puisque la raison est R = 0.5.

5.- Enfin, les sommets a'b'c 'sont joints pour obtenir le triangle homothétique à ABC avec la raison 1/2.

Peut vous servir: quadrilatère: éléments, propriétés, classification, exemples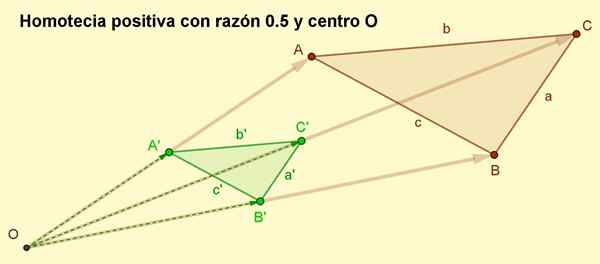 Figure 2. Homotécia positif à juste titre 0,5 des résultats du triangle ABC. Dans une homotécia positive, l'orientation est maintenue. (Préparé par: f. Zapata)

Exemples d'homotecia

L'homotécia apparaît dans diverses situations:

Projecteurs de films

Dans un projecteur de film, l'image enregistrée dans un cadre est projetée et se développe sur un écran, et pour que la projection soit vue à droite, il est nécessaire que le cadre soit investi, car le centre d'homotecia est au centre de l'objectif de lentille de l'objectif du projecteur, entre le cadre et l'écran (homotecia négative, voir figure 3)

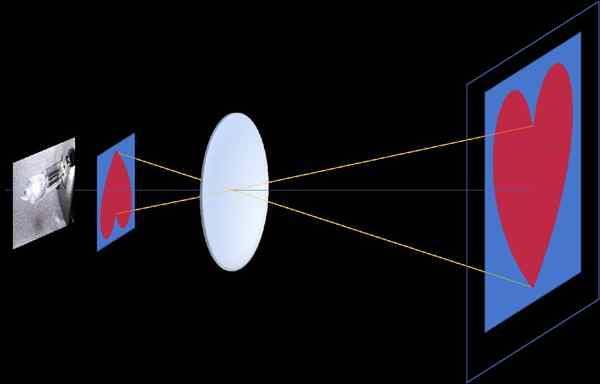figure 3. L'homotecia négative apparaît dans le projecteur de film, entre l'image enregistrée sur un cadre translucide et l'image projetée à l'écran. Le centre d'homotecia se trouve sur le centre optique de l'objectif, à son tour situé entre le cadre et l'écran. Source: F. Zapata.

Caméras photo

Este principio también aplica a las cámaras fotográficas: la luz proveniente de la imagen ubicada a cierta distancia de la lente se proyecta sobre el sensor fotográfico, el cual puede ser una película química sensible a la luz o un sensor CCD, si se trata de una caméra digitale.

L'image enregistrée dans le capteur est inversée par rapport à la vraie et est généralement proportionnellement moins qu'elle.

Application pratique

Le soleil ne doit pas regarder directement, car il cause des dommages permanents à la rétine, mais il y a deux possibilités pour l'étudier: utilisez des filtres qui atténuent l'intensité lumineuse ou projettent son image sur un écran.

Peut vous servir: variation proportionnelle

Un dispositif de projection se compose d'un tube de longueur d. L'une des extrémités du tube est recouverte de papier d'aluminium et de perceuses en son centre avec une épingle. L'autre extrémité, qui servira d'écran, est recouverte de papier translucide, qui peut être du papier d'oignon ou du papier albanène (papier à légumes).

Exercer

Déterminez le diamètre du soleil, sachant que le rayon orbital terrestre est de l'ordre de 150 millions de kilomètres, que le tube de projection, comme celui illustré à la figure 4, a une longueur de 2,2 mètres et que l'image projetée est 2, 1 1 cm de diamètre.

Figure 4. Dans le tube pour projeter le disque solaire, un rapport d'homotecia négatif se produit. Source: F. Zapata.

Solution

Les données sont les suivantes:

• Longueur du tube: D = 2,2 m
• Diamètre d'image projeté du soleil: S = 2,1 cm
• Distance du tube de soleil: r = 150 x 10 ^ 9 m
• Diamètre du soleil réel: S = ¿?

Pour obtenir le diamètre du Soleil, un rapport de proportionnalité est appliqué en fonction de la proportionnalité de l'homotécia (voir figure 4):

La distance au soleil est à la longueur du tube car le diamètre du soleil est au diamètre de l'image projetée:

(R / d) = (s / s)

Effacer cette égalité que le diamètre réel du soleil a le diamètre de la projection multiplié par le quotient entre la distance au soleil et la longueur du tube:

S = S (R / D)

Placer les valeurs numériques est:

S = 2,1 x 10^-2 M (150 x 10⁹ m / 2,2 m)

S = 1,43 x 10⁹ m.

Ce résultat est interprété comme suit: Le diamètre réel du soleil est de 1,43 million de kilomètres.

Les références

1. Álvaro Rendón, à. R. 2004. Dessin technique: cahier d'activité.
2. Antonio Álvarez de la Rosa, J. L. 2002. Affinité, homologie et homotecia.
3. Baer, ​​R. 2012. Algèbre linéaire et géométrie projective. Couer Corporation.
4. Hebert, et. 1980. Mathématiques générales, probabilités et statistiques.
5. MESTERVE, B. ET. 2014. Concepts fondamentaux de la géométrie. Couer Corporation