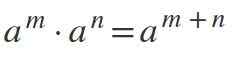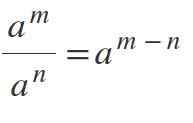Lois des exposants

Quelles sont les lois des exposants?

Le Lois des exposants Ce sont ceux qui s'appliquent à ce nombre qui indiquent combien de fois un numéro de base doit être multiplié par lui-même. Les exposants sont également connus sous le nom de pouvoirs. La potentialisation est une opération mathématique formée par une base (a), l'exposant (m) et la puissance (b), qui est le résultat de l'opération.

Les exposants sont généralement utilisés lorsque de très grandes quantités sont utilisées, car ce ne sont rien d'autre que des abréviations qui représentent la multiplication de ce même nombre une certaine fois. Les exposants peuvent être à la fois positifs et négatifs.

Quels sont les exposants dans les opérations mathématiques?

Comme indiqué ci-dessus, les exposants sont une forme abrégée qui représente la multiplication des nombres pour eux-mêmes, où l'exposant ne se rapporte qu'au numéro de gauche. Par exemple:

2³ = 2 * 2 * 2 = 8

Dans ce cas, le numéro 2 est la base de la puissance, qui sera multipliée 3 fois comme indiqué par l'exposant, situé dans le coin supérieur droit de la base. Il existe différentes façons de lire l'expression: 2 élevée à 3 ou 2 élevée au cube.

Les exposants indiquent également le nombre de fois qui peut être divisé et pour différencier cette opération de la multiplication, l'exposant transporte le signe moins (-) devant lui-même (il est négatif), ce qui signifie que l'exposant est dans le dénominateur de une fraction. Par exemple:

2^{- 4} = 1/2 * 2 * 2 * 2 = 1/16

Cela ne doit pas être confondu avec le cas dans lequel la base est négative, car cela dépendra de la question de savoir si l'exposant est uniforme ou impair pour déterminer si la puissance sera positive ou négative. Ainsi, vous devez:

- Si l'exposant est égal, la puissance sera positive. Par exemple:

(-7)² = -7 _* -7 = 49.

- Si l'exposant est impair, la puissance sera négative. Par exemple:

(-2)⁵ = (-2) * (- 2) * (- 2) * (- 2) * (- 2) = -32.

Il existe un cas particulier dans lequel si l'exposant est égal à 0, la puissance est égale à 1. Il est également possible que la base soit 0; Dans ce cas, selon l'exposant, la puissance sera indéterminée ou non.

Pour effectuer des opérations mathématiques avec des exposants, il est nécessaire.

Quelles sont les lois des exposants?

Première loi: puissance exposante égale à 1

Lorsque l'exposant est 1, le résultat sera la même valeur que la base: A¹ = A.

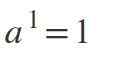
Exemples

9¹ = 9.

22¹ = 22.

895¹ = 895.

Deuxième loi: puissance exposante égale à 0

Lorsque l'exposant est 0, si la base est différente de zéro, le résultat sera: A⁰ = 1.

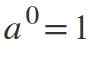
Exemples

1⁰ = 1.

323⁰= 1.

1095⁰ = 1.

Troisième loi: exposant négatif

Comme l'exposant est négatif, le résultat sera une fraction, où la puissance sera le dénominateur. Par exemple, si m est positif, alors^-m = 1 / A^m.

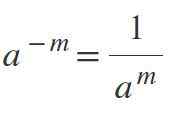
Exemples

- 3^-1 = 1/3.

- 6^-2 = 1/6² = 1/36.

- 8^-3 = 1/8³ = 1/512.

Quatrième loi: multiplication des pouvoirs égaux avec le même

Pour multiplier les pouvoirs où les bases sont identiques et différentes de 0, la base est maintenue et les exposants sont ajoutés: a^m _* pourⁿ = A^{m + n}.    

Exemples

- 4⁴ _* 4³ = 4^{4 + 3} = 4⁷

- 8¹ _* 8⁴ = 8^{1 + 4} = 8⁵

- 2² _* 2⁹ = 2^{2 + 9} = 2^onze

Cinquième loi: Division du pouvoir avec la même base

Pour diviser les pouvoirs dans lesquels les bases sont identiques et différentes de 0, la base est maintenue et les exposants sont soustraits comme suit: un^m / pourⁿ = A^M-n.    

Exemples

- 9² / 9¹ = 9 ^{(vingt-et-un)} = 9¹.

- 6^quinze / 6^dix = 6 ^{(15 - 10)} = 6⁵.

- 49¹² / 49⁶ = 49 ^{(12 - 6)} = 49⁶.

Sixième loi: multiplication de différents pouvoirs avec une base différente

Dans cette loi, il y a l'opposé de ce qui s'exprime dans le quatrième; Autrement dit, si vous avez des bases différentes mais avec les mêmes exposants, les bases sont multipliées et que l'exposant est maintenu: A^m _* b^m = (a_*b) ^m.

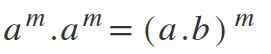
Exemples

- dix² _* vingt² = (10 _* vingt)² = 200².

- Quatre cinq^onze _* 9^onze = (45 * 9)^{11 =} 405^onze.

Une autre façon de représenter cette loi est lorsqu'une multiplication est élevée à un pouvoir. Ainsi, l'exposant appartiendra à chacun des termes: (A_*b)^m= A^m_* b^m.

Exemples

- (5_*8)⁴ = 5⁴ _* 8⁴ = 40⁴.

- (23 * 7)⁶ = 23⁶ _* 7⁶ = 161⁶.

Septième loi: Division du pouvoir différent

Si vous avez des bases différentes mais avec les mêmes exposants, les bases sont divisées et l'exposant est maintenu:^m / b^m = (a / b)^m.

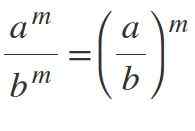
Exemples

- 30³ / 2³ = (30/2)³ = 15³.

- 440⁴ / 80⁴ = (440/80)⁴ = 5,5⁴.

De même, lorsqu'une division est élevée à un pouvoir, l'exposant appartiendra à chacun des termes: (a / b) ^m = A^m / b^m.

Exemples

- (8/4)⁸ = 8⁸ / 4⁸ = 2⁸.

- (25/5)² = 25² / 5² = 5².

Il y a le cas dans lequel l'exposant est négatif. Ainsi, pour être positif, la valeur du numérateur est investie de celle du dénominateur, comme suit:

- (UN B)^-n = (b / a)ⁿ = bⁿ / pourⁿ.

- (4/5) ^-9 = (5/4) ⁹ = 5⁹ / 4⁴.

Huitième loi: pouvoir d'un pouvoir

Lorsque vous avez une puissance qui est élevée à une autre puissance - c'est-à-dire deux exposants en même temps - la base est maintenue et les exposants se multiplient: (A^m)ⁿ= A^{m *n}.

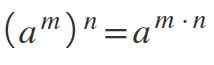
Exemples

- (8³)² = 8 ^{(3 * 2)} = 8⁶.

- (13⁹)³ = 13 ^{(9 * 3)} = 13²⁷.

- (238^dix)¹² = 238^{(10 * 12)} = 238¹²⁰.

Neuvième loi: exposant fractionnaire

Si la puissance a une fraction en tant qu'exposant, ceci est résolu en le transformant en une racine N-Esima, où le numérateur reste comme un exposant et le dénominateur représente l'indice de racine:

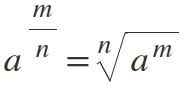
Exemple

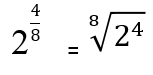
Exercices résolus

Exercice 1

Calculez les opérations entre les pouvoirs qui ont des bases différentes:

2⁴ _* 4⁴ / 8².

Solution

En appliquant les règles des exposants, les bases sont multipliées dans le numérateur et l'exposant est maintenu, comme ceci:

2⁴ _* 4⁴ / 8²= (2_*4)⁴ / 8²  = 8⁴ / 8²

Maintenant, comme il y a des bases égales, mais avec des exposants différents, la base est maintenue et les exposants sont soustraits:

 8⁴ / 8² = 8^{(4 - 2)} = 8²

Exercice 2

Calculer les opérations entre les puissances élevées à une autre puissance:

(3²)³ _* (2 _* 6⁵)^-2 _* (2²)³

Solution

En appliquant les lois, vous devez:

(3²)³ _* (2 _* 6⁵)^-2 _* (2²)³

= 3⁶ _* 2^-2 _* 2^-dix _* 2⁶

= 3⁶ _* 2^{(-2) + (- 10)} _* 2⁶

= 3⁶ _*  2^-12 _* 2⁶

= 3⁶ _* 2^{(-12) + (6)}

= 3⁶ _* 2⁶

= (3_*2)⁶

= 6⁶

= 46.656

Les références

1. Aponte, g. (1998). Fondamentaux de base en mathématiques. Pearson Education.
2. Corbalán, f. (1997). Les mathématiques appliquées à la vie quotidienne.
3. Jiménez, J. R. (2009). Mathématiques 1 sept.
4. Max Peters, W. L. (1972). Algèbre et trigonométrie.
5. Rees, P. K. (1986). Reverre.