Lois de Morgan

Nous expliquons quelles sont les lois de Morgan, nous les montrons et mettons des exemples

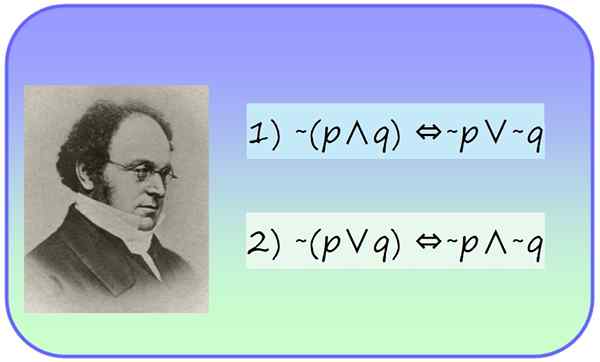Figure 1.- Le mathématicien Auguste de Morgan (1806-1871) et ses lois de la logique propositionnelle. Source: F. Zapata.

Quelles sont les lois de De Morgan?

Les lois de De Morgan sont deux lois logiques appartenant à la logique propositionnelle formulée par le mathématicien anglais Auguste de Morgan (1806-1871). Ils établissent ce qui suit, en ce qui concerne une proposition logique composée:

1. L'opposé d'une conjonction équivaut à la disjonction qui se forme avec les opposés ou les refus des propositions qui composent la conjonction.
2. Le refus de disjonction peut être exprimé comme une conjonction composée des opposés ou des refus des propositions impliquées dans la disjonction.

Dans la notation de la logique propositionnelle, les lois de De Morgan sont exprimées d'une manière compacte et plus formelle comme celle-ci:

1. ∼ (p ∧ q) ⇔ ∼p ∨q
2. ∼ (p ∨ q) ⇔ ∼p ∧q

Ce que ces lois expriment, c'est que, soit dans le déni de conjonction ou de disjonction, le résultat est équivalent à refuser chacune des propositions participantes séparément et à investir le connecteur qui les relie.

Pour une meilleure compréhension des lois de De Morgan, il est nécessaire de revoir le sens des propositions et symboles utilisés dans la logique propositionnelle, pour voir comment ces lois s'appliquent facilement.

Notation logique

L'outil de base de la logique propositionnelle est les propositions. Une proposition logique est une déclaration qui admet un valeur réelle, Que ce soit vrai ou faux, mais pas les deux en même temps. En cette ambiguïté, aucune ambiguïté n'est autorisée, c'est-à-dire qu'il ne peut y avoir aucun doute.

Une proposition est indiquée avec une minuscule, comme dans les exemples suivants:

• Q: Mexico est la capitale du Mexique (vrai).
• Q: En ajoutant 2 et 3, 4 (faux) est obtenu.
• R: Tous les mammifères sont des animaux terrestres (faux).

Peut vous servir: heptagone

Il existe également des propositions plus complexes, qui sont structurées grâce à l'utilisation de propositions simples, telles que celles-ci:

• Q: Carlos ira au cinéma s'il ne pleut pas.
• Q: ANA est chimiste ou biologiste marin.
• R: Juan va dîner ou Pedro verra le jeu à la télévision.

Connecteurs logiques

Les connecteurs logiques sont des symboles utilisés pour relier les propositions simples et créer ainsi des propositions plus complexes. Dans la logique propositionnelle, chacun a une signification particulière.

Les connecteurs les plus utilisés sont la conjonction, la disjonction, la disjonction exclusive, le déni, la conditionnalité et la bi-conditionnalité.

Conjonction

La conjonction est indiquée avec une lettre "V" inversée. Une proposition composite par une conjonction est symbolisée p ∧ Q, comme suit:

• P ∧ Q: Mexico est la capitale du Mexique et se trouve en Amérique du Nord.

Il est facile d'identifier ici que P est "Mexico est la capitale du Mexique" et Q est "est en Amérique du Nord".

Disjonction

Deux types de disjonction se distinguent: les faibles et les exclusives. Ongle faible disjonction Il est symbolisé par ∨ et en notation logique, ce serait p ∨ q. L'exemple de ce type de disjonction est:

• P ∨ Q: Juan est footballeur ou Juan est un joueur de tennis.

Au lieu de cela, le disjonction exclusive Il est symbolisé par le signe ⊻ et implique que l'une des propositions doit être exclue, par exemple:

P ⊻ Q: Alicia a 20 ans ou Alicia a 22 ans.

La différence entre les deux types est claire, dans une disjonction exclusive, l'une des propositions est exclue, car si Alicia a 20 ans, il ne peut pas être 22 et vice versa. D'un autre côté, dans la faible disjonction, Juan peut être un footballeur et un joueur de tennis en même temps.

Le déni

En mettant le symbole ∼ une proposition, ceci est refusé, comme dans:

• Q: ∼ (Veracruz est la capitale du Mexique).

Qui est lu comme "Veracruz n'est pas la capitale du Mexique". D'autres façons d'exprimer un déni, à part "non", est à travers des phrases comme "est fausse", "c'est un mensonge que" et "Ce n'est pas vrai".

Peut vous servir: interpolation linéaire

Conditionnalité

Ce sont des propositions composites qui utilisent généralement les mots "oui" et "alors ..." pour lier deux propositions dans lesquelles il y a une conditionnalité ou implication. La partie de la proposition écrite immédiatement après le "oui" est le antécédent vague hypothèse de la proposition et ce qui est après le terme "alors" conclusion soit conséquent.

Le symbole utilisé pour la conditionnalité est la flèche de gauche à droite "→", donc une conditionnalité entre deux propositions est représentée comme P → Q, qui peut être lue comme "si p, alors q" ". Par exemple:

P → Q: S'il pleut pendant l'après-midi, je ne jouerai pas au tennis.

Biditionnalité

Dans ce type de proposition, la phrase «oui, et seulement si» pour connecter deux propositions, appelée premier et deuxième membre biconditionnel est utilisé. Le symbole utilisé est la flèche bidirectionnelle "↔".

Les deux propositions liées par "Oui, et seulement si" sont appelées respectivement premier et deuxième membre et la bi-conditionnalité de deux propositions P et Q reste comme P ↔ Q. Par exemple:

P ↔ Q: Maria aime faire du vélo si et seulement si la journée est ensoleillée.

Démonstration des lois de De Morgan

Les lois de De Morgan font partie des équivalences logiques et peuvent être démontrées à travers les tables de vérité, qui sont utilisées pour connaître la valeur de vérité (vraie ou fausse) d'une proposition.

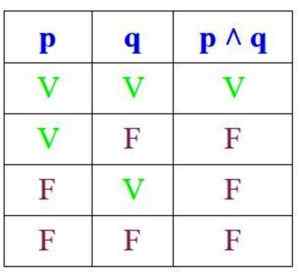
Puisque la conjonction n'est vraie que lorsque P et Q sont vraies, sa table de vérité est:

D'un autre côté, en disjonction, la proposition est vraie si P et Q sont vraies ou si au moins l'un d'entre eux l'est, mais il est faux si les deux sont:

Peut vous servir: permutations sans répétition: formules, démonstration, exercices, exemples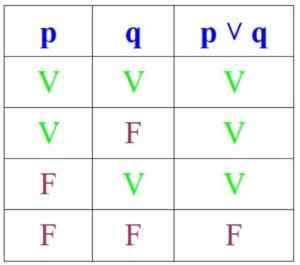

Maintenant, Denial transforme la vérité en faux et vice versa. Dans ce cas, les valeurs de vérité de ∼ (p ∧ q) et ∼ (p ∨ q) sont l'opposé des valeurs de vérité (p ∧ q) et (p ∨ q):

Et il faut vérifier que ces résultats sont obtenus lors de la réalisation des tables de vérité respectives de (∼ P ˅ ∼ Q) et (∼ P ˄ ∼ Q):

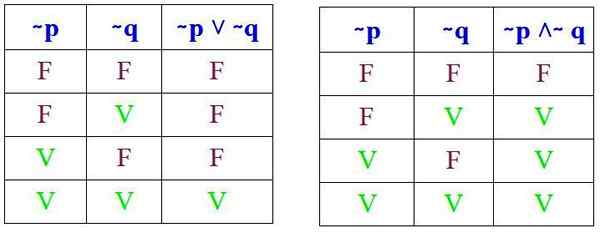
Et en effet, lorsque vous comparez les tables de vérité respectives, il est observé que les lois de De Morgan sont remplies. Maintenant, deux exemples de sa demande seront vus.

Exemple résolu 1

Appliquez les lois de De Morgan pour trouver l'expression équivalente de: ∼ (∼P ˅ ∼Q)

• Solution

L'expression donnée est comparée ∼ (∼P ˅ ∼Q) avec la loi de Morgan:

∼ (p ∨ q) ⇔ ∼p ∧q

Et il est observé que le déni est déjà en dehors de la parenthèse dans les deux cas, donc les instructions de la loi sont suivies: il refuse ∼P, nie ∼Q et le connecteur est modifié:

∼ (∼p ˅ ∼q) ⇔ ∼ (∼p) ∧ ∼ (∼q) ⇔ p ∧ q

Exemple résolu 2

Déterminez l'expression équivalente de ∼ [∼P ˄ ∼ (∼q)] ≡

• Solution

Premièrement, le déni de ∼Q est simplifié:

∼ [∼p ˄ ∼ (∼q)] ⇔ ∼ [∼p ˄ q]

Comme il y a déjà un déni en dehors du support, l'expression résultante est comparée à la loi de Morgan: ∼ (p ∧ q) ⇔ ∼p ∨q

Pour résoudre ∼ [∼P ˄ Q], vous devez nier ∼P, nier Q et modifier le connecteur:

∼ [∼p ˄ q] ⇔∼ (∼p) ∨ ∼q ⇔ p ˅ ∼q

Les références

1. Becerra, J.M.  Notes logiques Unam.
2. Brillant. Des lois de Morgan. Récupéré de: brillant.org.
3. Tutoriels électroniques. Par le théorème de Morgan. Récupéré de: électronique-Tormales.WS.
4. López, f. Introduction à la logique mathématique. Récupéré de: youtube.com
5. Muñoz, C. Introduction à la logique. Récupéré de: sites Web.Ucm.est.