La loi de Watt qu'est-ce que, des exemples, des applications

La Loi de Watt Il s'applique aux circuits électriques et établit cette puissance électrique P fourni par un élément de circuit, il est directement proportionnel au produit entre la tension d'alimentation V du circuit et de l'intensité de courant Toi qui circule à travers lui.

La puissance électrique est un concept très important, car il souligne à quelle vitesse il est un élément de transformer l'électricité en une autre forme d'énergie. Mathématiquement, la définition donnée de la loi de Watt est exprimée comme suit:

P = V.Toi

Figure 1. La puissance électrique indique la vitesse à laquelle l'électricité est transformée. Source: Pixabay

Dans le système des unités internationales (SI), l'unité d'alimentation est appelée Watt Et il est abrégé w, en l'honneur de James Watt (1736-1819), un ingénieur écossais pionnier de la révolution industrielle. Étant donné que la puissance est de l'énergie par unité de temps, 1 W est égal à 1 joule / seconde.

Nous connaissons tous le concept d'énergie électrique d'une manière ou d'une autre. Par exemple, les dispositifs électriques à domicile à usage commun apportent toujours leur puissance spécifiée, y compris les ampoules, les couchettes électriques ou les réfrigérateurs, entre autres.

[TOC]

Watt Law and Circuit Elements

La loi de Watt s'applique aux éléments de circuit avec un comportement différent. Cela peut être une batterie, une résistance ou un autre. Parmi les extrémités de l'élément, une différence de potentiel est établie V_B - V_POUR = V_{UN B} Et le courant circule dans le sens de A à B, comme indiqué dans la figure suivante:

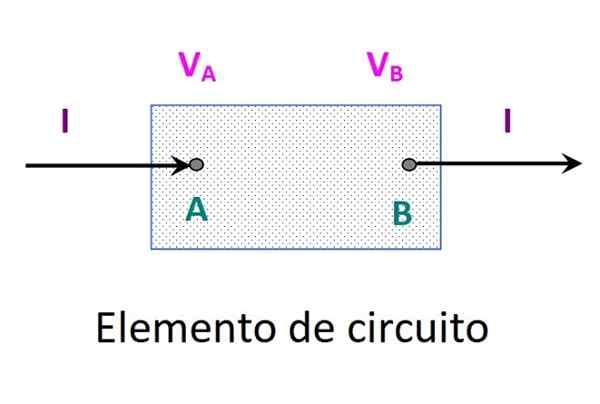Figure 2. Un élément de circuit dans lequel une différence de potentiel a été établie. Source: F. Zapata.

Dans un très petit temps Dt, Passer une certaine charge dq, Pour que le travail effectué soit donné par:

dw = v.dq

Où dq Il est lié au courant AS:

dq = i.Dt

Ensuite:

Peut vous servir: nain rouge

dw = v. Toi.Dt

dw / dt = v. Toi

Et puisque la puissance est un travail par unité de temps:

P = V.Toi

-Oui V_{UN B} > 0, les charges qui traversent l'élément gagnent de l'énergie potentielle. L'élément fournit de l'énergie à partir d'une source. Ce pourrait être une batterie.

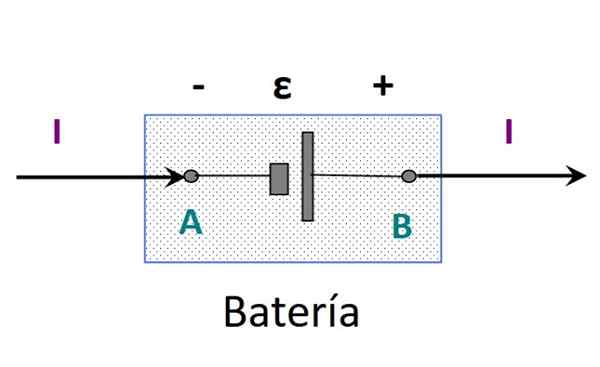figure 3. Énergie fournie par une batterie. Source: F. Zapata.

-Oui V_{UN B} < 0, las cargas pierden energía potencial. El elemento disipa energía, tal como una resistencia.

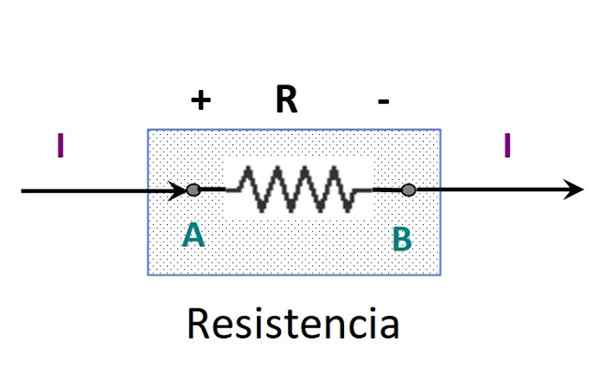Figure 4. La résistance transforme l'énergie sous forme de chaleur. Source: F. Zapata.

Notez que l'alimentation fournie par une source ne dépend pas uniquement de la tension, mais aussi du courant. Ceci est important pour expliquer pourquoi les batteries de voitures sont si grandes, en tenant compte qu'elles fournissent à peine 12 V.

Ce qui se passe, c'est que le moteur de démarrage a besoin d'un courant élevé, pendant une courte période, qui fournit la puissance nécessaire pour démarrer la voiture.

La loi Watt et la loi d'Ohm

Si l'élément de circuit est une résistance, la loi de Watt et la loi d'Ohm peuvent être combinées. Ce dernier établit cela:

V = i. R

Qu'en remplaçant la loi de Watt mène à:

P = V. I = (i.R).I = i².R

Une version basée sur la tension et la résistance peut également être obtenue:

P = V. (V / r) = v² / R

Les combinaisons possibles entre les quatre amplitudes: puissance P, courant I, tension V et résistance R. Selon les données proposées par un problème, les formules les plus pratiques sont choisies.

Par exemple, supposons que dans un certain problème, il est demandé de trouver la résistance R, qui se trouve dans la pièce en bas à gauche de la lettre.

Selon les amplitudes dont la valeur est connue, certaines des trois équations connexes (en vert) sont choisies (en vert). Par exemple, supposons qu'ils se connaissent V et Toi, ensuite:

Peut vous servir: PASCAL PRINCIPE: HISTOIRE, applications, exemples

R = v / i

S'ils sont connus P et Toi, Et la résistance est demandée, utilisée:

R = p / i²

Enfin, quand ils se connaissent P et V, La résistance est obtenue par:

R = p² / V

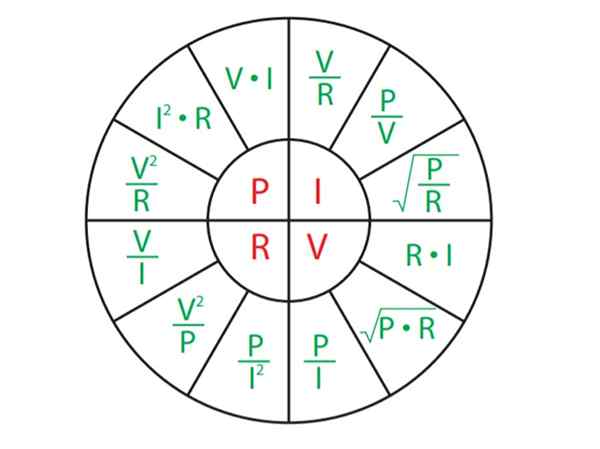Figure 5. Watt Law Formules et OHM's Law. Source: F. Zapata.

Applications

La loi de Watt peut être appliquée dans des circuits électriques pour trouver l'alimentation électrique fournie ou consommée par l'élément. Les ampoules sont de bons exemples d'application de la loi de Watt.

Exemple 1

Une ampoule spéciale pour obtenir plusieurs illuminations en un, a deux filaments de tungstène, dont les résistances sont R_POUR = 48 ohm et r_B = 144 ohm. Ils sont connectés à trois points, désignés par 1, 2 et 3, comme on le voit dans la figure.

L'appareil est contrôlé par des commutateurs pour sélectionner les paires de bornes et la connecter également au réseau 120 V. Trouvez tous les pouvoirs possibles qui peuvent être obtenus.

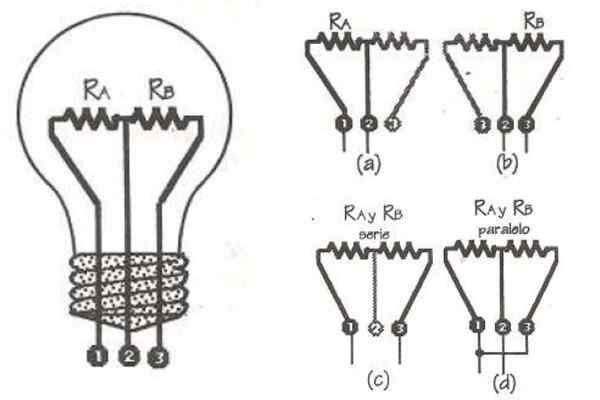Figure 6. Schéma pour l'exemple résolu 1. Fontaine. D. FigUeroa. Physique pour la science et l'ingénierie.

Solution

- Lorsque les bornes 1 et 2 se connectent, seule résistance R_POUR Il est activé. Étant donné que la tension est obtenue, qui est de 120 V et la valeur de la résistance, ces valeurs sont directement remplacées dans l'équation:

P = V²/ R = (120 V)²/ 48 ohm = 300 W

- Les bornes de connexion 2 et 3, la résistance R est activée_B, dont le pouvoir est:

P = V²/ R = (120 V)²/ 144 ohm = 100 W

- Les bornes 1 et 3 permettent de connecter les résistances en série. La résistance équivalente est:

R_égaliseur = R_POUR + R_B = 48 ohm + 144 ohm = 192 ohm

Donc:

P = V²/ R = (120 V)² / 192 ohm = 75 W

- Enfin, la possibilité restante est de connecter la résistance en parallèle, comme indiqué dans le diagramme d). La résistance équivalente dans ce cas est:

1 / r_égaliseur = (1 / r_POUR) + (1 / r_B) = (1/48 ohm) + (1/144 ohm) = 1/36 ohm.

Par conséquent, la résistance équivalente est R_égaliseur = 36 ohm. Avec cette valeur, la puissance est:

Peut vous servir: propriétés électriques des matériaux

P = V² / R = (120 V)² / 36 ohms = 400 W

Exemple 2

En plus du WATT, une autre unité largement utilisée pour la puissance est le kilowatt (ou kilowatt), abrégé en KW. 1 kW est égal à 1000 watt.

Les entreprises qui fournissent une facturation électrique aux maisons en termes d'énergie consommée, et non de la puissance. L'unité qu'ils utilisent est le kilowatt-hora (kw-h) qui, malgré le nom de Watt, est l'énergie pour l'énergie.

1 kilowatt-hora ou kw-h C'est l'énergie fournie en 1 heure par une puissance de 1000 watt, qui en Joules serait équivalente à:

1 kW-h = 1000 W x 3600 s = 3.6 x 10 ⁶ J

A) Supposons qu'une maison consomme 750 kWh pour un certain mois. Quel sera le montant de la facture d'électricité de ce mois? Le plan de consommation suivant suit:

- Taux de base: 14 $.00.

- Prix: 16 cents / kWh jusqu'à ce que vous atteigniez 100 kWh par mois.

- Les 200 kWh suivants par mois ont une valeur de 10 cents / kWh.

- Et plus de 300 kWh par mois, 6 cents sont facturés / kWh.

b) Trouvez le coût moyen de l'électricité.

Solution à

- Le client consomme 750 kW-h par mois, dépasse donc les coûts indiqués à chaque étape. Pour les 100 premiers kWh, la valeur monétaire est: 100 kWh x 16 cents / kWh = 1600 cents = 16.00 $

- Les 200 kWh suivants ont un coût de: 200 kWh x 10 cents / kWh = 2000 cents = 20.00 $.

- Au-dessus de ces 300 kW-h, le client consomme 450 kW-h de plus, pour un total de 750 kW-h. Le coût dans ce cas est: 450 kWh x 6 cents / kWh = 2700 cents = 27.00 $.

- Enfin, tous les montants obtenus plus le taux de base sont ajoutés, pour obtenir le prix de la réception de ce mois:

Prix ​​à payer = 14.00 $ + 16.00 $ +20.00 $ + 27.00 $ = 77 $.

Solution B

Le coût moyen est: 77 $ / 750 kWh = 0.103 $ / kw-h = 10.3 cents / kWh.

Les références

1. Alexander, C. 2006. Fondations du circuit électrique. 3e. Édition. McGraw Hill.
2. Berdahl, e. Introduction à l'électronique. Récupéré de: CCRMA.Stanford.élégant.
3. Boylestad, R. 2011. Introduction à l'analyse des circuits. 13e. Édition. Pearson.
4. Association du reconstruction électrique. La calculatrice de la loi de la loi et de Watt d'Ohm avec l'exemple. Récupéré de: ElectricalRebuilders.org
5. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 5. Électricité. Édité par Douglas Figueroa (USB).