Loi des proportions multiples

Quelle est la loi de plusieurs proportions?

La Loi des proportions multiples Il établit que si deux éléments forment plus d'un composé lorsqu'ils réagissent les uns aux autres, alors la proportion des masses avec lesquelles l'une d'entre elles est combinée avec une masse fixe de l'autre, il est égal à une relation de petit nombre.

L'énoncé de la loi peut sembler complexe si vous n'avez pas d'exemple à portée de main. Considérez donc certains biscuits Oreos, composés de deux couvercles de chocolat et une bande de crème sucrée: t₂C (t = couvercle et c = crème). Si nous voulions inventer un biscuit Oreo plus robuste, nous ajouterions une autre bande de crème, afin d'avoir une double crème (t₂C₂ ou tc).

Dans les desserts, comme les cookies Oreos, nous avons des proportions qui peuvent être variées simplement pour en préparer d'autres versions. Source: Brokensphere, CC BY-SA 3.0 https: // CreativeCommons.Org / licences / by-sa / 3.0 via Wikimedia Commons

Nous pourrions également en ajouter un autre, afin que le cookie ait trois fois plus de crème qu'un biscuit conventionnel (t₂C₃). Et si nous mettons un autre couvercle de chocolat au milieu des rayures blanches (t₃C₂)? Les options sont illimitées; Mais nous ajoutons toujours une unité de couvercle ou de crème. Nous ne pensons pas à la moitié du couvercle (1/2 t), ni à un cinquième de crème (1/5 C), car ce serait inapproprié.

De la même manière que cela se produit avec les éléments chimiques: leurs atomes ne se divisent pas pour former des composés. Par conséquent, les masses de T ou C parmi leurs composés "toujours" une relation simple.

Explication

Proportions

La loi de plusieurs proportions, ainsi que la loi des proportions définies, ont précédé la stoechiométrie et les premières formules chimiques. Oublions les cookies, mais gardons leurs symboles: T et C. Grâce aux expériences, il est découvert que les éléments T et C forment plusieurs composés: t₂C, TC et T₂C₃.

Avant les formules chimiques, il était impossible de savoir immédiatement qui étaient les proportions des masses de T et C dans de tels composés. A dû les déterminer d'abord. Dans un composé, il a été découvert que la masse de T a doublé à celle de C; Pour dire, 2 grammes de t sont combinés avec 1 gramme de C.

Peut vous servir: Capacité: unités, formules, calcul, exemples

Ensuite, dans l'autre composé, les masses de T et C devaient être appariées: 2 grammes de T sont maintenant combinés avec 2 grammes de C. Ici, la question se pose: et si T et C peuvent toujours former un autre composé? Si c'est le cas, il serait sûrement formé avec 2 grammes de T, mais cette fois, ils seraient combinés avec 3 grammes de C (1 gramme + 1 gramme + 1 gramme).

Relations de masse simples

Les proportions des masses avec lesquelles T et C réagissent permettent d'établir leurs formules chimiques: T₂C (2 grammes T: 1 gramme C), TC (2 grammes T: 2 grammes C) et T₂C₃ (2 grammes T: 3 grammes C). Si nous voulons comparer les relations des masses T ou C dans ces composés, il est nécessaire que l'une de ses masses reste constante; Dans ce cas, celui de T: 2 grammes.

Par conséquent, nous déterminerons les proportions de masse de C dans ces trois composés:

• T₂C: 1 gramme C / 2 grammes T
• TC: 2 grammes c / 2 grammes t
• T₂C₃: 3 grammes c / 2 grammes t

Nous aurons une relation pour la masse de C égale à 1: 2: 3. C'est-à-dire qu'il y a 2 fois plus C en tc que dans t₂C, et 3 fois plus C en t₂C₃ que dans t₂C. Comme on peut le voir, 1: 2: 3 sont de petits nombres entiers (ils ne dépassent même pas la douzaine).

Exemples de la loi de plusieurs proportions

Pour les exemples suivants, les mêmes étapes précédentes seront appliquées, mais nous prendrons en compte les masses molaires des éléments respectifs, en supposant une mole du composé.

NOIX DE COCO₂

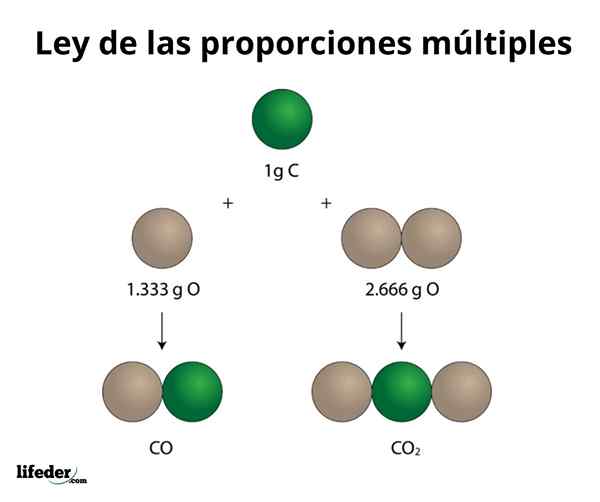
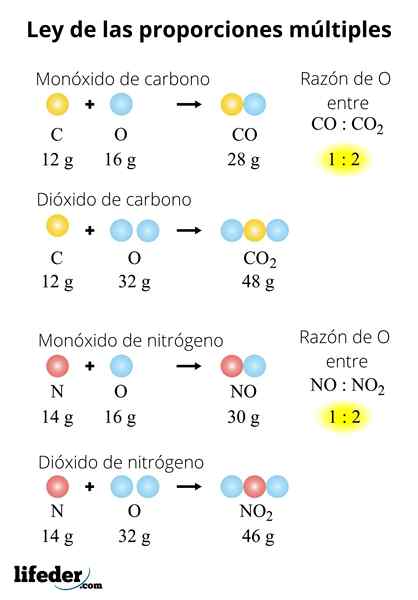
Cet exemple explique de manière simple comment fonctionne la loi des proportions multiples; Dans le CO (monoxyde de carbone), il y en a 1.333 grammes d'oxygène pour chaque gramme de carbone. Dans le dioxyde de carbone (CO₂), il y en a 2.666 grammes d'oxygène pour chaque gramme de carbone. Par conséquent, la proportion d'oxygène dans les deux composés est de 1: 2, un petit nombre entier.

H₂OH₂SOIT₂

La loi sur les proportions multiples s'applique à la paire de h₂OH₂SOIT₂.

Peut vous servir: 30 exemples de suspensions chimiques

Dans une mol de h₂Ou 2 grammes d'hydrogène sont combinés avec 16 grammes d'oxygène. Pendant ce temps, dans une mol de h₂SOIT₂, 2 grammes d'hydrogène sont combinés avec 32 grammes d'oxygène. Pour vérifier si cette loi est remplie, nous devons définir la même masse pour l'un des éléments dans les deux composés. Cette fois est l'hydrogène: 2 grammes.

Proportions de masse pour h₂Ou et h₂SOIT₂ ils sont:

• H₂O: 16 grammes ou / 2 grammes H
• H₂SOIT₂: 32 grammes ou / 2 grammes H

Le rapport de la masse d'O sera de 16:32. Cependant, nous pouvons le simplifier en divisant par 16, en restant 1: 2. Encore une fois, la relation finale est composée de petits nombres entiers.

Swin₂-Swin₃

Dans une mol de SO₂, 32 grammes de soufre sont combinés avec 32 grammes d'oxygène. Pendant ce temps, dans une mol de SO₃, 32 grammes de soufre sont combinés avec 48 grammes d'oxygène. La masse de soufre est la même pour les deux composés, nous pouvons donc comparer directement les proportions d'oxygène:

• Swin₂: 32 grammes ou
• Swin₃: 48 grammes ou

Étant le rapport de la masse d'oxygène entre les deux composés égaux à 32:48 ou 1: 1.5. Mais n'étaient pas là qu'il devrait y avoir des nombres entiers? Relation 1: 1.5 (1/1.5) Il peut également être écrit comme 2: 3 (0.6), et encore une fois, nous aurons de petits nombres entiers: 2 et 3.

Notez que nous aurions également pu écrire la relation à 48:32 ou 1.5: 1, étant le résultat 3: 2. La loi ne change pas, seulement l'interprétation de la relation: il y a 1.5 ou 3/2 fois plus d'oxygène dans le SO₃ que dans le so₂; qui est la même chose pour dire qu'il y a 2/3 ou 0.6 fois moins d'oxygène dans le SO₂ que dans le so₃.

NON NON₂-N₂SUR₂SOIT₃-N₂SOIT₅

La loi peut également être appliquée à une série de composés. Considérez les oxydes d'azote: non pas₂-N₂SUR₂SOIT₃-N₂SOIT₅. Afin d'évaluer cette loi en eux, nous devons définir une masse d'azote: 28 grammes. Parce que? Parce que non et non₂ Ils ont un atome d'azote moins que les autres oxydes:

• 2 (non): 28 grammes n / 32 grammes ou
• 2 (non₂): 28 grammes n / 64 grammes ou
• N₂O: 28 grammes n / 16 grammes ou
• N₂SOIT₃: 28 grammes n / 48 grammes ou
• N₂SOIT₅: 28 grammes n / 80 grammes ou

Il peut vous servir: acide hypophysaire (H3PO2): propriétés, utilisations et réactifs

Oublions l'azote et concentrons-nous sur les grammes d'oxygène:

• 2 (non): 32 grammes ou
• 2 (non₂): 64 grammes ou
• N₂O: 16 grammes ou
• N₂SOIT₃: 48 grammes ou
• N₂SOIT₅: 80 grammes ou

Étant le rapport des masses de ou égal à 32: 64: 16: 48: 80. Pour le simplifier, nous divisons tous ses chiffres parmi les plus petits, le 16, étant 2: 4: 1: 3: 5.

C'est-à-dire qu'il y a: 2 fois plus d'oxygène dans le non que dans le n₂Ou, 4 fois plus d'oxygène dans le non₂ que dans le n₂Ou, 3 fois plus d'oxygène dans le n₂SOIT₃ que dans le n₂Ou, et 5 fois plus d'oxygène dans le n₂SOIT₅ que dans le n₂SOIT. Encore une fois, nous avons de petits nombres entiers, allant de 1 à 5.

Limites

La loi des proportions multiples n'est pas toujours accomplie. Par exemple, les masses molaires ou les poids atomiques des éléments ne sont pas des figures entières, mais a de nombreuses décimales. Cela modifie complètement les relations calculées, qui cessent d'être simples.

De même, la loi n'est pas remplie pour les composés lourds, comme certains hydrocarbures. Par exemple, l'Undecano, C_onzeH₂₄, a 1.0083 ou 121/120 fois plus d'hydrogène que le doyen, c_dixH₂₂, dont la relation est composée de 121 et 120, qui dépasse la douzaine; Ce ne sont pas de petits nombres entiers.

Et enfin, la loi échoue avec des composés non stoichiométriques, comme avec de nombreux oxydes et sulfures.

conclusion

La loi sur les proportions multiples stipule que lorsque deux éléments forment plus d'un composé, les différentes masses d'un élément qui se combinent avec la même masse de l'autre élément sont dans une proportion d'un petit nombre.

Les références

1. Whitten, Davis, Peck & Stanley. (2008). Chimie. (8e Ed.). Cengage Learning.
2. Wikipédia. (2020). Loi des proportions multiples. Récupéré de: dans.Wikipédia.org
3. Les éditeurs d'Enyclopaedia Britannica. (2020). Loi des proportions multiples. Récupéré de: Britannica.com
4. Chimie. (4 juin 2019). Loi des proportions multiples par Dalton. Récupéré de: Chemistrygod.com
5. Garcia Nissa. (2020). Loi des proportions multiples: définition et exemple. Étude. Récupéré de: étudier.com