Ampère Formula and Equations Law, démonstration, exercices

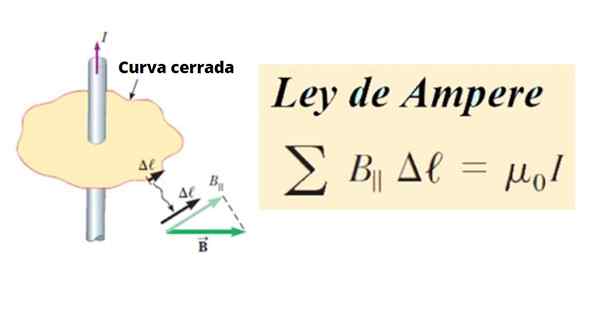
La Loi d'ampères indique que la circulation du vecteur d'induction magnétique B Il est proportionnel à l'intensité et au courant qui coule de même.

À son tour la circulation de B C'est la somme de tous les produits entre le composant tangentiel b_║ et la longueur d'un petit segment Δℓ d'une courbe fermée C, Autour d'un circuit. En termes mathématiques, il est écrit comme ceci:

∑ B_║ .Δℓ ∝ Toi

Figure 1. Définition de la loi Ampère. Source: Serow, R. Physique du collège.

En tant que ligne ou courbe arbitraire, elle peut être divisée en petits segments Δℓ, Et ceux-ci peuvent à leur tour être infinitésimaux, alors ils sont appelés Dℓ.

Dans ce cas, la somme devient une ligne intégrale du produit scalaire entre les vecteurs B et ds. Ce produit contient le composant tangentiel de B, qui est B cosθ, où θ est l'angle entre les vecteurs:

Le petit cercle qui traverse l'intégrale signifie que l'intégration est effectuée sur une trajectoire fermée C, qui dans ce cas implique le courant qui traverse la section transversale du conducteur.

La constante de proportionnalité nécessaire pour établir l'égalité est μ_soit, Perméabilité sous vide. De cette façon, la loi d'Ampère reste:

La loi d'Ampère nous dit que l'intégrale de la ligne ∫_C B ∙ Ds Il vaut exactement μ_soitMoi, mais il ne nous offre pas les détails sur la façon dont le champ magnétique est orienté B Concernant la courbe C à chaque point, ou sur la façon de calculer l'intégrale. Il nous dit seulement que le résultat de la même est toujours μ_soitToi.

[TOC]

Démonstration de la loi d'Ampère

La loi d'Ampère est vérifiée en vérification expérimentalement le champ magnétique produit par un très long conducteur rectiligne. Avant de résoudre le problème, deux cas d'intérêt particulier dans l'équation précédente doivent être mis en évidence:

Il peut vous servir: corps lumineux: caractéristiques et comment elles génèrent leur propre lumière

-Le premier est quand B et ds Ils sont parallèles, ce qui signifie que B est tangentiel à c. Alors l'angle entre les deux vecteurs est de 0º et le produit scalaire est simplement le produit des amplitudes B.ds.

-La seconde se produit si B et ds Ils sont perpendiculaires, auquel cas le produit scalaire est 0, car l'angle entre les vecteurs est de 90 °, dont le cosinus est 0.

Un autre détail important est le choix de la courbe C sur laquelle la circulation sur le terrain est évaluée. La loi d'Ampère ne spécifie pas ce qu'elle peut être, mais elle doit envelopper la distribution actuelle. Il ne dit pas non plus comment parcourir la courbe et il y a deux possibilités pour cela.

La solution consiste à attribuer des panneaux en fonction de la règle du pouce droit. Les quatre doigts sont incurvés dans la direction dans laquelle vous souhaitez intégrer, ce sera généralement le même sur le terrain B circule. Si le courant pointe dans la direction du pouce droit, un panneau est attribué et sinon, signe -.

Cela s'applique lorsqu'il y a une distribution avec plusieurs courants, certains peuvent être positifs et autres négatifs. La somme algébrique est ce que nous allons placer dans la loi de l'ampère, qui est généralement nommée Courant infirmier (Pour la courbe c).

Champ magnétique de la rectiligne et du fil infini

La figure 2 montre un fil qui transporte un courant et hors de l'avion. La règle du pouce droit garantit que B Il circule dans la direction opposée, décrivant les circonférences comme le montrent les flèches rouges.

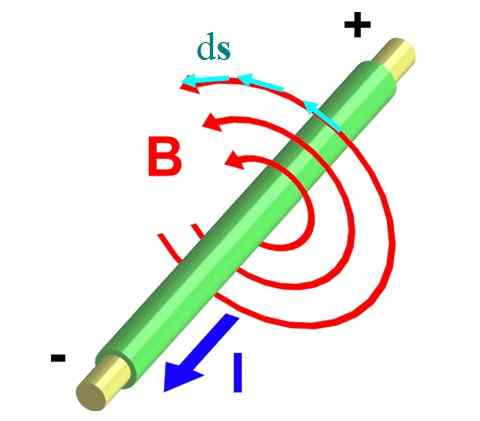Figure 2.- Champ magnétique d'un fil infini. Source: Wikimedia Commons.

Prenons l'un d'eux, dont le rayon est r. Nous le divisez en petits segments différentiels Ds, représenté au moyen de vecteurs bleus. Les deux vecteurs, B et ds, Ils sont parallèles à chaque point de la circonférence, et de cette façon l'intégrale ∫_C B ∙ Ds Il se transforme en:

Peut vous servir: courant direct

∫_C Bds

C'est parce que, comme nous l'avons déjà dit, le produit scalaire B ∙ Ds  C'est le produit des amplitudes des vecteurs par le cosinus 0º. Le résultat de l'intégrale est connu grâce à la loi d'Ampère, donc nous écrivons:

∫_C Bds = μ_soitToi

Étant donné que l'ampleur du champ est constante sur toute la trajectoire, elle laisse l'intégrale:

B ∫_C Ds = μ_soitToi

L'intégrale ∫_C DS représente la somme de tous les segments infinitésimaux qui composent la circonférence radio r, Équivalent à sa longueur, le produit de son rayon par 2π:

B.2πr = μ_soitToi

Et à partir de là, nous constatons que l'ampleur de B est:

B = μ_soitI / 2πr

Il est nécessaire de souligner que même si la trajectoire sélectionnée (ou circuit ampérien) Non circulaire, le résultat de l'intégrale continue d'être μ_soitJe, cependant ∫_C B ∙ Ds Ce ne serait plus b.2πr.

C'est pourquoi l'utilité de la loi d'Ampère pour déterminer le champ magnétique réside dans le choix des distributions avec une symétrie élevée, de sorte que l'intégrale est facile à évaluer. Les trajectoires circulaires et rectilignes répondent à cette exigence.

Exercices résolus

- Exercice 1

Considérez les courbes A, B, C et D montrées sur la figure 3. Ils enveloppent trois courants, deux qui quittent l'avion, symbolisés par un point ( . ), dont les intensités sont 1 a et 5 a, et un courant qui entre dans le plan, qui est indiqué avec une croix et dont l'ampleur est 2 A.

Trouvez le courant enfermé par chaque courbe.

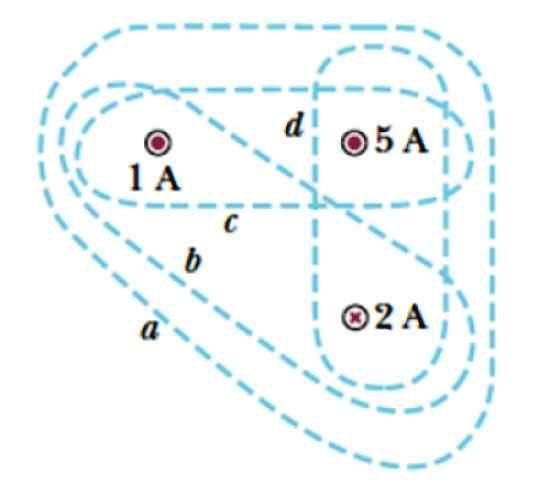figure 3. Plusieurs courbes pour appliquer la loi d'ampère. Source: Serow, R. Physique du collège.

Solution

Les courants qui quittent le papier se voient attribuer un signe +. Selon ce:

Il peut vous servir: vagues superficielles: caractéristiques, types et exemples

Courbe un

Enferme les trois courants, donc le courant fermé est + 1 a + 5 a - 2 a = 4 a.

Courbe b

Seuls les courants de 1 a y - 2 a sont à l'intérieur de cette courbe, donc le courant fermé est de - 2 a.

Courbe c

Contient les courants sortants 1 et 5 a, donc le courant fermé est 6 A.

Incurvé

Les courants à l'intérieur sont +5 a et - 2 a, puis enferme un courant net de 3 à.

- Exercice 2

Calculez l'amplitude du champ magnétique produit par un très long fil rectiligne.

Solution

Selon la loi d'Ampère, le champ de fil est donné par:

B = μ_soitI / 2πr = (4π x 10^-7 x 1/2π x 1) t = 2 x 10^-7 T.

Les références

1. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 6. Électromagnétisme. Édité par Douglas Figueroa (USB).
2. Chevalier, r.  2017. Physique pour les scientifiques et l'ingénierie: une approche stratégique.  Pearson.
3. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. 2ieme volume.
4. SERAY, R. 2009. Physique du collège. Cengage Learning.
5. Tipler, P. (2006) Physique de science et de technologie. 5e ed. 2ieme volume. Éditorial Revered.