Interpolation linéaire

Nous expliquons quelle est l'interpoation linéaire, ses formules, comment en faire un, avec des exemples et des exercices résolus

Qu'est-ce que l'interpolation linéaire?

La Interpolation linéaire Il consiste à estimer l'emplacement d'un point dans un intervalle numérique, en supposant que les valeurs extrêmes dudit intervalle sont unies par une ligne. Connu de l'équation de cette ligne, il est possible de localiser le point inconnu.

L'idée est schématique dans la figure suivante, qui montre une approche du graphique d'une fonction entre les points A et B. En supposant que ces points sont proches, il est possible d'approximer la courbe qui les unit à travers une ligne et de trouver ainsi les points intermédiaires.

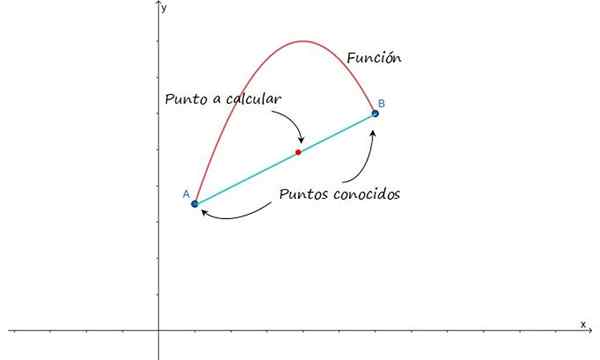Figure 1.- Pour faire une interpolation linéaire entre les points A et B, il faut supposer qu'ils sont unis par une ligne . Source: F. Zapata.

Vous pouvez également approximer la courbe qui rejoint les points donnés au moyen d'une fonction quadratique ou d'un autre polynôme. Cependant, la ligne a l'avantage de sa simplicité mathématique, il est donc facile à gérer, bien que ce soit l'interpolation la plus simple de toutes, il est possible que le résultat ne soit pas aussi précis que celui obtenu en utilisant d'autres fonctions.

Formules

Il y a deux points de coordonnées [x_soit, f (x_soit)] et [x₁, f (x₁)] parmi lesquels est le point [x, g (x)], dont les coordonnées sont souhaitées à savoir.

La première étape consiste à rejoindre les points connus à travers un segment de ligne, sur lequel sont trouvés les coordonnées du point un calcul.

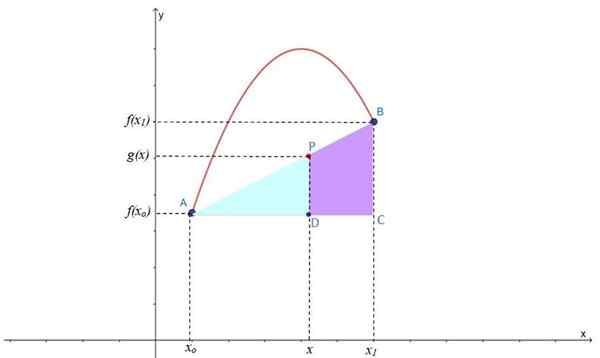Figure 2.- Interpolation linéaire pour trouver le point P sur la ligne d'interpoching g (x), située entre les points A et B de F (x). Source: F. Zapata.

Comme vous pouvez le voir, deux rectangles se forment: ABC et APD, qui ont également un angle aigu en commun, donc ce sont des triangles similaires, auxquels le théorème des thales peut être appliqué:

Il peut vous servir: géométrie analytique

Remplacement de la mesure des segments en fonction du graphique, la relation suivante est obtenue:

De là, nous procédons à effacer G (x):

 Appel:

F₁(X₁) = y₁ ; F_soit(X_soit) = y_soit ; g (x) = y

L'équation supérieure est transformée en:

Marge d'erreur

Lorsqu'une fonction s'approche avec cette méthode, le niveau d'erreur est donné par la valeur absolue de la différence entre la fonction f (x) et la ligne d'interpolation g (x):

Erreur = │f (x) - g (x) │

Comment faire une interpolation linéaire?

La réalisation d'une interpolation linéaire est très simple, il vous suffit de suivre ces étapes:

Étape 1

Déterminez le point inconnu P (x, y).

Étape 2

Établir les deux points qui limitent l'intervalle où la valeur à calculer est située, c'est-à-dire les points (x x_soit,et_soit) et (x₁, et₁).

Étape 3

Remplacez toutes les valeurs de l'équation:

Et calculer le résultat.

Exemples d'interpolation linéaire

Exemple 1

Vous souhaitez trouver la valeur approximative de LN 3 à l'interpolation linéaire, compte tenu des valeurs suivantes:

ln 2 = 0.693147 et ln 4 = 1.386294

Comparez le résultat avec la valeur de Ln 3 obtenue via une calculatrice et déterminez la marge engagée.

• Étape 1

Pour trouver la valeur approximative de Ln 3, vous devez procéder à la suite: Premièrement, l'inconnu est établi, qui est y = ln 3, à côté de sa valeur correspondante de «x»: x = 3. C'est le point que vous souhaitez calculer: (3, ln 3).

• Étape 2

Ensuite, vous devez établir les points limites de l'intervalle avec les valeurs connues. Il est demandé de le faire avec les deux prochains points:

• Limite inférieure: [x_soit = 2; et_soit = ln 2 = 0.693147]
• Limite supérieure: [x₁ = 4; et₁ = ln 4 = 1.386294]

• Étape 3

Les valeurs déterminées aux étapes 1 et 2 sont soigneusement remplacées dans l'équation pour générer le résultat de l'approche de Ln 3:

Peut vous servir: combien de solutions une équation quadratique a-t-elle?

La valeur réelle de Ln 3 obtenue par calculatrice est:

ln 3 = 1.098612

Et la marge d'erreur est:

Erreur = │1.098612 - 1.03971 │ = 0.059

Le pourcentage d'erreur de l'interpolation est calculé en divisant l'erreur entre la valeur réelle de LN3 et en multipliant par 100%:

Pourcentage d'erreur = (erreur / valeur réelle) × 100 = (0.059/1.098612) × 100% = 5.4%

Exemple 2

Vous souhaitez maintenant trouver la valeur approximative de LN 3 par interpolation linéaire, connu ces deux valeurs:

ln 2.5 = 0.916291 et ln 3.5 = 1.252763

Déterminez également l'erreur correspondante et comparez avec les résultats de l'exemple précédent.

• Étape 1

Encore une fois, le point inconnu est:

y = ln 3, x = 3

• Étape 2

• Limite inférieure: [x_soit = 2.5; et_soit = Y_soit = ln 2.5 = 0.916291]
• Limite supérieure: [x₁ = 3.5; et₁ = ln 3.5 = 1.252763]

• Étape 3

Examiner la valeur offerte par la calculatrice:

ln 3 = 1.098612

Le niveau d'erreur est déterminé dans ce cas, ce qui en résulte:

Erreur = │1.098612 - 1.084527 │ = 0.014

Le pourcentage d'erreur dans ce cas est ≈ 1.3%. En comparaison avec le niveau d'erreur de l'exemple 1, la nouvelle valeur est plus précise, car l'intervalle choisi à interpolaire est plus bas.

Exercices résolus

Exercice 1

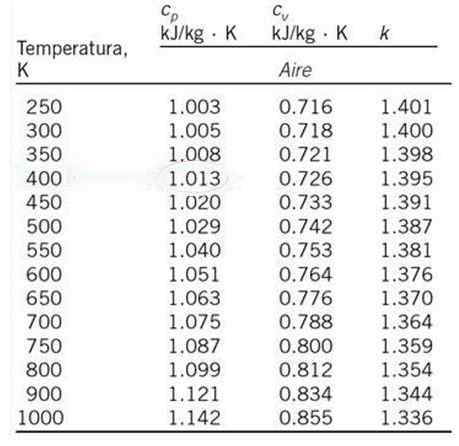
Calculez, par interpolation linéaire, la chaleur spécifique de l'air à pression constante C_p  et température de 530 K, à partir du tableau des valeurs indiquées ci-dessous.

• Solution

Dans la résolution de nombreux problèmes, il est courant que la valeur recherchée n'apparaît pas exactement comme souhaité dans le tableau des valeurs à portée de main. Une alternative consiste à choisir la valeur la plus proche de la plus proche de celle souhaitée, mais plusieurs fois une interpolation linéaire est suffisante pour trouver une bien meilleure approche.

Peut vous servir: signes de regroupement

La valeur de c_p Un 530 K n'apparaît pas dans la table attachée, mais une interpolation linéaire peut être faite avec les chaleurs spécifiques respectives à 500 K et 550 K, qui sont les températures les plus proches de 530 K et dont les chaleurs spécifiques apparaissent dans le tableau montré.

Les chaleurs de chaleur spécifiques respectives pour ces températures sont:

T_soit = 500 K; c_pote = 1.029 kJ / kg ∙ k

T₁ = 550 K; c_P1 = 1.040 kJ / kg ∙ k

Et l'inconnu est le point (500k, C_p)

Remplacement dans la formule de l'interpolation linéaire donnée ci-dessus, avec t sur la scène de la variable "x" et c_p Au lieu de "Y", vous avez:

Exercice 2

La charge appliquée à un ressort (en kilopondios) produit les allonges suivants (en millimètres) selon le tableau indiqué:

Calculer l'allongement lorsque la charge est 12.6 kp.

• Solution

Soit et la valeur de l'allongement recherché lorsque la charge est c = 12.6 kp. Le point inconnu est (12.6, y), qui fait partie des points:

C_soit = 10 kp; et_soit = 105 mm

C₁ = 15 kp; et₁ = 172 mm

Il reste seulement pour remplacer les valeurs de l'équation:

Exercice proposé

Calculez la chaleur spécifique à un volume constant pour une température de 727 K, en utilisant une interpolation linéaire et le tableau des titres de l'exercice résolu 1.

Les références

1. Rafa Vilchez Academy. Comment effectuer une interpolation linéaire. Récupéré de: Academiraafavilchez.com
2. Chapra, s. 2007. Méthodes numériques pour les ingénieurs. 5e. Édition. McGraw Hill.
3. Académie Khan. Mathématiques de l'interpolation linéaire. Récupéré de: Khanacademy.org.
4. La vie éducative. Formule d'interpolation linéaire. Récupéré de: theDeducationLife.com
5. X-ingénieur. Interpolation et extrapolation linéaires avec calculatrice. Récupéré de: x-ingénieur.org.