Identités trigonométriques (exemples et exercices)

Le identités trigonométriques Ce sont des relations entre des raisons trigonométriques, qui sont vraies pour toute valeur de la variable. Par exemple:

Tan θ = sin θ / cos θ

Il s'agit d'une identité trigonométrique qui relie trois raisons de l'angle θ, de la tangente, du sein et du cosinus dudit angle.

Figure 1. Certaines identités trigonométriques largement utilisées dans le calcul. Source: F. Zapata.

Cette identité est vraie pour toute valeur, sauf celles qui font 0 le dénominateur. Le cos θ est 0 pour θ = ± π / 2, ± 3π / 2, ± 5π / 2… Un autre exemple d'identité trigonométrique est:

péché x . Sec x . Ctg x = 1

[TOC]

Manifestation

Il existe deux façons de base de démontrer qu'une identité trigonométrique est vraie:

1- Transformer l'un des membres de l'égalité en l'autre, à travers des manipulations algébriques pratiques.

2- Développez les deux membres de l'égalité séparément, jusqu'à ce que les expressions finales respectives de chacun soient exactement les mêmes.

Dans l'identité proposée, nous allons transformer le côté gauche de l'égalité, pour laquelle nous exprimons CTG X et Sec x en termes de sein et de cosinus comme suit:

Ctg x = cos x / sen x

Sec x = 1 / cos x

Nous remplaçons cette expression sur le côté gauche de l'identité et simplifions:

péché x . (1 / cos x). (cos x / sen x) = (sin x. cos x / cos x . sin x) = 1

Et la véracité de l'identité est déjà prouvée.

Types d'identités trigonométriques

Il existe plusieurs types d'identités trigonométriques. Ensuite, nous décrirons brièvement les principaux:

- Identités trigonométriques fondamentales

Nous distinguons deux types d'identités fondamentales:

I) Ceux qui sont exprimés par les raisons fondamentales, le cosinus et la tangente:

• Sec x = 1 / cos x
• Dommage x / 1 / sin x
• Ctg x = 1 / tg x
• Tg x = sin x / cos x
• Ctg x = cos x / sen x

I) Ceux dérivés de la parité. Nous savons à travers son graphique que Sen X est une fonction étrange, ce qui signifie que:

Peut vous servir: 60 diviseurs

sin (-x) = - sin x

Pour sa part, Cos X est donc un couple:

cos (-x) = cos x

Ensuite:

tg (-x) = sen (-x) / cos (-x) = -sen x / cos x

De la même forme:

• cotg (-x) = -ctg x
• sec (-x) = sec x
• dommage (-x) = - dommage x

- Identités pythagoriennes

Ce sont ceux obtenus de l'application du théorème de Pythagore au triangle rectangle des chats A et B et Hypotenusa C. Voyons:

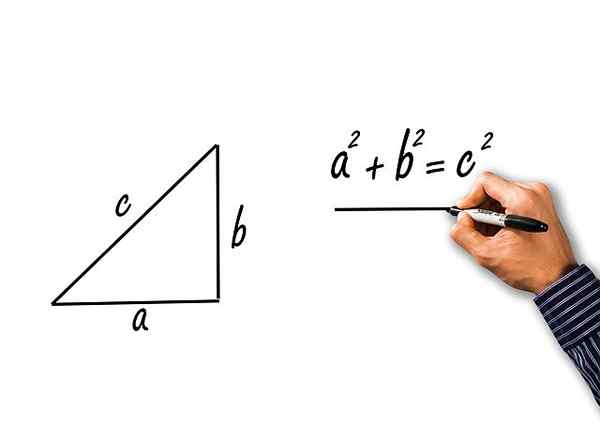Figure 2.- Du théorème de Pythagore, les trois identités trigonométriques pythagoriennes sont obtenues. Source: Pixabay.

Le théorème de Pythagore déclare que:

c² = A² + b²

Tout diviser entre c²:

c² / c² = (a² / c²) + (B² / c²)

Le terme de gauche est 1 et se rappelant que le sinus et le cosinus de l'angle aigu α sont définis comme:

sin α = a / c

cos α = b / c

Résultat:

1 = (sin α)² + (cos α)²

Cette identité est connue sous le nom identité fondamentale.

La procédure peut être effectuée en divisant entre² et B², qui donne naissance à deux autres identités:

Seconde² α = 1 + tg² α

har² α = 1 + ctg² α

- Formules pour le cosinus et le sein de la somme / soustraction des angles

Les principales identités trigonométriques pour le cosinus, le sein et la tangente de la somme et de la soustraction sont les suivantes:

Démonstration sénable (α + β) et COS (α + β)

Ces identités peuvent être démontrées géométriquement ou également à travers la formule Euler:

et^iα = cos α + i sin α

Regardons ce qui arrive à la formule lors du remplacement de la somme de deux angles α et β:

et^{I (α +β)} = cos (α + β) + i sin (α + β)

Cette expression est complexe, sa partie réelle est COS (α + β) et sa partie imaginaire est i sin (α + β). Nous gardons ce résultat pour l'utiliser plus tard et nous concentrons sur le développement de la partie exponentielle:

et^{I (α +β)} = e^iα ⋅ e^iβ = (cos α + i sin α) . (cos β + i sin β) =

Peut vous servir: prisme hexagonal

= cos α⋅cos β + cos α⋅i sen β + i⋅ssen α cos β - sen α⋅sen β

La partie réelle de cette expression est celle qui n'est pas multipliée par l'unité imaginaire "i":

cos α⋅cos β - sen α. Sen β

La partie imaginaire est donc:

I (cos α⋅sen β + sen α⋅cos β)

Pour que deux expressions complexes soient les mêmes, la partie réelle de l'une doit être égale à la partie réelle de l'autre. Il en va de même pour les parties imaginaires.

Nous prenons les résultats sauvés et le comparons à cela:

cos α. cos β - sen α. sin β = cos (α + β)

i (cos α⋅sen β + sen α⋅cos β) = i sin (α + β)

sin (α + β) = (cos α. sin β + sen α⋅cos β)

- Formules pour le double angle

Dans les formules précédentes, nous prenons β = α et nous développons:

sin (α + α) = sen 2 α = sen α⋅cos α + cos α. sin α = 2⋅ sin α ⋅ cos α

cos (α + α) = cos 2 α = cos α⋅cos α - sen α⋅sen α = cos² α - sen ² α

Tg (α + α) = Tg 2 α = [Tg α + Tg α] / [1- Tg α⋅tg α] = 2tg α / 1- tg² α

Si dans la deuxième expression, les cos sont remplacés² α = 1 - Sen² α est obtenu:

cos 2 α = cos² α- (1- cos² α) = 2 cos² α -1

- Formules à moitié en angle

Dans cette dernière expression, nous remplaçons α par α / 2, ce qui suit reste:

cos α = 2 cos ²(α / 2) -1

Clairière:

Exercices résolus

- Exercice 1

Montre CA:

Solution

Nous allons travailler algébriquement le terme gauche pour qu'il ressemble à droite. Comme dans le bon terme apparaît Sen X, la première étape consiste à exprimer Cos²X En termes de sen x pour que tout soit en termes de même raison trigonométrique:

Il peut vous servir: une fraction équivalente à 3/5 (solution et explication)

Alors 1 - Sen est le facteur² X pour être une différence de carrés parfaits. Pour ce faire, il s'éclaircit de l'identité fondamentale:

cos²X = 1 - Sen² X

1 - Sen² x = (1- sin x) (1 + senx)

Et la factorisation de l'expression d'origine est remplacée:

Le terme (1- Senx) est simplifié et une égalité reste:

1 + Sen x = 1 + Senx

- Exercice 2

Résolvez l'équation trigonométrique suivante et donnez la solution pour les valeurs entre 0 et 360º:

Tg x + sec² x = 3

Solution

Dans le terme de gauche, il y a deux raisons trigonométriques, vous devez donc tout réduire à un, afin de pouvoir effacer l'inconnu. Le terme sec² X est exprimé par l'une des identités pythagoriennes:

Seconde² α = 1 + tg² α

En remplaçant l'équation:

Tg x + 1 + tg² x = 3

Réorganiser les termes:

Tg² x + tg x + 1 = 3

Cette équation est résolue en modifiant la variable:

tg x = u

ou² + U + 1 - 3 = 0 → U² + U - 2 = 0

Cette équation du deuxième degré est facilement résolue par factorisation:

(U +2) (U-1) = 0

Par conséquent₁ = -2 et u₂ = 1, équivalent à:

Tg x₁ = -2

Tg x₂ = 1

Finalement:

X₁ = arctg (-2) = 296.6e

X₂  = arctg (1) = 45º

Les références

1. Carena, m. 2019. Manuel des mathématiques de préunité. Université nationale de la côte.
2. Figuera, J. 1999. Mathématiques. 1er. Diversifié. Éditions collégiales bolivariennes.
3. Hoffman, J. Sélection de problèmes de mathématiques. Volume 4.
4. Jiménez, R. 2008. Algèbre. Prentice Hall.
5. Wikipédia. Identités et formules de trigonométrie. Récupéré de: est.Wikipédia.org.
6. Zapata, f. 4 façons de résoudre une équation du deuxième degré. Récupéré de: Francesphysics.Blogspot.com.
7. Zill, D. 1984. Algèbre et trigonométrie. McGraw Hill.