Définition hypercubo, dimensions, coordonnées, dépliée

UN hypercubo est un cube de dimension n. Le cas particulier de la dimension hypercubo est appelé TesterACT. Un hypercubo ou n-cubo se compose de segments droits, toutes les mêmes longueurs qui sont orthogonales dans leurs sommets.

Les êtres humains perçoivent l'espace à trois dimensions: large, haut et profondeur, mais il n'est pas possible pour nous de visualiser une hypercubo de dimension supérieure à 3. 

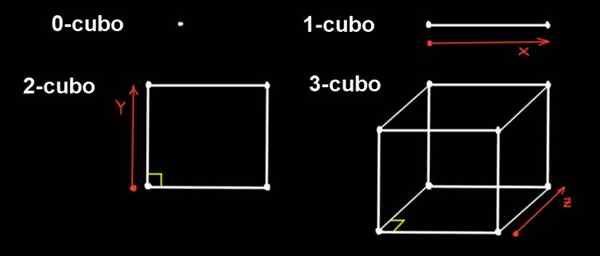
Figure 1. Un 0-cubo est un point, si ce point s'étend dans une direction une distance d'une manière à 1-cubo, si ce 1-cubo s'étend sur une distance dans la direction orthogonale, il y a un 2-cubo (des côtés à x a), Si le 2-cubo s'étend sur une distance à la direction orthogonale, il y a un 3-cubo. Source: F. Zapata.

Nous pouvons faire des projections dans l'espace à trois dimensions pour le représenter, similaire à la façon dont nous projetons un cube sur un avion pour le représenter.

En dimension 0, la seule figure est le point, donc un 0-cubo est un point. Un 1-cubo est un segment droit, qui est formé en déplaçant un point à une distance à une distance à.

Pour sa partie, un 2-cubo est un carré. Il est construit en déplaçant le 1-cubo (le segment long a) dans la direction et, qui est orthogonal à l'adresse x, une distance à.

Le 3-cubo est le cube commun. Il est construit à partir du carré déplaçant la même chose dans la troisième direction (z), qui est orthogonale aux directions x et y, une distance pour.

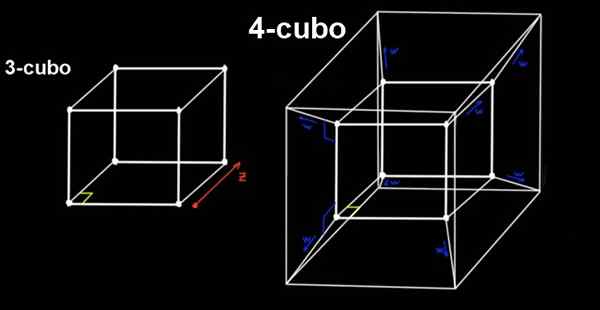Figure 2. Un 4-cubo (Testeract) est l'extension d'un 3-cubo dans la direction orthogonale aux trois adresses spatiales conventionnelles. Source: F. Zapata.

Le 4-Cubo est l'essai, qui est construit à partir d'un 3-cubo déplaçant le même orthogonalement, une distance pour, vers une quatrième dimension (ou quatrième direction), que nous ne pouvons pas percevoir.

Un déclencheur a tous ses angles droits, il a 16 sommets et tous ses bords (18 au total) ont la même longueur pour.

Si la longueur des bords d'un n-cubo ou hypercubo de dimension n est 1, alors c'est une unité hypercubo, dans laquelle les plus longues mesures diagonales √n.

Peut vous servir: programmation linéaire: à quoi sert, modèles, restrictions, applicationsfigure 3. Un n-cubo est obtenu à partir d'un (n-1) -cubo l'étendant orthogonalement dans la dimension suivante. Source: Wikimedia Commons.

[TOC]

Quelles sont les dimensions?

Les dimensions sont les degrés de liberté, ou les directions possibles dans lesquelles un objet peut se déplacer.

Dans la dimension 0, il n'y a aucune possibilité de se déplacer et le seul objet géométrique possible est le point.

Une dimension dans l'espace euclidien est représentée par une ligne ou un axe orienté qui définit cette dimension, appelée l'axe x. La séparation entre deux points A et B est la distance euclidienne:

D = √ [(x_pour - X_b)²]]. 

En deux dimensions, l'espace est représenté par deux lignes orientées orthogonales les unes avec les autres, appelées x et axe.

La position de n'importe quel point dans cet espace à deux dimensions est donnée par sa paire de coordonnées cartésiennes (x, y) et la distance entre deux points A et B tout sera:

D = √ [(x_pour - X_b)² + (et_pour - et_b)²]]

Parce que c'est un espace où la géométrie euclide est remplie.

L'espace à trois dimensions

L'espace à trois dimensions est l'espace dans lequel nous nous déplaçons. Il a trois directions: largeur, élevée et profondeur.

Dans une pièce vide, les coins perpendiculaires les uns entre eux donnent ces trois directions et à chacun, nous pouvons associer un axe: x, y, z.

Cet espace est également euclidien et la distance entre deux points A et B est calculée comme suit:

D = √ [(x_pour - X_b)² + (et_pour - et_b)² + (Z_pour - z_b)²]]

Les êtres humains ne peuvent pas percevoir plus de trois dimensions spatiales (ou euclideas).

Cependant, du point de vue strictement mathématique, c'est possible.

Dans cet espace, un point a des coordonnées: (x1, x2, x3, ..., xn) et la distance entre deux points est: 

D = √ [(x_1er - X_{1 b})² + (X_2e - X_2B)² +... + (x_{n / A} - X_NB)²]].

Peut vous servir: Distribution hypergéométrique: formules, équations, modèle

La quatrième dimension et le temps

En effet, en théorie de la relativité, le temps est traité comme une dimension de plus et une coordonnée est associée.

Mais il faut préciser que cette coordonnée associée au temps est un numéro imaginaire. Par conséquent, la séparation de deux points ou événements dans l'espace-temps n'est pas Euclidiana, mais suit la métrique de Lorentz.

Un hypercubo à quatre dimensions (le déclencheur) ne vit pas dans l'espace-temps, appartient à une hyper-espace euclidéal à quatre dimensions. 

Figure 4. Projection 3D d'une hypercubo à quatre dimensions en rotation simple autour d'un avion qui divise la figure avant à gauche, à droite à droite et de haut en bas. Source: Wikimedia Commons.

Les coordonnées d'un hypercubo

Les coordonnées des sommets d'un N-cubo centré sur l'origine sont obtenues en faisant toutes les permutations possibles de l'expression suivante:

(A / 2) (± 1, ± 1, ± 1, .. ., ± 1)

Où a est la longueur du bord.

-Il volume À partir d'un bord du bord a est: (a / 2)ⁿ (2ⁿ) = aⁿ.

-La la plus longue diagonale C'est la distance entre les sommets opposés.

-Voici Vertices opposées dans un carré: (-1, -1) et (+1, +1).

-Et dans un cube: (-1, -1, -1) et (+1, +1, +1). 

-La la plus longue diagonale d'une mesure n-cubo: 

D = √ [1 - (-1))² +… + (1 - (-1))²] = √ [n 2²] = 2√n

Dans ce cas, on a supposé que le côté est a = 2. Pour un côté n-cubo à quiconque restera:

d = a√n.

-Un essai a chacun de ses 16 sommets connectés à quatre bords. La figure suivante montre comment les sommets sont connectés dans un déclencheur.

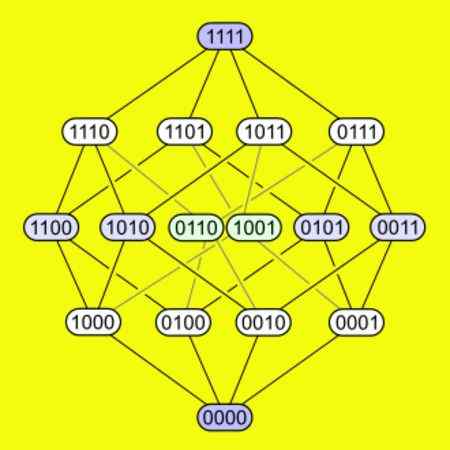Figure 5. Les 16 sommets d'un hypercubo à quatre dimensions sont affichés et comment ils relient la même chose. Source: Wikimedia Commons.

Déplié d'un hypercubo

Un chiffre géométrique ordinaire, par exemple un polyèdre, peut être déplié dans plusieurs chiffres de dimensionnalité plus bas.

Dans le cas d'un 2-cubo (un carré) peut être déplié en quatre segments, c'est-à-dire quatre 1-cubo.

Il peut vous servir: Distribution de Poisson: formules, équations, modèle, propriétés

De même, un 3-cubo peut être déplié en six 2-cubo.

Figure 6. Un n-cubo peut être déplié dans plusieurs (n-1) -cubos. Source: Wikimedia Commons.

Un 4-cubo (Testeract) peut être déplié en huit 3-cubo.

L'animation suivante montre le déploiement d'un tripe.

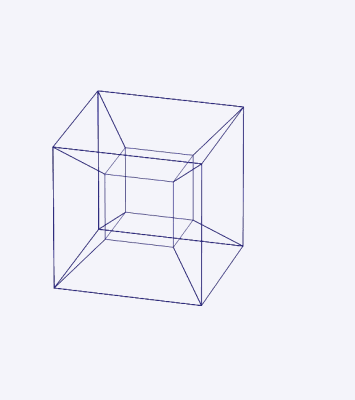Figure 7. Une hypercubo à 4 dimensions peut être dépliée dans huit cubes à trois dimensions. Source: Wikimedia Commons. Figure 8. Projection à trois dimensions d'un hypercubo à quatre dimensions faisant une double rotation autour de deux plans orthogonaux. Source: Wikimedia Commons.

Les références

1. Culture scientifique. Hypercubo, visualisant la quatrième dimension. Récupéré de: Culturacientifica.com
2. Epsilones. Hypercubo ou Tesseract tétradimensionnel. Récupéré de: epsilones.com
3. Perez R, Aguilera A. Une méthode pour obtenir un essai à partir du développement d'un hypercub (4d). Récupéré de: Researchgate.filet
4. Wikilibros. Mathématiques, polyèdres, hypercubes. Récupéré de: est.Wikibooks.org
5. Wikipédia.  Hypercube. Récupéré de: dans.Wikipédia.com
6. Wikipédia. Tisseract. Récupéré de: dans.Wikipédia.com