Degrés de liberté Comment les calculer, les types, les exemples

Les degrés de liberté Dans les statistiques sont le nombre de composants indépendants d'un vecteur aléatoire. Si le vecteur a n composants et il y a p équations linéaires qui relient ses composants, puis le degré de liberté C'est n-p.

Le concept de degrés de liberté Il apparaît également dans la mécanique théorique, où en mode brut, ils équivaut à la dimension de l'espace où se déplace la particule, à l'exception du nombre de ligatures.

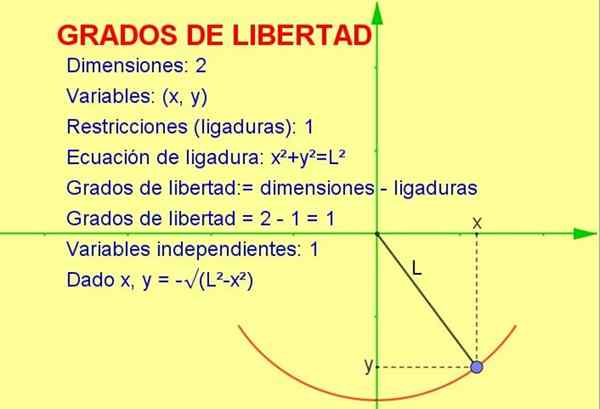
Figure 1. Un pendule se déplace en deux dimensions, mais il n'a qu'un degré de liberté car il est obligé de se déplacer dans un rayon arc l. Source: F. Zapata.

Cet article discutera du concept de degrés de liberté appliqués aux statistiques, mais un exemple mécanique est plus facile à visualiser de manière géométrique.

[TOC]

Types de degrés de liberté

Selon le contexte dans lequel il est appliqué, la façon de calculer le nombre de degrés de liberté peut varier, mais l'idée sous-jacente est toujours la même: dimensions totales moins de restrictions.

Dans un cas mécanique

Considérez une particule qui oscille liée à une corde (un pendule) qui se déplace dans le plan vertical X-Y (2 dimensions). Cependant, la particule est obligée de se déplacer sur la circonférence du rayon égal à la longueur de la corde.

Comme la particule ne peut que se déplacer sur cette courbe, le nombre de degrés de liberté C'est 1. Cela peut être visualisé dans la figure 1.

La façon de calculer le nombre de degrés de liberté est de faire la différence dans le nombre de dimensions, sauf le nombre de restrictions:

Degrés de liberté: = 2 (dimensions) - 1 (ligature) = 1

Une autre explication qui nous permet d'atteindre le résultat est la suivante:

-Nous savons que la position à deux dimensions est représentée par un point de coordonnée (x, y).

-Mais comme le point doit remplir l'équation de circonférence (x² + et² = L²) Pour une valeur donnée de variable x, la variable et est déterminée par cette équation ou restriction.

De cette façon, une seule des variables est indépendante et le système a Un (1) degré de liberté.

Peut vous servir: Probabilité classique: calcul, exemples, exercices résolus

Dans un ensemble de valeurs aléatoires

Pour illustrer ce que le concept signifie supposer le vecteur

X = (x₁, X₂,…, X_n)

Représentant l'échantillon de n Valeurs aléatoires normalement distribuées. Dans ce cas, le vecteur aléatoire X a n composants indépendants et donc il est dit que X a n degrés de liberté.

Construisons le vecteur maintenant r des déchets

r = (x₁ - , X₂ - ,.. ., X_n - )

Où il représente la moyenne de l'échantillon, qui est calculé comme suit:

= (x₁ + X₂ +.. .+ X_n) / n

Puis la somme

(X₁ - ) + (x₂ - ) + .. .+(X_n - ) = (x₁ + X₂ +.. .+ X_n) - n = 0

C'est une équation qui représente une restriction (ou ligature) dans les éléments vectoriels r des déchets, puisque si N-1 est connu, les composants vectoriels r, L'équation de restriction détermine le composant inconnu.

Par conséquent, le vecteur r de dimension n avec la restriction:

∑ (x_Toi - ) = 0

A (N - 1) degrés de liberté.

Encore une fois, il est appliqué que le calcul du nombre de degrés de liberté est:

Degrés de liberté: = N (dimensions) - 1 (restrictions) = n -1

Exemples

Variance et degrés de liberté

La variance s² Il est défini comme la moyenne du carré des écarts (ou déchets) de l'échantillon de données:

s² = (r•r) / (N-1)

où r est le vecteur de déchets r = (x1 -, x2 -, .. ., Xn -) et le point épais (•) est l'opérateur de produit scalaire. Alternativement, la formule de variance peut être écrite comme suit:

s² = ∑ (x_Toi - )² / (N-1)

Dans tous les cas, il convient de noter que lors du calcul de la moyenne du carré des déchets, il est divisé par (n-1) et non entre n, car comme discuté dans la section précédente, le nombre de degrés de liberté de la vecteur r est (n-1).

Si pour le calcul de la variance, il était divisé entre n Au lieu de (n-1), le résultat aurait un biais très significatif pour les valeurs de n moins de 50.

Il peut vous servir: géométrie analytique

Dans la littérature apparaît également la formule de la variance avec le diviseur n au lieu de (n-1), en ce qui concerne la variance d'une population.

Mais l'ensemble de la variable aléatoire des déchets, représentée par le vecteur r, Bien qu'il ait une dimension n, il n'a que (N-1) degrés de liberté. Cependant, si le numéro de données est suffisamment grand (n> 500), les deux formules convergent vers le même résultat.

Les calculatrices et les feuilles de calcul offrent les deux versions de la variance et l'écart type (qui est la racine carrée de la variance).

Notre recommandation, compte tenu de l'analyse présentée ici, est de toujours choisir la version avec (n-1) chaque fois qu'il est nécessaire de calculer la variance ou l'écart type, pour éviter les résultats avec un biais.

Dans la distribution de chi carré

Certaines distributions de probabilité dans une variable aléatoire continue dépendent d'un paramètre appelé degré de liberté, C'est le cas de la distribution de Chi Square (χ²).

Le nom dudit paramètre provient juste des degrés de liberté du vecteur aléatoire sous-jacent auquel cette distribution est appliquée.

Supposons qu'il existe des populations G, dont les échantillons de taille N sont prélevés:

X₁ = (x1₁, x1₂,... x1_n)

X2 = (x2₁, x2₂,... x2_n)

.. .

X_J = (xj₁, xj₂,… XJ_n)

.. .

Xg = (xg₁, Xg₂,… Xg_n)

Une population J qui a un écart moyen et standard SJ, Suivez la distribution normale n (, SJ ).

La variable typiquement ou normalisée ZJ_Toi est défini comme:

Zj_Toi = (xj_Toi - ) / SJ.

Et le vecteur Zj Il est défini comme ceci:

Zj = (Zj₁, Zj₂,…, ZJ_Toi,…, ZJ_n) Et suivre la distribution normale typique n (0,1).

Puis la variable:

Q = ((Z1₁ ^ 2 + Z2₁^ 2 +… . + Zg₁^ 2),… ., (Z1_n^ 2 + Z2_n^ 2 +… . + Zg_n^ 2))

Suivez la distribution χ²(g) appelé le Distribution de chi carré avec degré de liberté g.

Dans le contraste d'hypothèse (avec un exemple résolu)

Lorsque vous souhaitez faire un contraste d'hypothèse basé sur un certain ensemble de données aléatoires, il est nécessaire de connaître le nombre de degrés de liberté g Pour pouvoir appliquer le test Chi Square.

Peut vous servir: distribution uniforme continue: caractéristiques, exemples, applications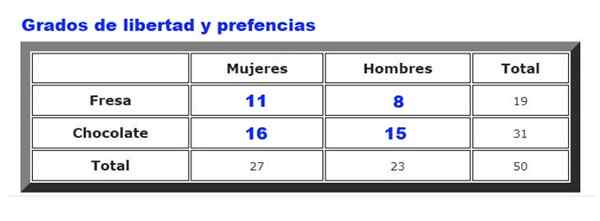 Figure 2. Y a-t-il une relation entre le goût de la crème glacée et le sexe des clients? Source: F. Zapata.

À titre d'exemple, les données recueillies sur les préférences de crème glacée au chocolat ou aux fraises entre hommes et femmes dans un magasin de crème glacée seront analysées. La fréquence avec laquelle les hommes et les femmes choisissent la fraise ou le chocolat, est résumé dans la figure 2.

Premièrement, le tableau de fréquence attendu est calculé, qui est fabriqué en multipliant le Total des lignes pour lui Colonnes totales, divisé par Données totales. Le résultat est illustré dans la figure suivante:

figure 3. Calcul des fréquences attendues basées sur les fréquences observées (valeurs bleues sur la figure 2). Source: F. Zapata.

Ensuite, nous procédons à calculer le CHI Square (à partir des données) par la formule suivante:

χ² = ∑ (f_soit - F_et)² / F_et

Où f_soit sont les fréquences observées (figure 2) et f_et sont les fréquences attendues (figure 3). La somme est dans tous les rangs et colonnes, qui dans notre exemple donnent quatre termes.

Après avoir fait les opérations que vous obtenez:

χ² = 0,2043.

Il est maintenant nécessaire de se comparer avec le carré théorique, qui dépend du nombre de degrés de liberté g.

Dans notre cas, ce nombre est déterminé comme suit:

G = (#Filas - 1) (#Columnas - 1) = (2 - 1) (2 - 1) = 1 * 1 = 1.

Il s'avère que le nombre de degrés de liberté G de cet exemple est 1.

Si vous souhaitez vérifier ou rejeter l'hypothèse nulle (H0: il n'y a pas de corrélation entre la saveur et le sexe) avec un niveau de signification de 1%, le carré théorique est calculé avec le degré de liberté g = 1.

La valeur qui fait que la fréquence accumulée est recherchée (1 - 0.01) = 0.99, c'est 99%. Cette valeur (qui peut être obtenue à partir des tables) est 6.636.

Alors que le chi théorique dépasse le calculé, alors l'hypothèse nulle est vérifiée.

C'est-à-dire qu'avec les données collectées, il n'y a pas de relation entre la saveur des variables et le sexe.

Les références

1. Minitab. Quels sont les degrés de liberté? Récupéré de: Support.Minitab.com.
2. Moore, David. (2009) Statistiques appliquées de base. Éditeur d'Antoni Bosch.
3. Leigh, Jennifer. Comment calculer les degrés de liberté dans les modèles statistiques. Récupéré de: Geniolia.com
4. Wikipédia. Degré de liberté (statistiques). Récupéré de: est.Wikipédia.com
5. Wikipédia. Degré de liberté (physique). Récupéré de: est.Wikipédia.com