Géométrie euclidienne

Nous expliquons quelle est la géométrie euclidienne, son histoire, ses éléments et nous donnons plusieurs exemples

Euclide d'Alexandrie et ses éléments, par Jus de Jusepe de Ribera, à côté, deux lignes non parallèles et une ligne qui les coupe, illustrant le cinquième postulat. Source: Wikimedia Commons.

Qu'est-ce que la géométrie euclidienne?

La Géométrie euclidienne C'est celui qui est régi par les postulats par Euclid de Alejandría, un géomètre grec qui vivait vers 300 pour.C, en l'honneur de lequel cette discipline est nommée, car elle a été la première à la systématiser.

Cette branche des mathématiques étudie les propriétés des lignes, des plans, des angles et des figures géométriques telles que les polygones, les circonférences et autres coniques. D'où son importance dans la science et l'ingénierie, dont le développement a provoqué de manière significative.

D'un autre côté, la géométrie euclidienne a été la première science exacte, car avec elle le chemin de la systématisation de la science a commencé, ainsi que l'utilisation de la logique pour démontrer, à partir de quelques axiomes, de nombreuses propositions appelées théorèmes, afin de décrire les propriétés d'objets géométriques.

Histoire

La géométrie a une longue histoire, car l'intérêt de l'humanité à ce sujet est très ancien et l'axe central de la géométrie euclidienne est l'œuvre Articles, de l'Euclide sage d'Alexandrie, une ville située en Égypte, et qui a vécu au quatrième siècle pour.C.

À l'époque, les propriétés les plus importantes de nombreuses figures et corps géométriques étaient connus. Il y avait une connaissance approfondie de la géométrie, mais tout était empirique et manquait de systématisation.

Ensuite, le roi d'Égypte Ptolémée et a confié le professeur d'Euclide déjà célèbre, dont l'école était à Alexandrie, pour organiser toutes les connaissances mathématiques et géométriques disponibles jusqu'à présent, y compris les théorèmes et les propriétés.

Les euclides se sont mis au travail et à côté de ses disciples, ont écrit ses éléments de travail, qu'il a divisés en treize livres, en tant que chapitres. Ce travail deviendrait une référence pour la géométrie pour les générations futures.

Peut vous servir: dérivés successifs

Éléments d'Euclide

Le contenu des éléments est organisé comme suit:

• Dans les livres I à IV, la géométrie plate se développe.
• Dans les livres V et moi avons vu la théorie de la proportion.
• Les livres IX sont dédiés à l'arithmétique.
• L'ine-insesurabilité apparaît dans le livre x,
• La géométrie de l'espace dans les livres XI à XIII.

La géométrie euclidienne a été la base de nombreux développements géométriques postérieurs et est actuellement enseigné dans toutes les écoles du monde.

Il a également la vertu d'être le premier travail à inclure des démonstrations minutieuses basées sur un raisonnement logique, et aussi à donner une cohérence au corps de la connaissance géométrique et mathématique de cette époque.

Éléments de base de la géométrie euclidienne

La géométrie euclidienne est construite autour de quatre éléments de base, décrits dans le livre I des éléments:

1. Place
2. Droit
3. Plat
4. Espace

1. Place

UN place Il manque de dimensions ou de pièces et se distingue d'un autre point simplement par son emplacement. Si deux points A et B sont différents, c'est parce qu'ils ont des positions différentes, qui sont indiquées à travers les coordonnées cartésiennes bien connues (x, y) si le point est dans le plan ou les coordonnées (x, y, z) Si est dans l'espace.

Il est à noter que le système cartésien ne fait pas partie du Articles d'Euclid, mais est apparu beaucoup plus tard dans les 1600 années et est due à René Descartes.

2. Droit

La droit C'est une collection infinie de points, et il n'a que la longueur, pas la largeur. Une partie de celui-ci est généralement dessinée, avec des flèches en soulignant que la ligne continue indéfiniment.

3. Plat

UN plat C'est une surface illimitée, il a donc deux dimensions et dont une partie est représentée, au moyen d'un carré ou d'un rectangle.

Là, dans l'avion, il existe de nombreuses figures géométriques, telles que les lignes, les courbes ouvertes et fermées et les polygones, entre autres.

Peut vous servir: équation générale d'une ligne dont la pente est égale à 2/3

4. Espace

Enfin, il y a le espace Avec ses trois dimensions, capables de loger tous les points. Il contient les plans et les corps géométriques caractérisés par leur volume, comme les polyèdres, les sphères et plus.

Ceux-ci peuvent être considérés comme les définitions de base de la géométrie euclidienne, mais en plus de celles-ci, les eucléides offrent environ 150 définitions variées dans leur travail.

Notions courantes

Ils se composent de faits évidents et intuitifs, qui n'appartiennent pas correctement à la portée de la géométrie et sont utilisés comme concepts se développent. Ils se réfèrent aux «choses» dans un contexte très large:

1. Les choses à la même chose pour autre chose, elles sont les mêmes les unes avec les autres.
2. Si les choses sont ajoutées à un autre ensemble de choses, et toutes sont les mêmes, quels résultats sont aussi les mêmes.
3. Si des choses égales sont volées, le reste est également le même.
4. Lorsque les choses coïncident les unes avec les autres, c'est parce qu'ils sont les mêmes.
5. Le tout est toujours plus grand que les parties, prises séparément.

Postule de la géométrie euclidienne

Les postulats ou les axiomes sont des déclarations simples qui sont considérées comme vraies et évidentes, donc elles ne nécessitent pas de démonstration.

Ils constituent la base de la géométrie euclidienne et euclide établit cinq dans leur livre I:

1. Être deux points différents à et b, il n'y a qu'une seule ligne qui les traverse, c'est-à-dire que deux points déterminent une ligne.
2. Tout segment rectiligne peut être étendu indéfiniment pour constituer une ligne, par conséquent, chaque segment appartient à une ligne.
3. Si vous avez deux points différents ou A, vous pouvez toujours dessiner un cercle avec un centre en O et Radius égal au segment OA.
4. Tous les angles droits sont conformes les uns aux autres.
5. Étant donné une ligne et un point P qui ne lui appartient pas, c'est toujours possible.

Le dernier postulat, en particulier dans sa version originale, ne semble pas aussi simple que les autres. Il déclare que:

Peut vous servir: heptagone

«Si une ligne droite qui tombe sur deux autres lignes, rend les deux angles intérieurs du même côté inférieur à deux angles droits, ont déclaré des lignes droites, indéfiniment, ils sont (entrelacés) sur le côté sur lequel les angles mineurs sont que les angles sont que les angles sont que les angles sont que les angles sont que les anciens Deux angles droits ".

C'est-à-dire à l'origine le postulat 5 établit la condition pour que deux lignes ne soient pas parallèles. Mais il est plus clair lorsqu'il est écrit de telle manière qu'il illustre le contraire, c'est-à-dire le parallélisme des lignes.

Exemples de géométrie euclidienne

Exemple 1

Il y a trois points différents, étiquetés avec les lettres A, B et C.

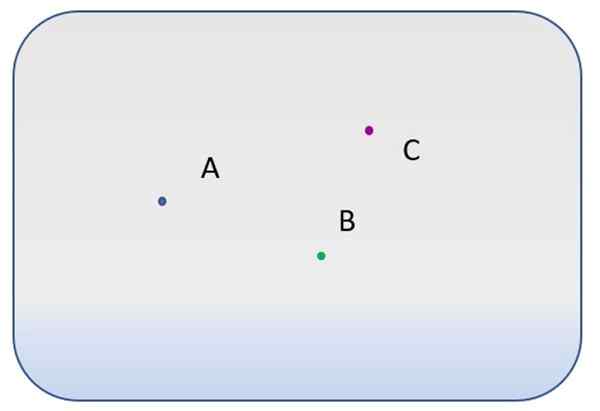
1. Combien de lignes différentes passent par point A?
2. Et combien peuvent être tracés entre les points A et B? Et entre A et C?
3. Est-il possible de tracer une ligne à laquelle pointe A, B et C?

Réponds à

Selon le postulat I, les lignes droites infinies peuvent être tracées à travers A, car deux points sont nécessaires pour déterminer une ligne.

Réponse b

Entre A et B ne peuvent être tracés qu'une ligne. Et entre A et C aussi.

Réponse C

Il n'est pas possible pour une ligne de contenir A, B et C en même temps.

Exemple 2

Il est demandé de construire étape par étape un triangle équilatéral (tous ses côtés sont égaux), connaissant l'un de ses côtés, qui est le segment AB et indiquant à chaque étape la postulat ou la notion commune utilisée dans la construction de la construction dans le.

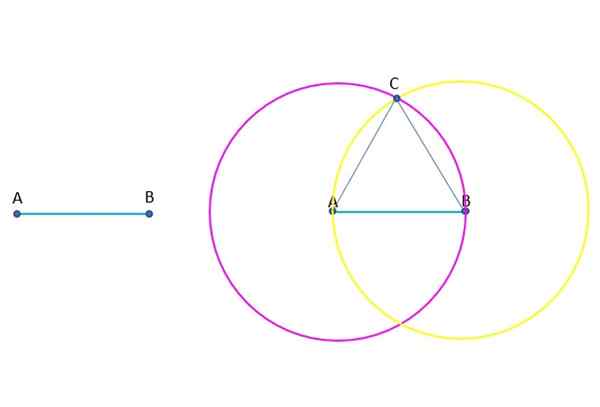Construction du triangle équilatéral ABC. Source: F. Zapata.

Répondre

Étape 1

Un cercle avec un centre dans A et Radio AB est dessiné. Cela est toujours possible, selon le postulat III.

Étape 2

Une autre circonférence avec Centre en B et Radio AB est dessinée, et le postulat III est à nouveau appliqué.

Étape 3

Les deux circonférences, qui ont le même rayon, sont coupées au point C. Maintenant, vous pouvez dessiner des segments qui unissent C avec A et B respectivement, selon le postulat I.

Ces segments sont des radios de la circonférence et donc les mesures de AC et BC sont égales à celles de l'AB, selon la notion commune 1. Alors le triangle ABC est équilatéral.