Matematiques

Fonctions vectorielles

555
30
Adrien Remy

Quelles sont les fonctions vectorielles?

Ongle fonction vectorielle d'un paramètre t, C'est une fonction dont le domaine sont les valeurs réelles de t, tandis que l'itinéraire est formé par des vecteurs de la forme r (t). Une telle fonction peut être exprimée comme suit:

r (t) = f (t) Toi + g (t) J + H (t) k

Où Toi, J et k Ce sont les vecteurs unitaires dans les trois principales directions de l'espace, et les fonctions F, G et H sont des fonctions réelles de la variable t. La notation utilise des grosses amplitudes vectorielles pour distinguer les amplitudes vectorielles.

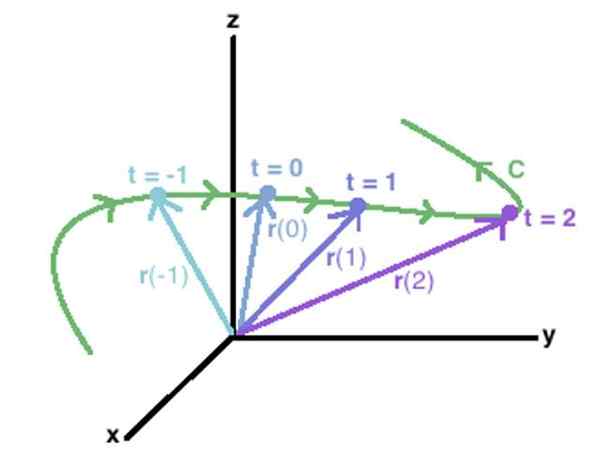Une fonction vectorielle dans l'espace peut être utilisée pour décrire une courbe C, joignant les points extrêmes de chacun des vecteurs déterminés par cette fonction. Source: Wikidot.

Une autre façon de désigner une fonction vectorielle est par les crochets:

r (t) = t), G (t), H (t)>

Les fonctions vectorielles peuvent être utilisées pour étudier les courbes dans le plan et l'espace, comme la trajectoire qui suit un objet en mouvement. Un exemple est la parabole décrite par une balle projetée avec une vitesse initiale, sous la gravité.

Si vous voulez connaître la position du ballon à chaque instant du temps t, La fonction vectorielle avec deux composants, un horizontal et une verticale:

r (t) = x (t) Toi + et(t) J

Les deux x (t) comme y (t) Ce sont des fonctions temporelles t. Ainsi, lorsque vous rejoignez les points extrêmes de chacun des vecteurs r(t) Possible, former la parabole décrite par la balle dans l'avion Xy.

Le concept s'étend facilement à une courbe C dans l'espace, comme celui illustré dans la figure ci-dessus. Les vecteurs y apparaissent r (-1), r (0), r (1) r (2), dont les extrémités tirent la courbe C, dessinée en vert.

Limites, dérivées et intégrales des fonctions vectorielles

Des outils de calcul qui s'appliquent à de véritables fonctions variables réelles peuvent également être appliquées aux fonctions vectorielles.

Peut vous servir: factorisation

Limite d'une fonction vectorielle

La limite de fonction vectorielle r (t) = f (t) Toi + g (t) J + H (t) k, Lorsque t → A, il est défini comme:

$\dpi110 \displaystyle \lim_t \to a\textbfr(t)=\left [ \displaystyle \lim_ t\to a f(t)\right ]\textbfi+\left [ \displaystyle \lim_ t\to a g(t)\right ]\textbfj+\left [ \displaystyle \lim_ t\to a h(t)\right ]\textbfk$

En supposant qu'il y a les limites respectives de f (t), G (t) et h (t), quand t → A.

Dérivé d'une fonction vectorielle

La définition de dérivé d'une fonction vectorielle r (t) = f (t) Toi + g (t) J + H (t) k Il est analogue à celui du dérivé d'une fonction réelle de la variable réelle. Appel r'(t) à ladite dérivée, vous avez:

$\dpi110 \mathbfr'(t)=\displaystyle \lim_\Delta t \to 0\frac\mathbfr(t+\Delta t)-\mathbfr(t)\Delta t$

Le dérivé existe chaque fois que la limite précédente existe, et si oui, la fonction r(t) est différenciable dans t.

Intégrale d'une fonction vectorielle

Être r (t) = f (t) Toi + g (t) J + H (t) k une fonction vectorielle, telle que les fonctions F, G et H sont intégrables dans t.

Ensuite:

$\dpi110 \int \mathbfr(t)dt =\left [ \int f(t)dt \right ]\mathbfi+\left [ \int g(t)dt \right ]\mathbfj+\left [ \int h(t)dt \right ]\mathbfk+\mathbfC$

Avec:

C = C₁Toi + c₂J

Ce qui signifie que la constante d'intégration est également un vecteur, mais constant.

Exemples de fonctions vectorielles

Exemple 1

Vous avez la fonction vectorielle donnée par r (t) = 3sec t Toi + 2tan t J. Il est possible de l'évaluer pour différentes valeurs t, telles que t = π / 4 et t = π, donnant naissance à des vecteurs r (π / 4) et r (π):

r (π / 4) = 3sec (π / 4) Toi + 2tan (π / 4) J = 3√2 Toi + 2 J

r (π) = 3sec (π) Toi+2TAN (π) J = - 3 Toi

Cependant, r (t) Il n'existe pas pour les valeurs de t = ∓π / 2, ∓3π / 2, ∓5π / 2…, puisque la fonction SEC t = 1 / cos t Il n'est pas défini, non plus t = sen t / cos t.

Par conséquent, le domaine de la fonction r (t) est toutes les valeurs réelles de t, sauf celles de la forme:

∓ (2n + 1) π / 2; Avec n = 0, 1, 2, .. .

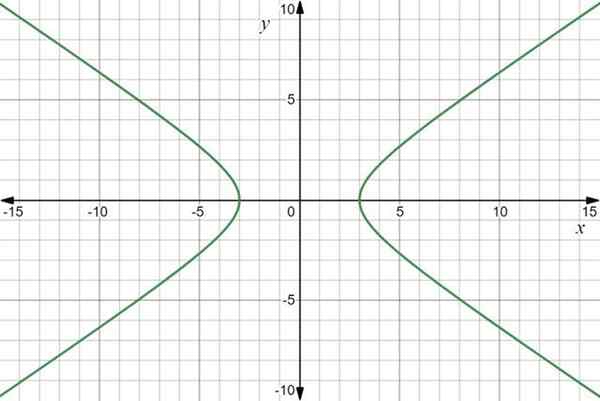
Le graphique de la fonction est une hyperbole:

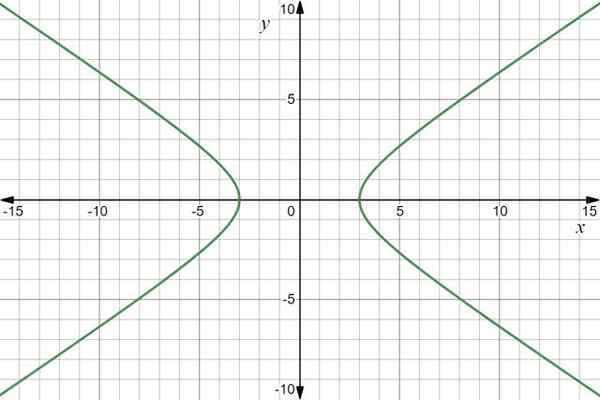Graphique de fonction vectorielle r (t) = 3sec t Toi+2 Tan T J. Source: F. Zapata à travers Desmos.

Exemple 2

Dans le lancement de projectile incliné, la position mobile est la fonction vectorielle r (t) = x (t) Toi + et(t) J . En supposant que la résistance à l'air n'intervient pas et que la gravité est la seule force qui agit sur le mobile, le mouvement horizontal est une rectiligne uniforme, tandis que la verticale est uniformément accélérée, étant g = 9.8 m / s² La valeur d'accélération. Cette accélération est verticale vers le sol.

Peut vous servir: règles de dérivation (avec des exemples)

Dans ce cas, les fonctions x (t) et (t) Ils sont respectivement:

x (t) = x_soit + V_bœuf∙ t
et (t) = y_soit + V_Oy∙ T - ½ GT²

Les montants v_bœuf et V_Oy Ce sont les composants de la fonction vectorielle qui décrit la vitesse mobile à tout moment:

V (t) = V_X(t) Toi + V_et(t) J

Avec:

V_bœuf = V_soit∙ cos θ
V_Oy = V_soit∙ Sen θ

Étant θ l'angle qui forme la vitesse initiale par rapport à l'horizontal.

Pour sa part, la position initiale du mobile est le point de coordonnée (x_soit,et_soit), ou de manière équivalente, le vecteur de position donné par:

r_soit (t) = x_soit Toi + et_soit J

Notez que, dans les équations indiquées, un signe négatif a été attribué à la direction verticale, de sorte que le troisième terme de l'équation pour y (t) le prend. Il est également possible d'attribuer l'origine à la position initiale du mobile.

Vitesse instantanée du projectile

La vitesse instantanée V (t) est la première dérivée de la position, en ce qui concerne le temps. Il est calculé en appliquant les règles de dérivation connues:

V(t) = R ' (t) = [x (t) Toi + et(t) J]]'= X '(t) Toi + et'(t) J = V_bœufToi + (V_Oy - Gt) J

Le module de vitesse est donné par:

$\dpi110 \left|\textbfv \right|=\sqrtv_ox^2+v_oy^2$

Accélération instantanée du projectile

On sait qu'il est g, dans la direction verticale et la direction vers le bas. Ceci est vérifié en sachant que l'accélération est la première dérivée de la vitesse par rapport au temps (ou le deuxième dérivé de la position par rapport au temps, s'il est préféré):

pour(t) = V ' (t) = [V_bœufToi + (V_Oy - Gt) J] '= [V_bœufToi] '+ [(V_Oy - Gt) J] '= = - g J

C'est précisément le résultat attendu.

Exercice résolu

Compte tenu de la fonction vectorielle r (t) = 3T Toi + (T - 1) J, trouver R '(t) et r "(T).

Solution

En appliquant les règles de dérivation à chacun des composants, vous avez:

Peut vous servir: constante d'intégration: signification, calcul et exemples

R '(t) = = 3 Toi + J

Et, puisque le dérivé d'une constante est 0:

r "(t) = 0

C'est-à-dire, r "(t) est égal au vecteur nul.

Les références

Figueroa, D. 2005. Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique. Édité par Douglas Figueroa (USB).
Larson, R. Calcul avec géométrie analytique. 2e. Édition. McGraw Hill.
Mathonline. Fonctions à valeur vectorielle. Récupéré de: Mathonline.Wikidot.com.
OpenTax. Volume de calcul 3. Récupéré de: OpenStax.org.
Purcell, E. J. 2007. Calcul. Pearson Education.