Fonctions trigonométriques de base, dans le plan cartésien, exemples, exercice

Le fonctions trigonométriques D'une variable réelle, ils correspondent à n'importe quel angle (exprimé en radianes), une raison trigonométrique, qui peut être sinus.

De cette façon, nous avons les six fonctions trigonométriques: sinus, cosinus, tangent, récolteuses, séchage et cotangente.

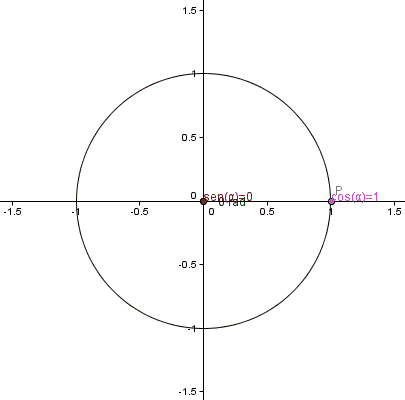Figure 1. Animation du cercle trigonométrique. Source: Wikimedia Commons.

Les fonctions trigonométriques pour les angles entre 0 et 2π sont définies à l'aide de la circonférence unitaire, de la radio 1 et dont le centre coïncide avec celui de l'origine du système de coordonnées cartésiennes: le point (0,0).

Nous pouvons localiser n'importe quel point P de coordonnées (x, y) sur cette circonférence.

Le segment qui unit l'origine avec P, ainsi que les segments respectifs qui unissent les projections de P sur les axes de coordonnées, constituent un triangle rectangle, dont les raisons trigonométriques sont appelées quotients entre les côtés du triangle. Donc:

• sin θ = opposé / Hypotenusa cateto
• cos θ = adjacent / Hypotenusa cateto
• Tg θ = Cateto opposé / Cateto adjacent

Et maintenant les raisons qui sont l'inverse de ce qui précède:

• sec θ = hypoténuse / cateto adjacent
• Dommage θ = hypotenusa / cateto en face
• CTG θ = Cateto adjacent / Cateto opposé

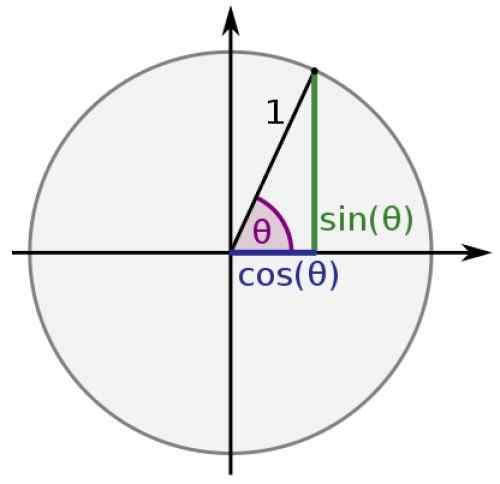
Dans le cercle unitaire, l'hypoténuse de tout triangle est égal à 1 et les catégories valent x et y, puis:

sin θ = y

cos θ = x

Figure 2. Le triangle droit dans le cercle unitaire. Source: Wikimedia Commons.

De cette façon, les fonctions sinus et cosinus acquièrent toujours des valeurs entre -1 et 1, tandis que les autres:

tg θ = y / x

dommage θ = 1 / y

Sec θ = 1 / x

Ils ne sont pas définis lorsque X soit et Ils valent 0.

[TOC]

Fonctions trigonométriques dans le plan cartésien

Comme nous le verrons ci-dessous, les fonctions trigonométriques sont caractérisées par le fait d'être périodique. Par conséquent, ils ne sont pas bijectifs, sauf dans un domaine restreint.

Fonction f (x) = sin x

À partir du cercle trigonométrique au point P (1.0), l'angle est 0 Radians. Ensuite, le rayon tourne dans un sens anti-horaire et la fonction Sen x se développe progressivement jusqu'à ce qu'elle atteigne π / 2 radians (90º), équivalent à 1.Environ 571 radians.

Peut vous servir: angles supplémentaires: quels sont les calculs, les exemples, les exercices

Là, il atteint la valeur y = 1 puis il diminue jusqu'à ce qu'il atteigne zéro dans π radianes (180 °). Par la suite, il diminue encore plus, car la valeur devient négative jusqu'à atteindre −1 lorsque l'angle est de 3π / 2 radians (270 °).

Enfin, il augmente à nouveau jusqu'à ce qu'il revienne à zéro à 360 °, où tout recommence. Cela fait y = sin x a fonction périodique de la période 2π, donc la fonction sinusale n'est pas bijective.

De plus, le graphique est symétrique par rapport au point (0,0), donc la fonction est impair.

Ensuite, le graphique de y = sen x:

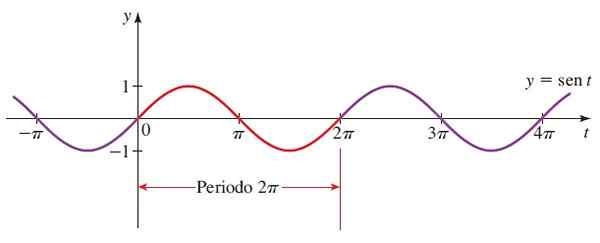figure 3. Fonction graphique f (x) = sin x. Source: Stewart, J. Préculaire: mathématiques pour l'université.

La section rouge est la première période. Les angles négatifs sont également pris en compte, car le rayon du cercle trigonométrique peut tourner dans un calendrier.

Domaine Sen x = Tous les réels.

Sen x gamme ou itinéraire = [-1,1]

Fonction f (x) = cos x

Au point P (1.0), la fonction coseno vaut 1 et à partir de là diminue, atteignant 0 lorsque l'angle est π / 2. Continuez à diminuer et prend des valeurs négatives, jusqu'à atteindre -1 à l'angle π.

Ensuite, il commence à augmenter progressivement jusqu'à ce qu'il atteigne 0 en 3π / 2 et reprend de la valeur lorsque le rayon a tourné un virage complet. De là, le cycle est répété, car Cos X est périodique et est également un couple (symétrique autour de l'axe vertical).

La forme de la fonction cosinus est la même que celle de la fonction sinusale, à moins qu'elles ne soient déplacées π / 2 par rapport à l'autre.

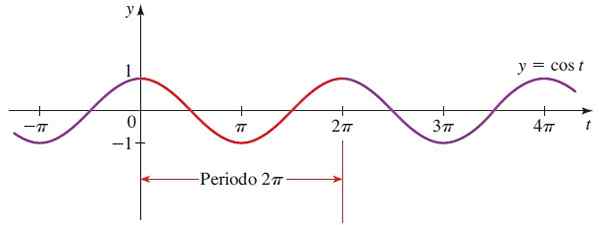Figure 4. Fonction graphique f (x) = sin x. Source: Stewart, J. Préculaire: mathématiques pour l'université.

Domaine cos x = Tous les réels.

Peut vous servir: estimation ponctuelle

Gamme ou route cos x = [-1,1]

Fonctions trigonométriques discontinues

Les fonctions TG X, CTG X, SEC X et HARS. Comme ceux-ci valent 0 sous certains angles, lorsqu'ils apparaissent dans le dénominateur, ils rendent la fonction discontinue.

Et puisque les sinus et le cosinus sont des fonctions périodiques, les fonctions TG X, CTG X, SEC X, dommage x sont également.

Fonction tangente f (x) = tg x

Pour la fonction tangente, les valeurs de discontinuité sont: ± π / 2, ± 3π / 2, ± 5π / 2 ... Là, la fonction prend des valeurs très grandes ou très petites. En général, cela se produit pour tous les multiples de π de la forme (2n + 1) π / 2, à la fois positif et négatif, avec n = 0, 1, 2 ..

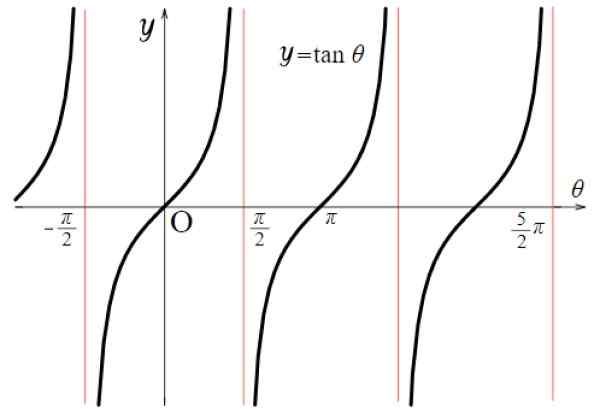Figure 5. Fonction graphique f (x) = tg x. Source: Wikimedia Commons.

Donc:

Domaine TG X: D = x ∈ R / x ≠ (2n + 1) π / 2; n ∈ Z

Tour de classement ou de TG X: Tous les réels.

Notez que la fonction f (x) = tg x est répétée entre - π / 2 et + π / 2, donc sa période est π. De plus, il est symétrique par rapport à l'origine.

Fonction cotangente f (x) = ctg x

Pour cette fonction, les valeurs de discontinuité se produisent en 0, ± π, ± 2π…, c'est-à-dire les multiples entiers de π.

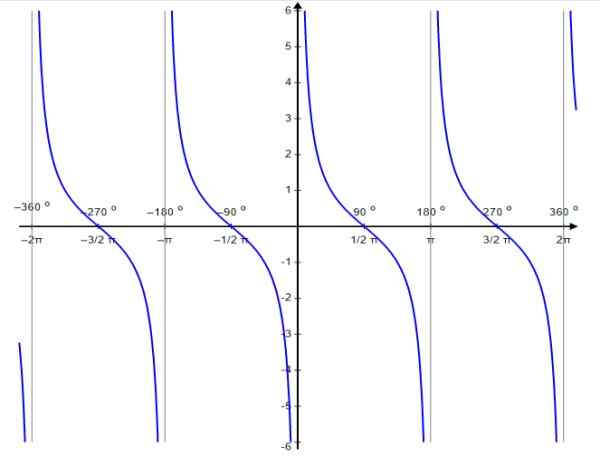Figure 6. Graphique de fonction f (x) = cotg x. Source: Wikimedia Commons.

Comme la fonction tangente, la fonction cotangente est une période périodique π. Pour elle, il est accompli que:

Domaine CTG X: D = x ∈ R / x ≠ n π; n ∈ Z

CTG x gamme ou itinéraire: Tous les réels.

Fonction de séchage f (x) = sec x

La fonction Sec x a des points de discontinuité dans ± π / 2, ± 3π / 2, ± 5π / 2…, où cos x = 0. Il s'agit également de période périodique π et est également observée du graphique que la fonction ne prend jamais de valeurs dans l'intervalle (-1,1)

Peut vous servir: nombres entiers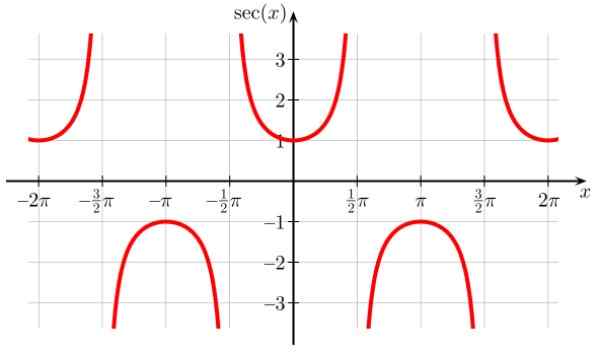 Figure 7. Fonction graphique f (x) = sec x. Source: Wikimedia Commons.

Doma de Sec x: D = x ∈ R / x ≠ (2n + 1) π / 2; n ∈ Z

Sec x Range ou route: Tous reais sauf (-1,1)

Fonction de récolte f (x) = dommage x

Il est similaire à la fonction de séchage, bien qu'il soit déplacé vers la droite, donc les points de discontinuité sont 0, ± π, ± 2π et tous les multiples entiers de π. C'est aussi périodique.

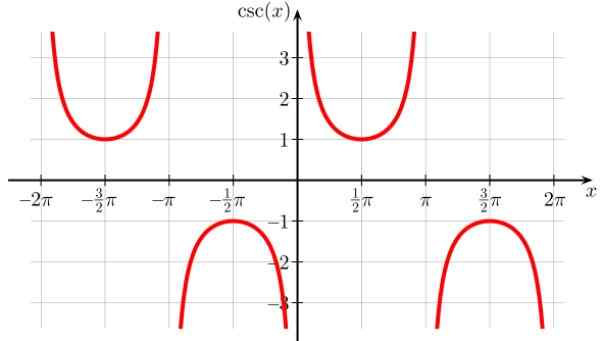Figure 8. Fonction graphique f (x) = dommage x. Source: Wikimedia Commons. Geek3 / cc by-sa (https: // CreativeCommons.Org / licences / by-sa / 4.0)

Domaine nuisible x: D = x ∈ R / x ≠ n π; n ∈ Z

Route de gamme ou d'harmonie: Tous reais sauf (-1,1)

Exercice résolu

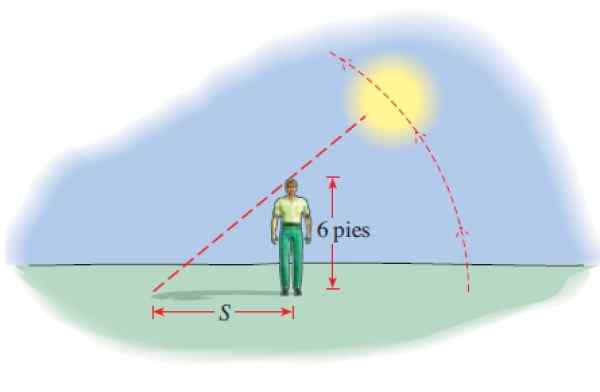
Un homme de 6 pieds de haut projette une teinte dont la longueur est donnée par:

S (t) = 6 │cot (π.T / 12) │

Avec s aux pieds et t le nombre d'heures après 6 heures du matin. Combien coûte l'ombre à 8 h, à 12 m, à 14 h et à 17 h 45?

Solution

Nous devons évaluer la fonction pour chacune des valeurs données, notez que la valeur absolue doit prendre, car la longueur de l'ombre est positive:

-À 8 heures du matin, 2 heures se sont écoulées à partir de 6 heures du matin, donc t = 2 et S (t) est:

S (2) = 6 │cot (π.2/12) │pies = 6 │cot (π / 6) │pies = 10.39 pieds.

-Quand il est 12 N, T = 6 heures se sont écoulées, donc:

S (6) = 6 │cot (π.6/12) │pies = 6 │cot (π / 2) │pies = 0 pieds. (À ce moment-là, le soleil tombe verticalement sur la tête de la personne).

-À 14 heures, ils ont passé t = 8 heures:

S (8) = 6 │cot (π.8/12) │pies = 6 │cot (2π / 3) │pies = 3.46 pieds.

-Quand il est 17h45, 11 ont passé 11.75 heures à partir de 6 heures du matin, alors:

S (11.75) = 6 │cot (π x 11.75/12) │pies = 91.54 pieds. Pour le moment, les ombres s'allongent.

Le lecteur peut-il calculer le moment où l'ombre de la personne est égale à sa hauteur?

Les références

1. Carena, m. 2019. Manuel des mathématiques de préunité. Université nationale de la côte.
2. Figuera, J. 1999. Mathématiques. 1er. Diversifié. Éditions collégiales bolivariennes.
3. Hoffman, J. Sélection de problèmes de mathématiques. Volume 4.
4. Jiménez, R. 2008. Algèbre. Prentice Hall.
5. Zill, D. 1984. Algèbre et trigonométrie. McGraw Hill.