Les fonctions de diplôme supérieures à deux (exemples)

A (polynôme) de grade supérieur à deux a la forme générale:

f (x) = a₀ + pour₁x + a₂X² +.. .pour_nXⁿ

Avec n = 3, 4, 5,…, un entier non négatif et les coefficients à_soit, pour₁… pour_n, qui sont généralement des nombres réels.

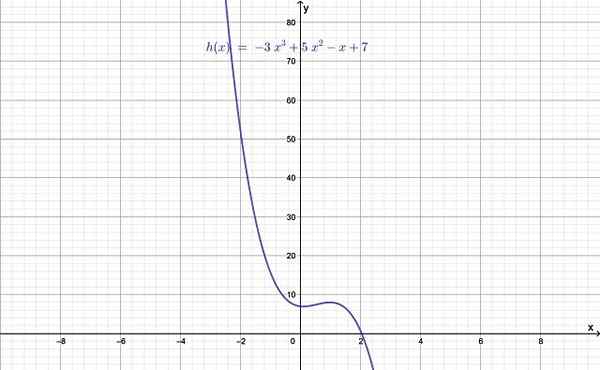Figure 1.- Graphique d'une fonction de diplôme supérieure à 2. Source: F. Zapata.

Le degré de la fonction est donné par la valeur de n, le plus grand des exposants et qui à son tour est supérieur à 2. Lorsque n = 0 est une fonction constante, si n = 1, c'est une fonction linéaire, et enfin avec n = 2, c'est une fonction quadratique.

Des exemples de fonctions de plus de deux, dans la variable "x", sont les suivants:

• f (x) = x³
• H (x) = - 3x³ + 5x² - X + 7
• g (x) = x⁴ - 6x² + 25

La fonction f (x) = x³ C'est le plus simple de toutes les fonctions de plus de deux et son degré est 3. Un degré 3 est également connu sous le nom fonction cubique. Pour sa part, G (x) est de la 4e année, pour être 4 l'exposant maximum.

La valeur de n est très importante car elle détermine la forme générale du graphique, ainsi que la quantité maximale de racines ou d'intersections que la fonction a avec l'axe horizontal. En effet, une fonction à 3 grade touchera l'axe horizontal au plus 3 points, l'un des gras 4 le fera au plus en 4 points et ainsi de suite.

Quant au terme indépendant, dans une fonction polynomiale de tout degré, il indique l'intersection de la fonction avec l'axe vertical.

Caractéristiques des fonctions polynomiales de plus de deux

Domaine

Le domaine d'une fonction est l'ensemble des valeurs qui permettent de calculer les valeurs de y = f (x). Pour les fonctions polynomiales, cet ensemble est celui des nombres N réels, ou l'ensemble de nombres complexes, si nécessaire pour étendre le domaine.

Peut vous servir: limites trigonométriques: comment les résoudre, résoudre des exercices

Signifie que, étant donné la fonction polynomiale f (x) = a₀ + pour₁x + a₂X² +.. .pour_nXⁿ, Vous pouvez toujours remplacer n'importe quel nombre réel, effectuer les opérations indiquées et obtenir en conséquence une valeur de réel y = f (x) réel.

Gamme

C'est l'ensemble formé par toutes les valeurs acquises f (x), c'est-à-dire les images que chaque valeur de X a via la fonction f (x). Pour les fonctions polynomiales supérieures à 2, cet ensemble est celui des nombres réels.

Racines de la fonction

Sont les valeurs de x pour lesquelles il est rempli que f (x) = 0. Comme indiqué ci-dessus, le degré de la fonction indique le nombre maximum de racines qu'elle peut avoir, bien que toutes ne soient pas nécessairement réelles.

Lorsque les coefficients de la fonction sont des nombres réels, les racines réelles correspondent aux intersections de la fonction avec l'axe x.

Exemple 1

Les racines rationnelles de la fonction f (x) = 2x³ - 9x² + 7x + 6 se trouve dans le théorème suivant:

Si la racine de f (x) = a₀ + pour₁x + a₂X² +.. .pour_nXⁿ C'est la forme b / c, donc les valeurs possibles de b sont des facteurs de a_soit et les valeurs possibles de c sont des facteurs de_n.

Pour la fonction de l'exemple, les combinaisons déjà simplifiées sont: ± 6, ± 3, ± 2, ± 1, ± 3/2, ± ½. Maintenant, chacun est testé via la procédure de division synthétique, par exemple. Lorsque le résidu de division est 0, la valeur éprouvée est une racine:

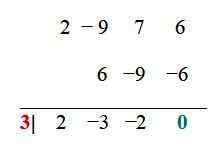
La valeur x₁ = 3 est une racine ou un zéro de la fonction, donc (x - 3) est un facteur commun de f (x), et cela peut être écrit comme:

Il peut vous servir: cercle unitaire: fonctions et applications trigonométriques

f (x) = (x - 3) ∙ (2x² −3x −2)

Les deux racines restantes sont les valeurs qui satisfont l'équation 2x² −3x −2 = 0. Cette équation peut être résolue à travers la formule générale, une calculatrice scientifique ou répéter le processus de tanteo précédent.

Ces racines sont x₂ = 2 et x₃ = - ½, et maintenant f (x) peut être écrit comme le produit de trois facteurs:

f (x) = (x - 3) ∙ (x - 2) ⋅ (x + ½)

Les intersections de f (x) avec l'axe x sont les points: P₁ (3.0), P₂(2.0) et p₃(−½, 0). Le graphique de la fonction, obtenu avec Geogebra, montre ses intersections avec l'axe x:

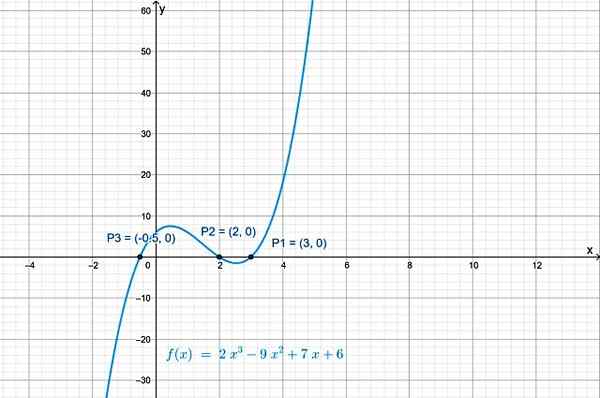Figure 2.- Une fonction polynomiale de grade 3 a trois intersections avec l'axe horizontal. Source: F. Zapata.

Intersection avec l'axe vertical

Pour trouver l'intersection de la fonction avec l'axe vertical, vous devez trouver f (0), qui est simplement de₀.

Exemple 2

Trouver l'intersection de f (x) = 2x³ - 9x² + 7x + 6 Avec l'axe vertical, il est très simple, lors de la fabrication de x = 0 dans f (x), il est obtenu:

f (x) = 6

Et le point d'intersection de la fonction avec l'axe vertical est p₄(0,6).

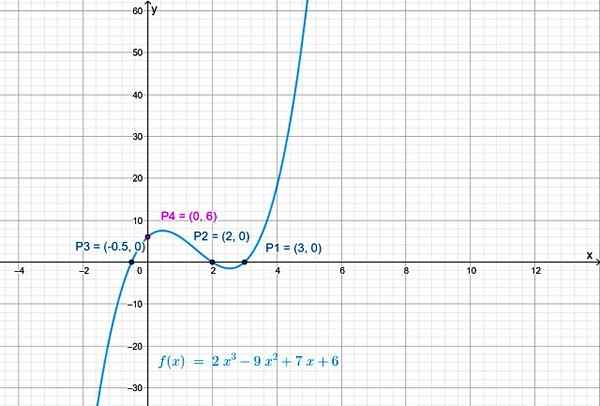figure 3. L'intersection de la courbe avec l'axe vertical fait x = 0 en f (x). Source: F. Zapata.

Continuité

Les fonctions polynomiques en général, et en particulier celles supérieures à 2, sont des fonctions continues dans leur domaine entier, cela signifie qu'ils n'ont pas de sauts, pas, trous ou valeurs pour lesquels ils ne sont pas définis. Ils n'ont pas non plus d'asymptotes, qui sont verticaux, horizontaux ou obliques directement à laquelle la fonction approche sans les traverser.

Ces qualités de douceur et de continuité sont appréciées dans les graphiques indiqués ci-dessus.

Graphique des fonctions supérieures à 2

Les graphiques des fonctions supérieurs à 2 sont continus et doux, et leur forme dépend du degré du polynôme.

Peut vous servir: permutations sans répétition: formules, démonstration, exercices, exemples

Par exemple, ceux de REAM de grade 3 Il a un signe négatif dans le terme avec le plus haut degré).

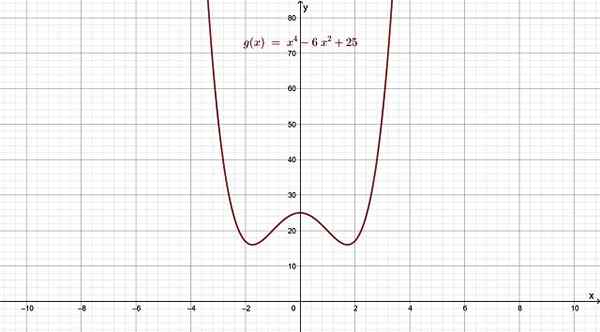Figure 4. Fonction polyinomique de la 4e année, dont le graphique ressemble à une lettre w. Source: F. Zapata.

Pour les valeurs de x loin de x = 0, à gauche et à droite, la fonction se comporte comment le plus grand degré ferait, car cela prévaut sur les autres lorsque x devient très grand ou très petit.

Dans l'image qui suit la fonction f (x) = 2x est comparé³ - 9x² + 7x + 6 avec la fonction r (x) = x³ Et il est apprécié que la forme des deux courbes est similaire aux valeurs de x qui sont bien loin de x = 0.

Pour les grandes valeurs x, la fonction croît rapidement en s'attendant à + ∞, tandis que pour les valeurs X négatives, la fonction diminue rapidement et tend à −∞.

Figure 5.- Toutes les fonctions de grade N se comportent de la même manière lorsqu'ils s'éloignent de x = 0, à gauche et à droite. Source: F. Zapata.

En comparant les courbes de grade de couple (figure 4) avec le degré impair (figure 2), tant que le coefficient qui accompagne le terme le plus élevé a le même signe, il est observé que les courbes de degré impair commencent à partir de «Y» négatif et négatif et se développent, tandis que ceux de la qualité cible commencent en "Y" positif et diminuer.

Les références

1. Barnett, R. 2000. Préculment: fonctions et graphiques. 4e. Édition. McGraw Hill.
2. Calcul.Dc. Fonctions polynomiques. Récupéré de: calcul.Dc.
3. Larson, R. 2012. Précalation. 8e. Édition. Cengage Learning.
4. Stewart, J. 2007. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
5. Varsity Tutorrs. Graphiquement des fonctions polynomiales. Récupéré de: WarsityTorm.com.