Une vraie fonction variable réelle et sa représentation graphique

Ongle Fonction variable réelle réelle Prenez un nombre appartenant à l'ensemble des nombres réels et l'associe à une autre valeur, également réelle, grâce à une règle de correspondance unique. Cela signifie que le nombre réel obtient, à travers cette règle, une image unique.

Les variables de départ numériques sont généralement désignées par la lettre X, tandis que leur image est la lettre et. D'un autre côté, à la règle de correspondance qui les relie est également appelée avec une autre lettre de l'alphabet, comme la fonction "F", bien qu'une autre puisse être utilisée.  En notation compacte, il est écrit:

f: x → y = f (x)

Figure 1. Graphique d'une vraie fonction polynomiale

À la variable  X on l'appelle variable indépendante, tandis que le et C'est le variable dépendante. La fonction peut être exprimée de plusieurs manières, par exemple à travers une déclaration mathématique comme celles-ci:

• f (x) = 2x −3
• H (x) = −3x²
• 

Une autre forme d'expression consiste à travers un graphique, ce qui est très utile car il vous permet d'apprécier le comportement de la fonction d'un seul regard. La construction d'un graphique est très simple à l'aide d'un système de coordonnées cartésiennes, dans lequel les pairs [x, f (x)] sont représentés comme des points dans l'avion. Ensuite, ils se joignent à une ligne douce et continue, vous pouvez voir comment la fonction est.

Exemples

Pour construire le graphique, vous pouvez recourir à un tableau des valeurs dans lesquelles les points à graphique sont placés. Pour les valeurs X variables, sont sélectionnées qui appartiennent au domaine de la fonction, c'est-à-dire celles qui, lorsqu'elles sont remplacées dans la formule, montrent à leur tour des nombres réels.

Une fois les valeurs de x choisies, son image y = f (x) est déterminée, et de cette manière les paires de points [x, f (x)] sont obtenues qui seront graphiques.

Peut vous servir: fonction homographique: comment graphiquement, exercices résolus

Il y a certains points qui sont importants et doivent être inclus dans le tableau: ceux dans lesquels le graphique coupe aux axes de coordonnées, que s'ils existent, car toutes les fonctions ne les coupent pas.

Pour les calculer, procédez comme suit:

-Intersection avec l'axe et: x = 0 est fabriqué dans la formule de fonction et la valeur correspondante est calculée.

-Intersection avec l'axe x: Y = 0 est terminé et l'équation f (x) = 0 est résolue.

Ensuite, le système de coordonnées cartésien est dessiné et chacun des points est tracé, qui sont ensuite joints à une ligne douce et continue si possible.

Exemple 1

Construisez un tableau des valeurs et le graphique de la fonction suivante:

f (x) = x² −4

Avant de commencer, vous devez trouver le domaine de la fonction, qui est l'ensemble des valeurs réelles pour lesquelles la fonction existe. Comme il s'agit d'une fonction quadratique, toute valeur X appartient aux nombres réels a une image réelle, selon F (x).

Ensuite, le tableau peut être construit en choisissant n'importe quelle valeur X, et la chose la plus simple est de commencer par les intersections du graphique avec les axes, s'il y a. Après les avoir trouvés, d'autres points sont recherchés pour terminer la table.

Pour x = 0

f (0) = -4

Par conséquent, le premier point du tableau est (0, -4). C'est l'intersection du graphique avec l'axe et.

Pour y = 0

Alors y = 0 est terminé et l'équation qui résultats est résolue:

X² −4 = 0

X² = 4

Les solutions de cette équation sont: x₁= 2 et x₂= -2. Par conséquent, il y a deux intersections avec l'axe x, qui sont les points: (−2,0) et (2.0).

Peut vous servir: nombres parfaits: comment les identifier et les exemples

Vous pouvez maintenant trouver plus de points à ajouter au tableau des valeurs:

Pour x = 1

f (1) = (1)² - 4 = −3

Pour x = - 1

f (−1) = (−1)² - 4 = −3

Pour x =  3

f (3) = (3)² - 4 = 5

Pour x =  -3

f (−3) = (−3)² - 4 = 5

Table de valeur

Le tableau suivant montre les points obtenus, qui serviront à construire le graphique de f (x):

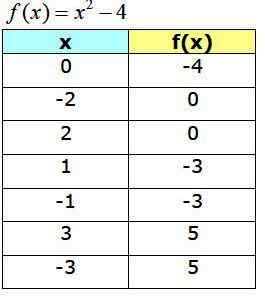Fonction graphique f (x) = x² −4

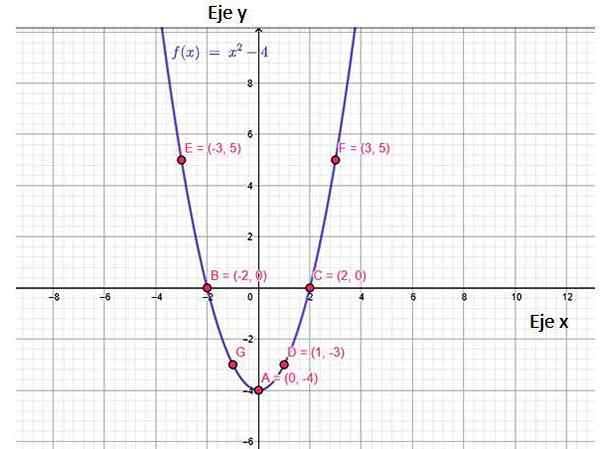Figure 2. Fonction F (x) Graphique de la fonction, montrant certains points qui lui appartiennent, y compris les intersections avec des axes. Source: F. Zapata, à travers Geogebra.

Le graphique de cette fonction est une parabole, qui s'ouvre et a à un point minimum, appelé sommet, de coordonnées (0, −4). Il est intéressant de noter que les valeurs de f (x) commencent à y = -4 à ∞. Ceci est la gamme de la fonction.

Du graphique, on peut conclure que la fonction est continue, diminuant dans l'intervalle (−∞, 0) et augmentant à partir de là.

Exemple 2

Ayant le tableau de la fonction, il est possible de connaître son domaine, sa gamme, les intersections qu'il a avec les axes et visualiser son comportement général (croissance et diminution).

Vous trouverez ci-dessous le graphique de la fonction polynomiale:

f (x) = - x⁴+4x²+1

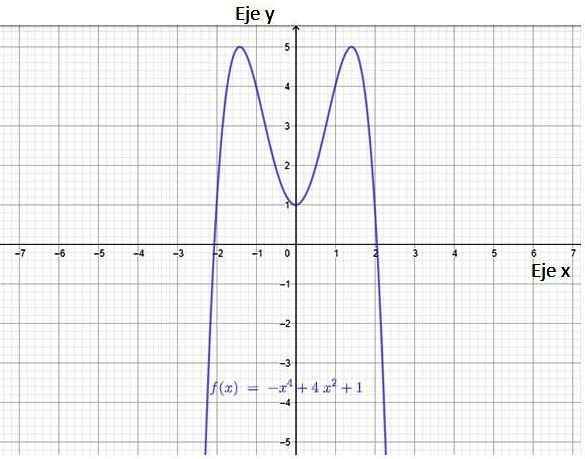figure 3. Graphique d'une fonction polynomiale. Source: F. Zapata à travers Geogebra.

De l'image, il s'ensuit que la fonction a deux intersections avec l'axe x, les points (-2,0) et (2.0). Il a également une intersection avec l'axe Y, le point (0,1).

Le domaine d'une fonction polynomiale est l'ensemble complet de nombres réels, il est également averti que la fonction est continue et a une symétrie autour de l'axe vertical. En effet, il peut être vérifié que cette fonction est Symétrie pour. Une fonction est même si elle se réunit:

Peut vous servir: théorème vert, démonstration, applications et exercices

f (x) = f (-x)

Le lecteur peut vérifier qu'en remplaçant -x dans la fonction, il n'est pas modifié.

Il y a deux points intéressants, qui sont à la hauteur de y = 5, sont les valeurs maximales de la fonction. La plage de cette fonction, c'est-à-dire l'ensemble de valeurs que la variable prend et, s'étend de -∞ à y = 5 précisément.

Pour connaître les valeurs de x dont l'image est y = 5, cette valeur est remplacée dans la fonction:

5 = - x⁴+4x²+1

Et cette équation est obtenue:

- X⁴ + 4x² - 4 = 0

Dont les solutions sont −√2 et + √2. Eh bien, la fonction est:

-Croissance De x -∞ à x = −√2

-Diminution De x = −√2 à x = 0

-Croissance De x = 0 à x = + √2

-Diminution À partir de x = + √2.

Exercice résolu

Construisez le graphique de la fonction suivante:

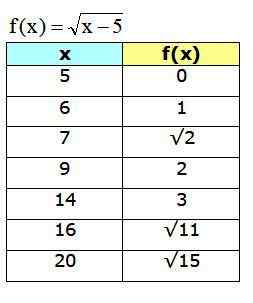
f (x) = √ (x-5)

Solution

Vous devez d'abord déterminer le domaine de la fonction, pour savoir quelles valeurs de x peuvent être choisies pour construire le tableau. Dans le cas de la fonction proposée, la quantité à l'intérieur de la racine doit toujours être positive ou égale à 0: par conséquent:

x - 5 ≥ 0

x ≥ 5

Par conséquent, seules des valeurs supérieures ou égales à 5 peuvent être choisies pour le tableau. Quant aux intersections avec les axes de coordonnées, la seule possibilité est de faire y = 0, puis x = 5.

Il est inutile de faire x = 0 pour cette fonction, car cette valeur n'appartient pas au domaine.

Le graphique obtenu est:

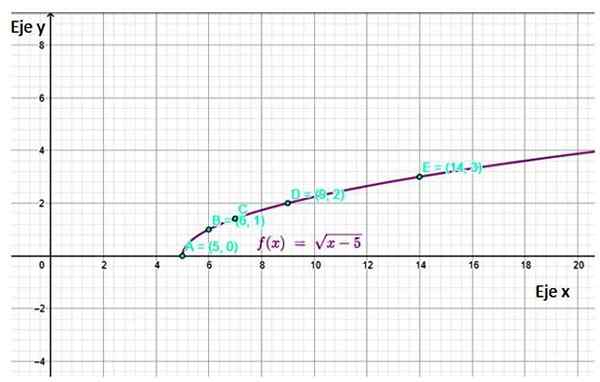Figure 4. Fonction graphique f (x) montrant certains des points calculés dans le tableau. Source: F. Zapata à travers Geogebra.

Les références

1. Zone électronique. Types de fonctions. Récupéré de: Emathzone.com.
2. Hoffman, J.g. Sélection de problèmes de mathématiques. Élégant. Spphinx.
3. Les mathématiques sont amusantes. Référence des fonctions communes. Récupéré de: Mathisfun.com.
4. Requena, b. Formules d'univers. Types de fonctions. Récupéré de: universoformules.com.
5. Stewart, J. 2006. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.