Fonction homographique comment graphiquement, exercices résolus

La fonctionÓn homographique ou rationnel Il s'agit d'un type de fonction mathématique composé de la division de deux composants polynomiaux. Il obéit à la forme p (x) / q (x), où q (x) ne peut pas prendre une forme nul.

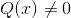
Par exemple, l'expression (2x - 1) / (x + 3) correspond à une fonction homographique avec p (x) = 2x - 1 y q (x) = x + 3.

Source: Pixabay.com

Les fonctions homographiques constituent une section d'étude des fonctions analytiques, traitée à partir de l'approche graphique et de l'étude du domaine et de la gamme. Cela est dû aux restrictions et fondations qui doivent être appliquées pour leurs résolutions.

[TOC]

Qu'est-ce qu'une fonction homographique?

Ce sont des expressions rationnelles d'une variable unique, bien que cela ne signifie pas qu'il n'y a pas d'expression similaire pour deux variables ou plus, où elle serait déjà en présence de corps dans l'espace qui obéissent aux mêmes modèles que la fonction homographique au niveau.

Ils ont de vraies racines dans certains cas, mais l'existence d'asymptotes verticales et horizontales est toujours maintenue, ainsi que la croissance et la diminution des intervalles. Généralement, une seule de ces tendances est présente, mais il existe des expressions capables de montrer les deux dans leur développement.

Son domaine est limité par les racines du dénominateur, car il n'y a pas de division entre zéro de nombres réels.

Fonction homographique mixte

Ils sont très fréquents dans le calcul, en particulier différentiel et complet, étant nécessaire pour dériver et anti-angel sous des formules particulières. Certains des plus courants sont classés ci-dessous.

Nième paire de fonctions homographiques

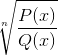
Exclut tous les éléments du domaine qui rendent l'argument négatif. Les racines présentes dans chaque polynôme montrent des valeurs zéro lorsqu'ils sont évalués.

Ces valeurs sont acceptées par le radical, bien que la restriction fondamentale de la fonction homographique soit considérée. Où q (x) ne peut pas recevoir de valeurs nulles.

Peut vous servir: fonctions transcendantes: types, définition, propriétés, exemples

Les solutions d'intervalle doivent être interceptées:

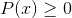
Pour atteindre les intersections, la méthode de signe peut être utilisée, entre autres.

Logarithme de la fonction homographique

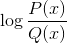
Exclut les valeurs de domaine qui lancent des intervalles négatifs et des zéros. Parce que les zéros sont déjà exclus du dénominateur, les solutions de: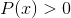

Il est également courant de trouver les deux expressions dans l'une, entre autres combinaisons possibles.

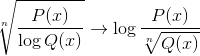
Comment représenter graphiquement une fonction homographique?

Les fonctions homographiques correspondent graphiquement avec des hyperbolas dans le plan. Qui sont transportés horizontalement et verticalement en fonction des valeurs qui définissent les polynômes.

Il y a plusieurs éléments que nous devons définir pour représenter une fonction rationnelle ou homographique.

Domaine

Le premier sera les racines ou les zéros des fonctions p et q.

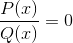
Les valeurs obtenues seront indiquées sur l'axe x des graphiques. Indiquant les intersections du graphique avec l'axe.

Asymptote vertical

Correspondent à des lignes verticales, qui délimitent le graphique en fonction des tendances qu'ils présentent. Ils touchent l'axe X dans les valeurs qui rendent le dénominateur zéro et ne seront jamais touchés par le graphique de la fonction homographique.

Asymptote horizontale

Représenté par une ligne de point horizontale, a délimité une limite pour laquelle la fonction ne sera pas définie au point exact. Les tendances seront observées avant et après cette ligne.

Pour le calculer, nous devons recourir à une méthode similaire à la méthode de l'Hopital, utilisée pour résoudre les limites des fonctions rationnelles qui ont tendance à l'infini. Les coefficients des pouvoirs les plus élevés du numérateur et le dénominateur de la fonction doivent être pris.

Par exemple, l'expression suivante a une asymptote horizontale à y = 2/1 = 2.

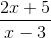
Intervalle de croissance

Les valeurs des commandés auront des tendances marquées dans le graphique en raison des asymptotes. En cas de croissance, la fonction passera des valeurs à mesure que les éléments du domaine de gauche à droite sont évalués.

Peut vous servir: 60 diviseurs

Diminution de l'intervalle

Les valeurs ordonnées diminueront à mesure que les éléments du domaine de gauche à droite sont évalués.

Les sauts trouvés dans les valeurs ne seront pas pris en compte à mesure que l'augmentation ou la diminution. Cela se produit lorsque le graphique est proche d'un vertical ou d'un horizont.

Intersection avec y

Faire de zéro la valeur de x, est l'intersection avec l'axe des ordonnées. C'est un fait très utile pour obtenir le graphique de la fonction rationnelle.

Exemples

Définissez le graphique des expressions suivantes, trouvez ses racines, ses asymptotes verticales et horizontales, la croissance et la diminution des intervalles et l'intersection avec l'axe de l'ordre.

Exercice 1

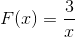
L'expression manque de racines, car elle a une valeur constante dans le numérateur. La restriction à postuler sera x différent de zéro. Avec asymptote horizontale à y = 0, et asymptote verticale à x = 0. Il n'y a pas de points d'intersection avec l'axe et.

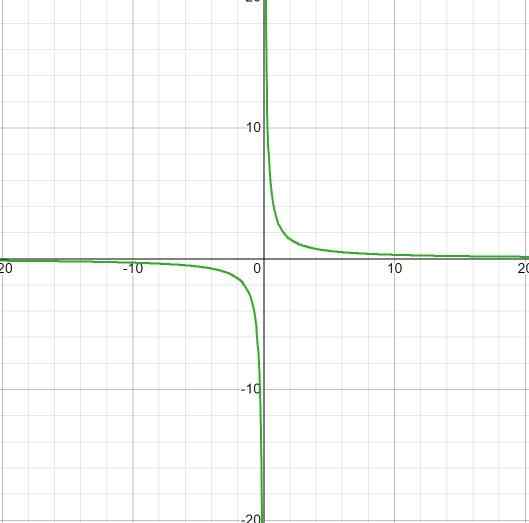
Il est observé qu'il n'y a pas d'intervalles de croissance même avec le saut de moins à plus infini dans x = 0.

L'intervalle de diminution est

Id: (-∞; o) u (0, ∞)

Exercice 1.2

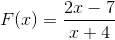
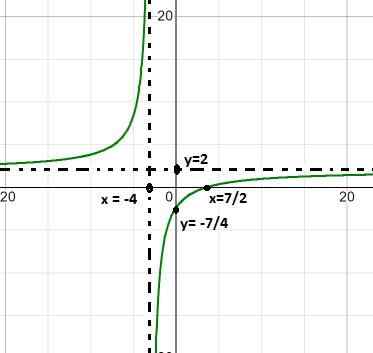
2 polynômes sont observés comme dans la définition initiale, nous procédons donc selon les étapes établies.

La racine trouvée est x = 7/2 qui résulte de l'égalisation de la fonction.

L'asymptote verticale est à x = - 4, qui est la valeur exclue du domaine en raison de la condition de fonction rationnelle.

L'asymptote horizontale est en y = 2, après avoir divisé 2/1, les coefficients des variables de grade 1.

Il a une intersection avec ceux qui ont été commandés à y = - 7/4. Valeur trouvée après égalisation le x à zéro.

Il peut vous servir: une fraction équivalente à 3/5 (solution et explication)

La fonction se développe constamment, avec un saut de plus à moins infini autour de la racine x = -4.

Son intervalle de croissance est (-∞, - 4) u (- 4, ∞).

Lorsque la valeur de x est proche de moins infinie, la fonction prend des valeurs proches de 2. La même chose se produit lorsque le X s'approche plus d'infini.

L'expression s'approche plus infinie lorsqu'elle est évaluée dans - 4 à gauche, et moins infinie lorsqu'elle est évaluée dans - 4 à droite.

Exercice 2

Le graphique de la fonction homographique suivante est observé:

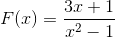
Décrivez leur comportement, leurs racines, leurs asymptotes verticaux et horizontaux, la croissance et la diminution des intervalles et l'intersection avec l'axe ordonné.

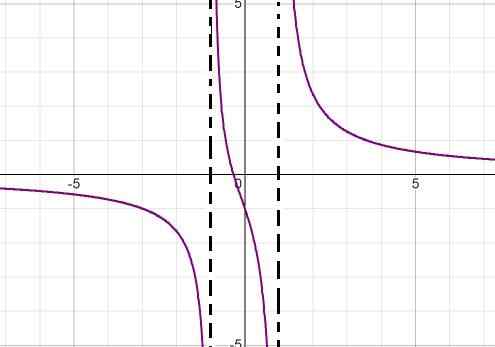
Le dénominateur d'expression indique en tenant compte de la différence de carrés (x + 1) (x - 1) les valeurs des racines. De cette façon, les deux asymptotes verticaux peuvent être définis comme:

x = -1 et x = 1

L'asymptote horizontale correspond à l'axe de l'abscisse car la puissance majeure est dans le dénominateur.

Sa seule racine est définie par x = -1/3.

L'expression diminue toujours de gauche à droite. Il s'approche de zéro lorsqu'il tend à l'infini. Moins infiniment à l'approche de -1 à gauche. Plus infini à l'approche de -1 à droite. Moins infini à l'approche de 1 à gauche et plus d'infini à l'approche 1 à droite.

Les références

1. Approximation avec des fonctions rationnelles. Donald J. Homme nouveau. Soc mathématique américain., 31 décembre. 1979
2. Fonctions de notation orthogonales. Université de La Laguna Tenerife Adhemar Bultheel, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen, Olav Njstad. Cambridge University Press, 13 février. 1999
3. Approximation de notation des fonctions réelles. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 mars. 2011
4. Fonctions algébriques. Gilbert Ames Bliss. Couer Corporation, 1 janvier. 2004
5. Magazine Spanish Mathematical Society, 5-6 volumes. Société mathématique espagnole, Madrid 1916