Fonction décroissante Comment l'identifier, exemples, exercices

Ongle fonction de diminution F est celui dont la valeur diminue à mesure que la valeur de X augmente. Signifie que dans un intervalle donné, considérant deux valeurs x₁ et x₂ tel que x₁ < x₂, puis f (x₁)> f (x₂).

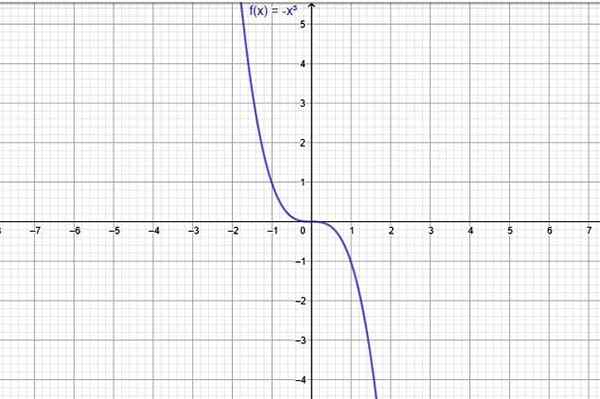
Un exemple de fonction qui diminue toujours est f (x) = -x³, dont le graphique montre dans la figure suivante:

Figure 1. Une fonction qui diminue toujours dans son domaine entier est f (x) = -x ^ 3. Source: F. Zapata à travers Geogebra.

Bien que certaines fonctions comme celle-ci soient caractérisées par la diminution de tout leur domaine, tous ne se comportent pas comme ça, il y a des augmentations et aussi celles qui se développent et diminuent dans certains intervalles de domaine. L'étude de la croissance et des intervalles de diminution est appelée monotonie de la fonction.

De même, la croissance ou la diminution de la fonction peut être prise en compte à un certain point de domaine. Mais toute fonction qui diminue dans un intervalle donné est également à chaque point qui lui appartient.

[TOC]

Comment identifier une fonction décroissante?

Le graphique de fonction indique visuellement s'il diminue ou non. Si, lorsque vous vous déplacez dans le sens croissant du X, la fonction "descend", cela signifie qu'il diminue.

Et si vous avez des intervalles dans lesquels il diminue et se développe alternativement, ce qui est le plus habituel, car ceux-ci sont clairement révélés en observant le comportement de la fonction dans tout son domaine, car il y aura des intervalles dans lesque qui "descendre".

Alternativement, si le graphique de fonction n'est pas disponible, analytiquement, il est possible de déterminer s'il diminue à un point ou dans un intervalle, à travers la première dérivée.

Critère du premier dérivé

Notez le comportement de la fonction décroissante illustrée à la figure 2. Les segments de ligne rose sont tangents aux points dont les coordonnées sont [A, F (A)] et [A + H, F (A + H)] et avoir une pente négative.

Peut vous servir: comment les informations sont-elles obtenues dans une enquête?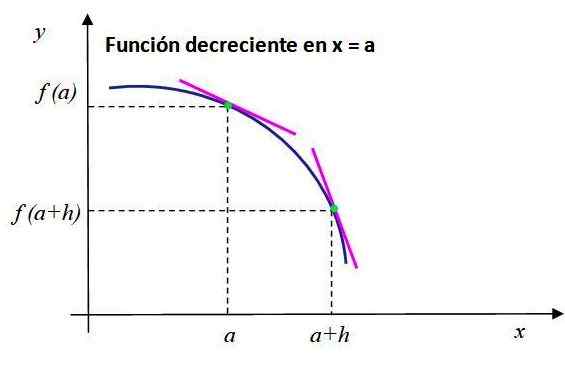Figure 2. La pente de la ligne tangente au graphique de f (x) est négative à x = a, alors la fonction diminue à ce stade. Source: F. Zapata.

Pour cette fonction, ce qui suit est rempli:

F (a + h) - f (a) < 0 ⇒  F (a + h) < f (a)

Par conséquent, on peut penser que la fonction diminue dans x = a.

Cependant, le premier dérivé de la fonction f (x), évalué à x = a, qui, par définition, est la pente de la ligne tangente à la courbe à x = a, est donnée par:

La limite indique que la valeur de H peut être fait aussi petite que vous le souhaitez et suggère que le signe de FA), Il peut être utilisé pour savoir si la fonction diminue ou non à un point particulier, tant que la dérivée existe à ce point.

Alors oui FA) < 0, On peut affirmer que la fonction diminue, et au contraire, si f '(a)> 0, Ensuite, la fonction augmente à ce moment.

Théorème pour la diminution et la croissance des fonctions

Auparavant, une référence a été faite au comportement de la fonction à un point. Maintenant, le théorème suivant permet de connaître les intervalles dans lesquels une fonction diminue, en croissance ou constante:

Soit F une fonction différenciable dans l'intervalle (a, b). C'est vrai que:

-Oui f '(x) < 0 para todo x perteneciente a (a,b), entonces f(x) es decreciente en (a,b).

-Si au contraire f '(x)> 0 pour tous les x appartenant à (a, b), il est dit que la fonction f (x) se développe (a, b).

-Enfin, si f '(x) = 0 pour tous les x qui appartiennent à l'intervalle (a, b), f (x) est constant dans ledit intervalle.

Manifestation

Supposons que f '(x) < 0 para cualquier valor de x en el intervalo (a,b), además se tienen x₁ et x₂ appartenant audit intervalle et à la condition que x₁< x₂.

Le théorème de valeur moyenne indique qu'il y a un nombre réel C, entre x₁ et x₂, tel que:

Peut vous servir: facteur commun pour le regroupement des termes: exemples, exercices

Comme établi depuis x₁< x₂,  Δx est positif. Donc, comme f '(c) est négatif, donc Δy est aussi. Donc f (x₁) est supérieur à f (x₂) Et la fonction diminue efficacement à tout point de l'intervalle (a, b).

Étapes pour savoir si une fonction diminue

Pour trouver les intervalles de diminution et de croissance d'une fonction en appliquant le théorème précédent, ces étapes sont suivies:

-Trouvez le premier dérivé de la fonction et faites-le correspondre à zéro, en résolvant l'équation résultante. Déterminer également les points auxquels le dérivé n'existe pas.

Tous ces points sont appelés points critiques Et il est nécessaire de les trouver, car en eux, le dérivé a la possibilité de changer leur signe, indiquant que la fonction passe de la croissance à la diminution ou au contraire.

-Le domaine de la fonction est divisé en intervalles déterminés par les points auxquels le premier dérivé est annulé ou n'existe pas.

-Enfin, le signe du dérivé est étudié à un point arbitraire qui appartient à chacun des intervalles obtenus à l'étape précédente.

Exemples de fonctions décroissantes

Les fonctions ne diminuent pas toutes au même rythme, certains le font plus rapidement que d'autres. Les fonctions suivantes, qui apparaissent fréquemment dans la pratique, diminuent:

La fonction exponentielle

Une fonction de la forme f (x) = a^X, Avec un entre 0 et 1, sans l'inclure, diminue rapidement dans tout leur domaine.

Fonction 1 / x

Grâce à un programme graphique en ligne en tant que Geogebra, le graphique de la fonction f (x) = 1 / x est construit, confirmant qu'il diminue dans son domaine entier.

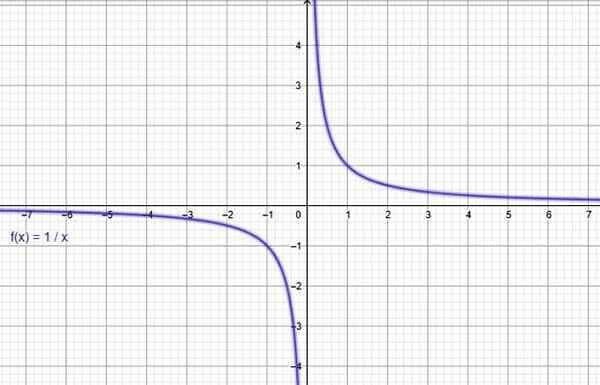figure 3. La fonction f (x) = 1 / x diminue. Source: F. Zapata à travers Geogebra.

La fonction connexe

Les fonctions de la forme y = mx + b avec m<0 tienen gráficas que son rectas de pendiente negativa y por lo tanto son funciones decrecientes.

Peut vous servir: égalité mathématique

Exercice résolu

Trouvez, le cas échéant, les intervalles de diminution de la fonction:

f (x) = x⁴ - 6x² - 4

Solution

La première étape consiste à trouver f '(x):

f '(x) = 4x³ - 12X

La première dérivée de f (x) est une fonction continue, c'est-à-dire qu'elle n'a pas de points de discontinuité, mais est annulé dans:

4x³ - 12x = 0 = 4x (x²-3) = 0

Les solutions de cette équation sont: x₁ = 0, x₂ = - √3 et x₃ = √3. Ce sont les points critiques qui divisent le domaine de f (x) dans les intervalles: (-∞, - √3); (- √3.0); (0, √3); (√3, ∞ +).

Alors le premier dérivé d'une valeur x arbitraire est évalué, qui appartient à chaque intervalle. Ces valeurs ont été choisies:

Pour (-∞, - √3)

F '(-2) = 4 (-2)³ - 12x (-2) = -32 + 24 = -8

Pour (- √3.0)

F '(-1) = 4 (-1)³ - 12x (-1) = -4 + 12 = 8

Pour (0, √3)

f '(1) = 4 (1)³ - 12x (1) = 4-12 = -8

Pour (√3, ∞ +)

f '(2) = 4 (2)³ - 12x (2) = 32-24 = 8

Comme plusieurs intervalles, c'est une bonne idée de faire une table pour organiser les résultats. La flèche vers le haut indique que la fonction augmente et baisse, ce qui diminue:

Il est conclu que la fonction diminue aux intervalles (-∞, - √3) et (0, √3) et croît dans les intervalles restants. La fonction originale de Geogebra est facilement vérifiée en graphiquement.

Les références

1. Ayres, f. 2000. Calcul. 5ed. Mc Graw Hill.
2. Leithold, L. 1992. Calcul avec géométrie analytique. Harla, s.POUR.
3. Purcell, E. J., Varberg, D., & Rigdon, s. ET. (2007). Calcul. Mexique: Pearson Education.
4. Matemobile. Fonctions, en croissance, en diminution et constante. Récupéré de: Matemovil.com
5. Stewart, J. 2006. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.