Fonction bijective Qu'est-ce que, comment se fait-il, des exemples, des exercices
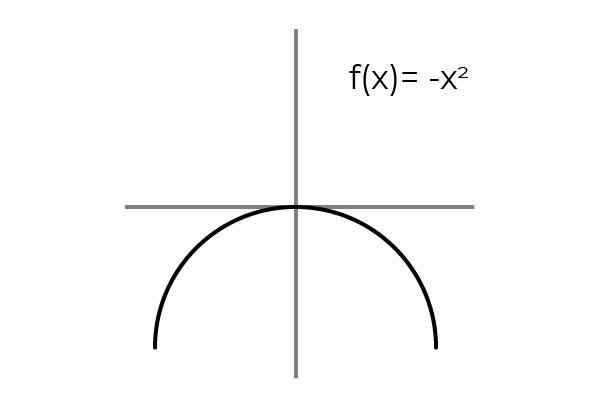
- 3083
- 735
- Noa Da silva
Ongle Fonction bijective C'est celui qui répond à la double condition d'être Injectif et surjectif. C'est-à-dire que tous les éléments du domaine ont une seule image dans la codominium, et à son tour, le codominium est égal à la plage de la fonction ( RF ).
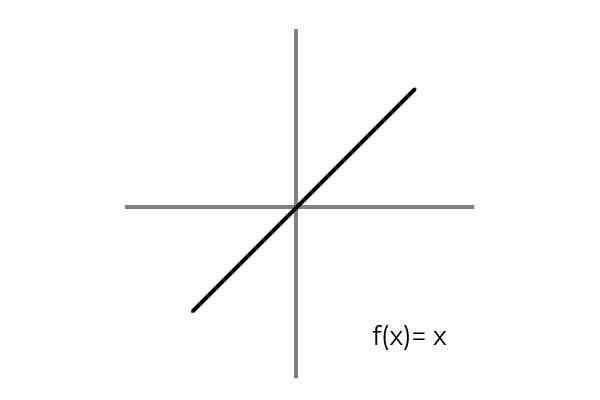
Il est satisfait lorsqu'une relation biunivoque entre les éléments du domaine et de la codominium est considérée. Un exemple simple est la fonction F: R → R défini par la ligne F (x) = x
 Source: auteur
Source: auteur Il est observé que pour chaque valeur du domaine ou de l'ensemble de départ (les deux termes s'appliquent également), il y a une seule image dans le codominium ou l'ensemble d'arrivée. De plus, il n'y a aucun élément de codominium qui n'est pas l'image.
De cette façon F: R → R défini par la ligne F (x) = x est bijectif
[TOC]
Comment est une fonction de bijjectif?
Pour répondre à cela, il est nécessaire d'avoir des concepts clairs liés à Injectivité et Sur la surjectivité d'une fonction, En plus des critères de conditionnement des fonctions pour les adapter aux exigences.
Injectivité d'une fonction
Une fonction est Injectif Lorsque chacun des éléments de son domaine est lié à un seul élément de codominium. Un élément de codominium ne peut être qu'une image d'un seul élément du domaine, de cette manière les valeurs de la variable dépendante ne peuvent pas être répétées.
À envisager Injectif Les éléments suivants doivent être remplis à une fonction:
∀ x1 ≠ x2 ⇒ f (x1 ) ≠ f (x2 )
Sur la surjectivité d'une fonction
Une fonction est classée comme Surcourir, Si chaque élément de son codominium est une image d'au moins un élément de domaine.
À envisager Surcourir Les éléments suivants doivent être remplis à une fonction:
Peut vous servir: échantillonnage de remplacementÊtre F: DF → CF
∀ b ℮ CF ET à ℮ DF / F (a) = b
C'est la façon algébrique d'établir que pour chaque «b» qui appartient à CF Il y a un "A" qui appartient à dF de sorte que la fonction évaluée dans "A" est égale à "B".
Conditionnement des fonctions
Parfois une fonction qui n'est pas Bijectif, peut subir un certain conditionnement. Ces nouvelles conditions peuvent le transformer en un Fonction bijective. Tous les types de modifications du domaine et de la codominium de la fonction sont valides, où l'objectif est de répondre aux propriétés d'injectivité et de surex.
Exemples: exercices résolus
Exercice 1
Être la fonction F: R → R défini par la ligne F (x) = 5x +1
A: [Tous les nombres réels]
Il est observé que pour toute valeur de domaine, il y a une image dans la codominium. Cette image est unique, ce qui fait F être une Fonction d'injectif. De la même manière, nous observons que le codominium de la fonction est égal à sa gamme. Réalisant ainsi la condition de Sur-objectivité.
Être injectif et sur-objectif en même temps que nous pouvons conclure que
F: R → R défini par la ligne F (x) = 5x +1 c'est une Fonction bijective.
Cela s'applique à toutes les fonctions linéaires (fonctions dont le plus grand degré de variable est un).
Exercice 2
Être la fonction F: R → R Défini par F (x) = 3x2 - 2
Lors du dessin d'une ligne horizontale, il est observé que le graphique se trouve à plusieurs reprises. À cause de cela la fonction F Ce n'est pas injectif et donc ce ne sera pas Bijectif Tout en étant défini dans R → R
De la même manière, il existe des valeurs de codominium qui ne sont pas des images d'un élément de domaine. Pour cette raison, la fonction n'est pas sur place, ce qui mérite également de conditionner l'ensemble d'arrivée.
Peut vous servir: Théorie des ensembles: caractéristiques, éléments, exemples, exercicesLe domaine et la codominium de la fonction sont conditionnés
F: [0 , ∞] → [- 2 , ∞ ]]
Où il est observé que le nouveau domaine couvre les valeurs de zéro à l'infini positif. Éviter la répétition des valeurs qui affectent l'injectivité.
Ainsi, le codominium a été modifié, comptant de «-2» à l'infini positif, éliminant de la codominium les valeurs qui ne correspondaient à aucun élément de domaine
De cette façon, il peut être assuré que F : [0 , ∞] → [- 2 , ∞ ]] Défini par F (x) = 3x2 - 2
C'est bijectif
Exercice 3
Être la fonction F: R → R Défini par F (x) = sin (x)
Dans l'intervalle [ -∞ , +∞ ]] La fonction des sinus varie ses résultats entre zéro et un.
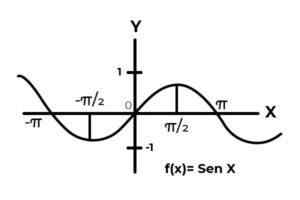 Source: auteur.
Source: auteur. La fonction F Il ne correspond pas aux critères d'injectivité et de surjection, car les valeurs variables dépendantes sont répétées chaque intervalle π. De plus, les termes de la codominium en dehors de l'intervalle [ -onze ] Ils ne sont pas l'image d'aucun élément de domaine.
Lorsque vous étudiez les graphiques de fonction F (x) = sin (x) des intervalles sont observés où le comportement de la courbe répond aux critères de Bijectivité. Comme l'intervalle DF = [ π / 2,3π / 2 ]] Pour le domaine. ET CF = [-1, 1] Pour codominium.
Où la fonction varie des résultats de 1 à -1, sans répéter aucune valeur dans la variable dépendante. Et en même temps le Co -oominium est égal aux valeurs adoptées par l'expression Péché (x)
De cette façon la fonction F: [ π / 2,3π / 2 ] → [-1, 1] Défini par F (x) = sin (x). C'est bijectif
Exercice 4
Augmenter les conditions nécessaires pour dF et CF. Pour que l'expression
Peut vous servir: Erreur d'échantillonnage: formules et équations, calcul, exemplesF (x) = -x2 Être bijection.
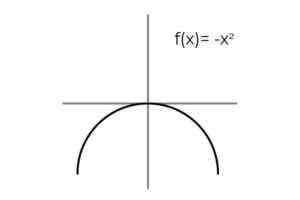 Source: auteur
Source: auteur La répétition des résultats est observée lorsque la variable prend des valeurs opposées:
F (2) = f (-2) = -4
F (3) = f (-3) = -9
F (4) = f (-4) = -16
Le domaine est conditionné, le limitant au côté droit de la ligne réelle.
DF = [0 , +∞ ]]
De la même manière, il est observé que la plage de cette fonction est l'intervalle [ -∞ , 0], qui, en servant de codominium, remplit les conditions de la surjectivité.
De cette façon, nous pouvons conclure que
L'expression F: [0 , +∞ ] → [ -∞ , 0] Défini par F (x) = -x2 C'est bijectif
Exercices proposés
Vérifiez si les fonctions suivantes sont bijectives:
F: [0 , ∞) → R Défini par F (x) = 3 (x + 1)2 +2
F: [ 3π / 2,5π / 2 ] → R Défini par F (x) = 5ctg (x)
F: [ -π,π ] → R Défini par F (x) = cos (x - 3)
F: R → R défini par la ligne F (x) = -5x + 4
Les références
- Introduction à la logique et à la pensée critique. Merrilee H. Saumon. Université de Pittsburgh
- Problèmes d'analyse mathématique. Piotr Bilar, Alfred Witkowski. Université de Wroclaw. Pôle.
- Éléments de l'analyse abstraite. Mícheál o'searcoïd doctorat. Département des mathématiques. University College Dublin, Beldfield, Dublind 4
- Introduction à la logique et à la méthodologie des sciences déductives. Alfred Tarski, New York Oxford. Oxford University Press.
- Principes d'analyse mathématique. Enrique Linés Escardó. Reverté éditorial. Jusqu'en 1991. Barcelone Espagne.
- « Structure du glycogène, synthèse, dégradation, fonctions
- Caractéristiques des enzymes caractéristiques, mécanismes d'action, exemples »

