Force élastique ce qui consiste, formules et exercices

La force élastique C'est la force qu'un objet exerce pour résister à un changement dans sa forme. Il se manifeste dans un objet qui a tendance à récupérer sa forme lorsqu'il est sous l'action d'une force de déformation.

La force élastique est également appelée force réparatrice car elle s'oppose à la déformation pour retourner des objets à sa position d'équilibre. Le transfert de la force élastique se fait par les particules qui intègrent les objets.

Force élastique d'un printemps

Par exemple, lorsqu'un ressort métallique est comprimé, une force qui pousse les particules de ressort est exercée en réduisant la séparation entre elles, en même temps, les particules résistent à être poussées exerçant une force contraire à la compression.

Si au lieu de comprimer le ressort, il est lancé, s'étirant, les particules qui l'intégrent sont plus séparées. De même, les particules résistent à séparer une force contraire à l'étirement.

Les objets qui ont la propriété de récupérer leur forme d'origine par la force de déformation opposée sont appelés objets élastiques. Les ressorts, le caoutchouc élastique et les cordes élastiques sont des exemples d'objets élastiques.

[TOC]

Quelle est la force élastique?

La force élastique (F_k) C'est la force qu'un objet exerce pour récupérer son état d'équilibre naturel en ayant été affecté par une force extérieure.

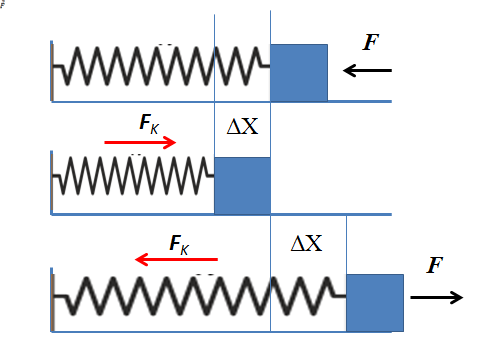
Pour analyser la force élastique, le système de masse de printemps idéal sera pris en compte qui se compose d'un ressort horizontalement placé sous réserve d'une extrémité sur le mur et à l'autre bout d'un bloc de masse méprisable. Les autres forces agissant sur le système telles que la friction ou la force de gravité ne seront pas prises en compte.

Il peut vous servir: deuxième condition d'équilibre: explication, exemples, exercices

Si une force horizontale est exercée sur la pâte, dirigée vers le mur, il est transféré au ressort le comprimant. Le ressort se déplace de sa position d'équilibre vers une nouvelle position. Comme l'objet a tendance à rester en équilibre, la force élastique se manifeste au printemps qui s'oppose à la force appliquée.

Le déplacement indique à quel point le ressort et la force élastique ont été déformés est proportionnel à ce déplacement. Lorsque le ressort est comprimé, la variation de la position augmente et augmente par conséquent la force élastique.

Plus le ressort est comprimé, plus la force d'opposition exerce jusqu'à ce qu'elle atteigne un point où la force appliquée et la force élastique sont équilibrées, par conséquent le système de masse de ressort cesse de bouger. En arrêtant d'appliquer la force, la seule force agissant est la force élastique. Cette force accélère le ressort dans la direction contraire à la déformation jusqu'à la récupération de l'état d'équilibre.

De la même manière, il se produit lors de l'étirement du ressort en regardant la pâte horizontalement. Le ressort est étiré et exerce immédiatement une force proportionnelle au déplacement opposé à l'étirement.

Formules

La formule de force élastique est exprimée par la loi de Hooke. Cette loi établit que la force élastique linéaire exercée par un objet est proportionnelle au déplacement.

F_k = -K.Δs         [1]

F_k = Force élastique

k = Constante de proportionnalité

Δs = Déplacement

Lorsque l'objet se déplace horizontalement, comme dans le cas du ressort soumis au mur, le déplacement est ΔX, Et l'expression de la loi de Hooke est écrite:

F_k = -K.ΔX        [2]

Peut vous servir: lentille convergente: caractéristiques, types et exercices résolus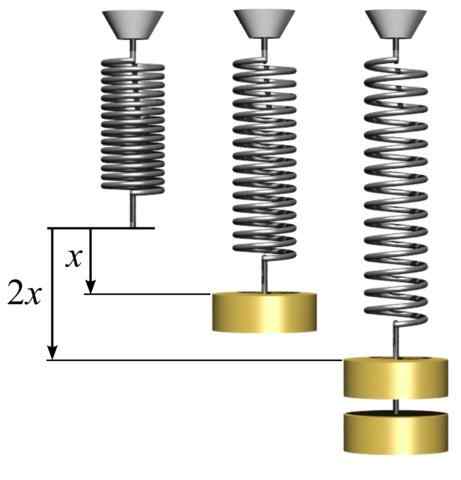la loi de Hooke. Force élastique proportionnelle à l'étirement. [Par svjo (https: // communes.Wikimedia.org / wiki / fichier: hookes-law-springs.Png)]

Le signe négatif de l'équation indique que la force élastique du ressort est dans la direction opposée à la force qui a provoqué le déplacement. La proportionnalité constante k C'est une constante qui dépend du type de matériel auquel le ressort est constitué. L'unité de la constante k est N / m.

Les objets élastiques ont une limite d'élasticité qui dépendra de la constante de déformation. S'il s'étend au-delà de la limite élastique, elle se déformera de façon permanente.

L'équation [1] et [2] s'applique aux petits déplacements de ressort. Lorsque les déplacements sont plus importants, des termes sont ajoutés avec une plus grande puissance de ΔX.

L'énergie cinétique et l'énergie potentielle ont fait référence à une force élastique

La force élastique fonctionne sur le ressort en le déplaçant vers sa position d'équilibre. Pendant ce processus, l'énergie potentielle du système de masse de printemps augmente. L'énergie potentielle due au travail effectué par la force élastique est exprimée dans l'équation [3].

U = ½ K .  Δx²[3]

L'énergie potentielle est exprimée en Joules (J).

En arrêtant d'appliquer la force de déformation, le ressort accélère à la position d'équilibre en diminuant l'énergie potentielle et en augmentant l'énergie cinétique.

L'énergie cinétique du système de masse à ressort, lorsque la position d'équilibre atteint, est déterminée par l'équation [4].

ET_k= ½ m.V²[4]

m = masse

V = vitesse de ressort

Pour résoudre le système de masse de printemps, la deuxième loi de Newton est appliquée en tenant compte que la force élastique est une force variable.

Exercices pratiques d'exemples

Obtention de la force de déformation

Combien de force est nécessaire pour appliquer à un ressort pour étirer 5 cm si la constante de ressort est de 35 n / m?

Peut vous servir: Accélération de la gravité: qu'est-ce que c'est, comment il est mesuré et exerce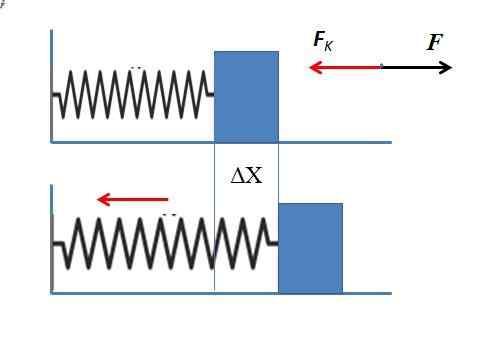Force élastique d'un ressort qui s'étend 5 cm

Comme la force de l'application est opposée à la force élastique est déterminée F_k en supposant que le ressort est étiré horizontalement. Le résultat ne nécessite pas le signe négatif car la force d'application est uniquement nécessaire.

la loi de Hooke

F_k = -K.Δx       

La constante k du printemps est 35n / m.

Δx = 5cm = 0,05 m

F_k = -35n / m . 0,05 m

F_k = - 1,75n = - f

On a besoin 1,75 N de force pour déformer le printemps 5 cm.

Obtention de la constante de déformation

Quelle est la constante de déformation d'un ressort qui s'étend 20 cm par l'action d'une force de 60N?

Δx =20 cm = 0,2 m

F = 60N

F_k = -60n = - f

K = - f_k / Δx

  = - (-60N) /0.2M

K = 300 n / m

La constante de ressort est 300N / m

Obtenir une énergie potentielle

Quelle est l'énergie potentielle référée au travail effectué par la force élastique d'un ressort qui est comprimé 10 cm Et sa constante de déformation est 20N / m?

ΔX =10 cm = 0,1 m

K = 20 n / m

F_k = -20N / M . 0,1 m

F_k = -200N

La force élastique du printemps est -200n.

Cette force fonctionne sur le ressort pour le déplacer vers sa position d'équilibre. Lors de l'exécution de ce travail, l'énergie potentielle du système augmente.

L'énergie potentielle est calculée avec l'équation [3]

U = ½ K .  Δx²

U = ½ (20N / m) . (0,1 m)²

U = 0,1 boule

Les références

1. Kittel, C, Knight, W D et Ruderman, M A. Mécanique. États-Unis: Mc Graw Hill, 1973, Vol. Toi.
2. Rama Reddy, K, Badami, S B et Balasubramanian, V. Oscillamements et vagues. Inde: University Press, 1994.
3. Murphy, J. Physique: sous-juge les propriétés de la matière et de l'énergie. New York: Britannica Educational Publishing, 2015.
4. Giordano, n j. Physique du collège: raisonnement et relations. Canada: Brooks / Cole, 2009.
5. Walker, J, Halliday, D et Resnick, R. Fondamentaux de la physique. États-Unis: Wiley, 2014.