Matematiques

Fractions équivalentes à 3/4

1474
440
Lucas Schneider

Le fractions équivalentes à 3/4 Ce sont ceux dans lesquels, en divisant le numérateur entre le dénominateur, il en résulte le numéro décimal 0.75.

C'est toujours possible. Si le résultat de cette opération est égal à 0.75, la fraction équivaut à 3/4, par exemple, fraction 6/8:

La fraction 6/8 est équivalente à ¾, car, en divisant le numérateur entre le dénominateur, dans les deux cas 0 est obtenu.75. Source: F. Zapata.

Maintenant, la fraction 6/8 a été obtenue en multipliant à la fois le numérateur et le dénominateur ¾. En multipliant simultanément le numérateur et le dénominateur de la même quantité, la valeur décimale d'une fraction donnée n'est pas modifiée, mais permet d'obtenir des fractions qui équivalent à une donnée.

Une autre façon de trouver une fraction équivalente à un autre serait de diviser le numérateur et le dénominateur du même montant. Cependant, dans le cas de ¾, il n'est pas possible de trouver un tel nombre qui se divise en même temps à 3 et 4 et le résultat est entier. En effet.

Lorsque le numérateur et le dénominateur d'une fraction sont des nombres premiers les uns avec les autres, on dit que la fraction est irréductible. Par conséquent, ¾ est irréductible.

Façons de trouver une fraction équivalente à un autre

Il existe deux façons très simples de trouver une fraction équivalente à une autre fraction donnée: la première est par réduction et la seconde par amplification.

Réduction et amplification des fractions

Réduction

Cette procédure consiste à trouver un nombre diviseur à la fois du numérateur et du dénominateur. Une fois trouvés, le numérateur et le dénominateur sont divisés par cette valeur et ont immédiatement obtenu une fraction équivalente à l'original. Il est vérifié qu'il fait ainsi le rapport numérique entre le dénominateur et la comparaison.

Peut vous servir: fonctions mathématiques

Quand la fraction irréductible d'un autre. La fraction ainsi obtenue est irréductible.

La fraction ¾ est irréductible, comme indiqué précédemment, pour être 3 et 4 cousins les uns avec les autres, mais la méthode suivante permet des fractions infinies équivalentes à ¾.

Amplification

Pour amplifier une fraction donnée, le numérateur et le dénominateur doivent être multipliés par la même quantité, peu importe s'il s'agit d'un nombre positif ou négatif. Par exemple, la fraction 6/8 a été obtenue en amplifiant ¾ par le facteur 2:

$\frac34=\frac3\times 24\times 2=\frac68$

Bien que les fractions aient un numérateur et un dénominateur différent, les deux sont les mêmes.

Notez la figure suivante, qui contient deux cercles identiques, divisés en parties égales, bien que de taille différente. Observant soigneusement, les zones en vert et en violet ont la même mesure, mais la zone verte a été subdivisée en 3 parties, du 4 au total qui composent le cercle de la gauche. D'un autre côté, le cercle à droite était subdivisé en 8 parties égales et la zone violette est équivalente à 6 d'entre elles.

De cette façon, vous pouvez graphiquement que ¾ équivaut à 6/8, car les deux fractions représentent le même montant.

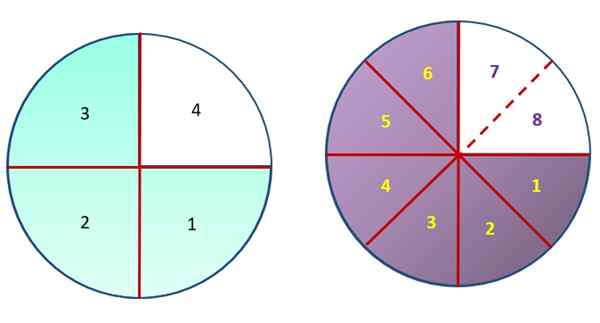Les fractions ¾ et 6/8 représentent la même zone dans les deux cercles. Source: F. Zapata.

En général, si la fraction est multipliée ¾ par le nombre de n, de nombreuses fractions qui s'y équivalent sont obtenues comme vous le souhaitez:

$\frac34=\frac3\times n4\times n=\frac3n4n$

Il est important de noter que n ne peut jamais être égal à 0, car la division de 0 n'est pas définie. Aucune fraction ne peut avoir 0 dans votre dénominateur.

Comment savoir si une fraction équivaut à 3/4?

Comme expliqué au début, un moyen de savoir si une fraction équivaut à ¾ est de faire le quotient entre le numérateur et le dénominateur. Si c'est 0.75, la fraction est équivalente à ¾, mais il existe quelques méthodes supplémentaires à savoir, qui ne nécessitent pas directement de division:

Il peut vous servir: médias pondérés: comment il est calculé, exemples et exercices

Méthode 1

Supposons que la fraction A / B, et vous voulez savoir si cela équivaut à ¾, c'est-à-dire s'il est vrai que:

$\frac34=\fracab$

Pour être équivalent, le produit 4 doit être égal au produit 3B:

4a = 3b

Méthode 2

Si la fraction A / B est équivalente à ¾, en divisant A et B par son diviseur MCD commun maximum, le résultat doit être ¾.

Pour clarifier l'utilisation de ces méthodes, consultez les exemples suivants.

Exemples

Exemple 1

Déterminez si la fraction 150/200 est équivalente à ¾:

Par méthode 1

Dans ce cas A = 150 et B = 200, il faut le réaliser:

4a = 3b

4 × 150 = 600
3 × 200 = 600

Il est conclu que 150/200 est équivalent à ¾.

Par méthode 2

Le diviseur commun maximum de 150 et 300 les divise tous les deux exactement. Les deux quantités se décomposent dans leurs facteurs premiers, puis les facteurs communs avec leur moindre exposant sont multipliés:

150 = 2 × 5² × 3
200 = 2³ × 5²

Les 2 et 5 sont communs, ils multiplient en choisissant le moindre puissance avec lequel ils apparaissent:

MCD (150, 200) = 2 × 5² = 2 × 25 = 50

Maintenant, nous procédons à la division:

$\frac150200=\frac150 \div50 200\div 50=\frac34$

Exercices résolus

Exercice 1

Écrivez par amplification cinq fractions équivalentes à ¾, multipliant le numérateur et le dénominateur à chaque fois par les nombres entiers suivants:

a) 3, b) 5, c) (-2), d) 10 et e) 20

Solution à

$\frac3 \times 3 4\times 3=\frac912$

Solution B

$\frac3 \times 5 4\times 5=\frac1520$

Solution C

$\frac3 \times (-2) 4\times (-2)=\frac-6-8=\frac68$ Notez qu'il n'y a pas de différence en amplifiant la fraction de 2 ou -2, car selon la règle des signes, le quotient indiqué entre deux quantités négatives est positive.

Solution d

$\frac3 \times 10 4\times 10=\frac3040$

Solution E

$\frac3 \times 20 4\times 20=\frac6080$ Notez que cette fraction est la même que celle obtenue en amplifiant par 2 la fraction obtenue ci-dessus:

$\frac30 \times 2 40\times 2=\frac6080$