Fractions équivalentes à 2/3

Le fractions équivalentes à ⅔ (Les deux tiers sont lus) sont ceux dont la valeur, exprimée de manière décimale, est la même celle qui est obtenue en divisant 2 par 3: 0.6666… les points suspendus indiquent que 6 apparaît des temps infinis dans cette division.

Une fraction équivalente à 2/3 est la fraction 4/6, car il s'avère qu'après avoir résolu la division entre 4 et 6 explicitement, la décimale 0,6666 .. . Ensuite, on peut dire que 4/6 = 2/3 = 0,6666 .. .

Les fractions 2/3 et 4/6 sont équivalentes car en divisant le nombre du numérateur par le chiffre du dénominateur, le même numéro de journal 0,66666 .. . (Source: F. Zapata)

Une fraction, comme son nom l'indique, est une partie ou une partie de l'unité. La fraction ⅔ est obtenue en divisant l'unité en trois parties égales et en prenant deux de ces parties.

Chaque fraction se compose d'une partie supérieure, appelée numérateur, séparé du fond ou dénominateur, À travers la ligne de fraction. Le dénominateur indique le nombre de pièces que l'unité est divisée et le numérateur indique combien de ces parties doivent être prises en considération.

Considérez maintenant la fraction 4/6 (lire quatre sixième). Il est prouvé que cette fraction équivaut à ⅔, car pour diviser l'unité en six parties, ces étapes doivent être suivies:

1. Divisez l'unité en trois parties égales.
2. Puis diviser chacune de ces parties de moitié, obtenant au total six parties égales.

Si 4 parties de 1/6 de l'unité sont regroupées, la quantité obtenue est une fraction de valeur identique à laquelle 2 parties de 1/3 de l'unité sont obtenues. Dans le graphique suivant, la procédure décrite est effectuée: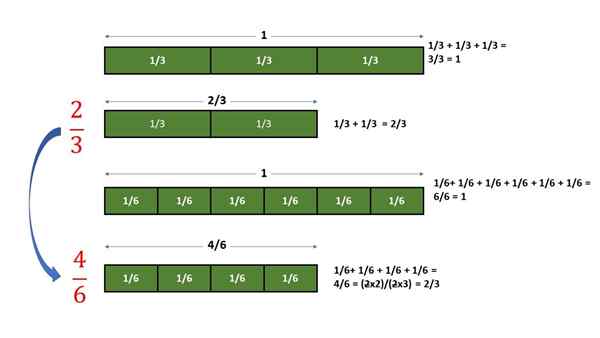

Vérification graphique que la fraction 2/3 est équivalente à la fraction 4/6. Source: F. Zapata.

Peut vous servir: analogies numériques: types, applications et exercices

Méthodes pour trouver des fractions équivalentes

Notez que la fraction équivalente 4/6 peut être obtenue à partir de 2/3 en multipliant à la fois par le numérateur et le dénominateur de ce dernier.

Lorsque vous multipliez simultanément le numérateur et le dénominateur d'une fraction par le même nombre, une fraction équivalente est obtenue.

Une autre façon de trouver une fraction équivalente à un autre serait de diviser le numérateur et le dénominateur du même montant, à condition que le numérateur et le dénominateur soient exactement divisibles par ce même numéro. Mais il n'est pas possible d'atteindre, par division par le même entier, une fraction équivalente basée sur 2/3, puisque les nombres 2 et 3 sont des cousins ​​les uns avec les autres.

Lorsque le numérateur et le dénominateur d'une fraction sont des nombres premiers les uns avec les autres, on dit que la fraction est irréductible. Et la fraction 2/3 est un bon exemple de ce type de fractions, en fait, 2/3 représente l'ensemble de toutes les fractions équivalentes à 0.666 ..

D'un autre côté, la fraction 4/6 est réductible et équivalente à la fraction ⅔, car le numérateur 4 et le dénominateur 6 sont même des nombres, tous deux divisibles par 2.

Ainsi, les deux façons d'obtenir des fractions équivalentes à une don, sont:

• Amplifier simultanément le numérateur et le dénominateur 
• Réduire le numérateur et le dénominateur

Amplification des fractions

Pour obtenir une fraction équivalente à une donnée, le numérateur et le dénominateur sont multipliés par la même figure. Voici quelques exemples:

Il est conclu que ⅔ (deux tiers), 4/6 (quatre sixième), 6/9 (six neuvième) et 8/12 (huit douze) sont tous des fractions équivalentes les uns avec les autres, mais d'eux, seuls ⅔ est l'agréctible fraction.

En résumé, si vous partez de la fraction irréductible ⅔, le moyen d'obtenir une autre fraction équivalente est d'appliquer cette formule:

Peut vous servir: exercices de factorisation résolus

Avec un entier.

Méthode d'amplification pour obtenir des fractions équivalentes. Source: F. Zapata

Réduction des fractions

Il s'agit d'une méthode qui permet d'obtenir une fraction équivalente, à condition que la fraction de départ ait un numérateur et un dénominateur avec un ou plusieurs diviseurs communs.

Ce n'est pas le cas de 2/3, qui comme dit précédemment, est irréductible. Mais par exemple, la fraction 60/90 (soixante années 90) Il peut être réduit à:

• 6/9, puisque le numérateur et le dénominateur sont divisibles entre dix.
• 30/45, car le numérateur et le dénominateur sont divisibles entre deux.
• 20/30, puisque le numérateur et le dénominateur sont divisibles entre trois.
• 12/18, car le numérateur et le dénominateur sont divisibles entre cinq.

Si vous souhaitez obtenir la fraction irréductible équivalente à l'original, il est nécessaire de diviser à la fois le numérateur et le dénominateur par son diviseur commun maximum (MCD).

Décomposer dans les facteurs du numérateur:

60 = 2² ⋅ 3 ⋅ 5

Et effectuer la même procédure dans le dénominateur:

90 = 2 ⋅ 3² ⋅ 5

Les MCM sont les facteurs premiers communs avec son exposant inférieur, c'est-à-dire:

MCM (60; 90) = 2⋅3⋅5 = 30

Puis, 60 entre 30 da 2, qui est placé dans le numérateur et à 90 entre 30 da 3, 3 est placé dans le dénominateur. Par conséquent, la fraction irréductible 60/90 peut être exprimée comme suit:

Façons de déterminer si une fraction donnée équivaut à 2/3

La façon directe de savoir si deux ou plusieurs fractions sont équivalentes, est d'exprimer les fractions directement de manière décimale, et si tous les chiffres coïncident, il est certain que les fractions sont équivalentes. Mais il existe d'autres méthodes applicables à 2/3:

Méthode 1

Être fraction x / y vous voulez savoir si cette fraction équivaut à 2/3:

Un panneau d'interrogatoire est placé, car on ne sait pas encore si les valeurs de "x" et "y" satisfont l'égalité. Pour le savoir, il se multiplie en croix:

Peut vous servir: Relations de proportionnalité: concept, exemples et exercices

3x =? 2 et

Ce n'est que lorsque l'égalité est remplie, il y a certitude que X / Y est une fraction équivalente à 2/3.

Méthode 2

Cette méthode nécessite de déterminer le diviseur commun maximum (MCD) du numérateur et du dénominateur. Alors les deux sont divisés par le MCD, et si la fraction obtenue après effectuer l'opération décrite est 2/3, alors on peut dire qu'il s'agit d'une fraction qui équivaut à elle.

Exemples

Exemple 1

Déterminer si la fraction 40/60 est équivalente à ⅔.

Solution

Par méthode 1:

La méthode indique qu'elle doit être multipliée en croix:

40 x 3 =? 60 x 2

120 =? 120

Étant donné que l'égalité est remplie, il est conclu que 40/60 équivaut à 2/3.

Exemple 2

Déterminez si la fraction 120/180 est équivalente à ⅔.

Solution

Dans cet exemple, la méthode 2 s'applique. La première chose est de déterminer la décomposition des facteurs premiers de 120:

120 = 2³ ⋅ 3 ⋅ 5

Et la décomposition des facteurs de dénominateur est:

180 = 2² ⋅ 3² ⋅ 5

Pour déterminer le MCD, les facteurs communs sont multipliés par son exposant inférieur:

MCD (120; 180) = 2² ⋅ 3 ⋅ 5 = 60

Ensuite:

120 ÷ 60 = 2

180 ÷ 60 = 3

Il est donc conclu que 120/180 équivaut à 2/3, c'est-à-dire:

Exercices résolus

Exercice 1

Sont des fractions 10/15 et 12/18 équivalent?

Solution

Le moyen le plus rapide de le vérifier est de se multiplier en croix, car ce ne sont pas de très grandes valeurs:

10 x 18 =? 15 x 12

180 =? 180

Une égalité a été obtenue, puis on peut dire que 10/15 = 12/18.

Exercice 2

Sont des fractions 8/12 et 12/20 équivalentes à ⅔?

Solution

La méthode de simplification sera appliquée, qui consiste à diviser simultanément un numérateur et un dénominateur par des facteurs premiers communs jusqu'à atteindre une expression irréductible:

12/12 = 4/6 = ⅔, c'est-à-dire que la première fraction est équivalente à ⅔.

Pour la deuxième fraction que vous avez:

12/20 = 6/10 = ⅗, mais ⅗ est irréductible et différent de ⅔, donc la deuxième fraction ne équivaut pas à ⅔.