Flux de champ électrique

Qu'est-ce que le flux de champ électrique?

Il flux de champ électrique ou simplement l'écoulement électrique est une quantité scalaire proportionnelle au nombre de lignes de champ électrique qui traversent une surface. Il est indiqué par la capitale capitale φ (PHI).

Le champ électrique ne "s'écoule" pas comme le fait un flux d'eau, bien que les lignes d'écoulement du fluide ressemblent à celles du champ électrique.

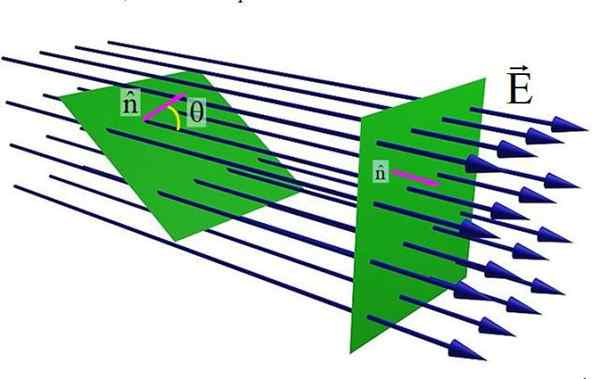
Figure 1. Le champ électrique s'écoule à travers une surface plate. Source: Wikimedia Commons.

La figure supérieure montre une surface plate traversée par un champ électrique ET. Lorsque l'unité normale vectorielle à la surface n Et le champ ET Ils sont parallèles, la quantité de lignes de champ qui traverse la surface est maximale. Mais à mesure que l'angle θ augmente entre n et ET, Le nombre de lignes passées à travers la surface verte est inférieure.

D'un autre côté, le flux de champ électrique dépend également de l'ampleur de ET, Parce que plus cela est élevé, plus ils traversent la surface des lignes de champ. Et bien sûr, plus la zone s de ladite surface est grande, également l'écoulement, donc l'équation suivante est établie:

Φ = e ∙ sosθ

Cette expression est cohérente avec le produit scalaire parmi les vecteurs ET et n:

Φ = (ET • n) S

L'unité de flux de champ électrique dans le système international d'unités si n est.m²/ C (Newton x Square Metro / Coulomb). Alternativement, comme le champ est également mesuré en v / m (volt dans le métro), l'écoulement électrique est en (v ∙ m) m).

Exemples

Selon la définition, le flux électrique peut être positif, négatif ou égal à 0. Le flux de champ électrique est:

Il peut vous servir: aimantation: moment magnétique orbital et spin, exemples

-Positif lorsque l'angle θ entre ET et n Il est inférieur à 90 °, car le cos θ est supérieur à zéro.

-Négatif si cet angle est supérieur à 90 °, car alors cos θ est inférieur à zéro.

-Void lorsque θ vaut exactement 90º, car cos 90º = 0 et que les lignes de champ dans ce cas sont tangentielles à la surface.

-D'un autre côté, si l'angle entre ET et n Il est égal à 0, le débit acquiert sa valeur maximale.

Ces possibilités sont présentées dans l'image suivante:

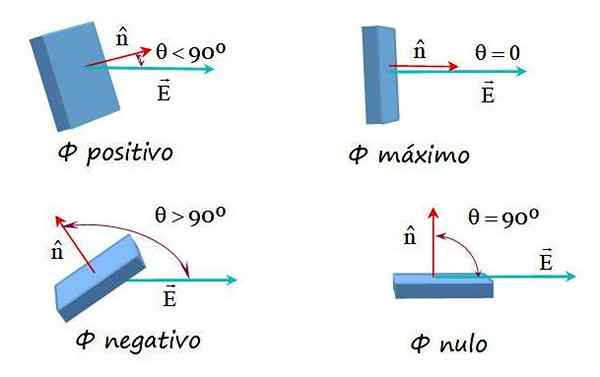Figure 2. Exemples d'écoulement de champ électrique avec diverses orientations entre le champ et le vecteur de surface normal. Source: F. Zapata.

Flux de champ électrique sur une surface arbitraire

Auparavant, l'écoulement de champ électrique a été déterminé dans le cas particulier d'un champ uniforme affectant une surface plate. Pour une surface arbitraire et / ou un champ électrique non uniforme, l'angle entre ET et n peut varier d'un point en point.

Dans la figure suivante, il y a deux exemples, à gauche une surface incurvée et à droite une surface fermée.

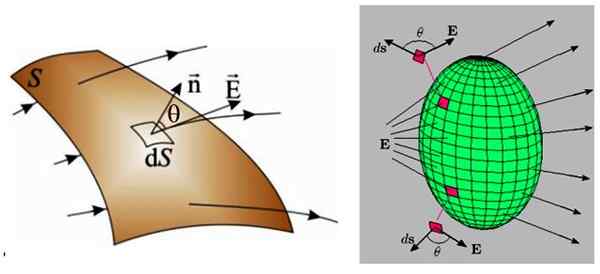figure 3. À gauche une surface arbitraire à travers laquelle un champ électrique non uniforme traverse. À droite, un champ électrique non uniforme traverse une surface fermée, donc l'écoulement net dans ce cas est vide. Source: F. Zapata.

Dans les deux cas, la surface est divisée en régions beaucoup plus petites, de taille infinitésimale, appelée DS, pour laquelle il traverse également un flux infinitésimal Dφ:

dφ = (ET•n) Ds = (ecosθ) ds

Le champ total est obtenu en ajoutant toutes ces contributions infinitésimales:

Le symbole de S comme indice dans l'intégrale indique qu'il doit être calculé sur toute la surface. Si cela est fermé, il est indiqué avec un petit cercle sur l'intégrale:

Peut vous servir: constantes antoine: formules, équations, exemples

Dans le cas des surfaces fermées, n Soulignez toujours, donc le flux a un signe + lorsqu'il est sortant, car l'angle entre ET et n est inférieur à 90 ° et signe - lorsque le champ est entrant, car alors l'angle entre ET et n est supérieur à 90 ° (voir figure 2).

Notez que sur la surface fermée à droite, le nombre de lignes de champ qui entre dans la surface est égale au nombre de lignes qui sortent. Par conséquent, l'écoulement net, défini comme la somme algébrique du flux entrant et du flux sortant, est vide.

La source de champ électrique dans ce cas est en dehors de la surface, cependant, le débit net serait différent de 0 si la source de champ électrique (la distribution des charges) était à l'intérieur de la surface.

Exercices

Exercice 1

Vous avez un champ électrique ET = 3.5 kN / c X et une surface rectangulaire plate de 0.35 m de large par 0.7 m de long. Trouvez le flux de champ électrique qui traverse le rectangle dans les cas suivants:

a) La surface est parallèle au plan yz.

b) Le rectangle est parallèle au plan xy.

c) Le plan normal forme un angle de 40º avec l'axe x et contient l'axe et.

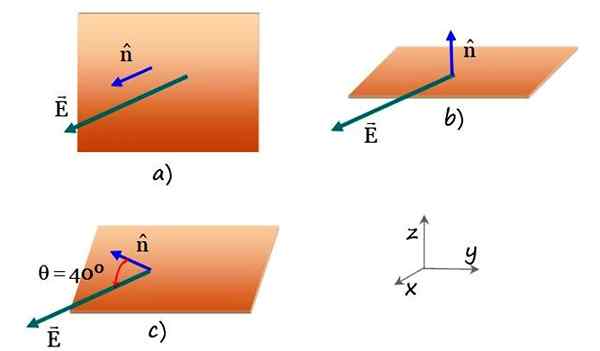Figure 4. Un plan rectangulaire croisé par un champ électrique uniforme dans différentes orientations planes. Source: F. Zapata.

Solution à

Le vecteur normal et le vecteur de champ électrique sont parallèles, donc l'angle θ entre les deux est 0º et l'écoulement électrique est:

Φ = (e ∙ s) cos 0 = e ∙ s

La zone S du rectangle est:

Peut vous servir: méthode parallélogramme: exemples, exercices résolus

S = 0.35 m x 0.7 m = 0.245 m²

Remplacement en φ:

Φ = e ∙ s = 3.5 x 10³ N / C × 0.245 m² = 857.5 N ∙ M² / C.

Solution B

Le flux de champ électrique est 0, car les vecteurs ET et n Ils sont perpendiculaires les uns aux autres.

Solution C

L'angle θ entre le champ ET Et le vecteur normal n est 40º (voir figure) donc:

Φ = e ∙ s ∙ cos θ = 3.5 x 10³ N / C × 0.245 m² × cos 40º = 656.9 N ∙ M² / C.

Exercice 2

Calculez le flux de champ électrique qui produit une charge ponctuelle positive qui_soit = 2 μC situé au centre d'une sphère de rayon r = 5 cm.

Solution

Le champ produit par la charge q_soit Il n'est pas uniforme, mais d'après la loi de Coulomb, on sait qu'à la surface de la sphère, il a une amplitude de:

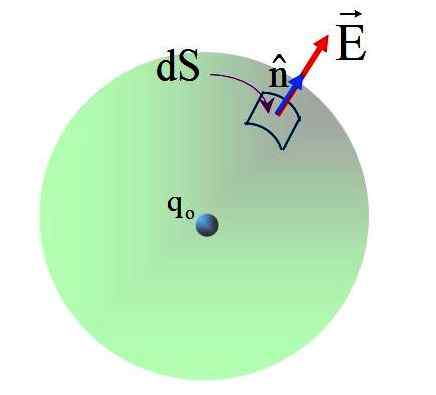Figure 5. Des mouches du champ produites à la surface de la sphère par une charge ponctuelle en son centre. Source: F. Zapata.

Le champ a une direction radiale et le vecteur normal n, Par conséquent, l'angle entre les deux vecteurs est de 0 à tout point de la surface sphérique. Remplacement:

Il faut que:

L'intégrale de DS sur toute la surface sphérique s est la zone de celui-ci, qui est 4πr^2, donc:

Qui conclut que le flux de champ électrique ne dépend pas de la surface, mais de la charge verrouillée dedans.

Sa valeur est:

Φ = 4π × 9 × 10⁹ x 2 × 10^-6 N⋅m²/ C = 2.3 x 10⁵ N⋅m²/ C

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
2. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 5. Électrostatique. Édité par Douglas Figueroa (USB).
3. Giambattista, un. 2010. La physique. 2e. Élégant. McGraw Hill.
4. Giancoli, D.  2006. Physique: principes avec applications. 6e. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1. Pearson.